
математика.зачет
.doc
Программа подготовки к зачету по математике, группы ПЗ-121, 122, П-110-112,
2013-14 учебный год
Тема: «Неопределенный и определенный интегралы»
-
Понятие неопределенного интеграла, его геометрический смысл и его свойства.
-
Методы интегрирования: непосредственное интегрирование, метод замены переменной, метод интегрирования по частям.
-
Таблица интегралов (10 формул).
-
Определенный интеграл. Понятие, геометрический смысл и его свойства.
-
Формула Ньютона-Лейбница.
-
Методы интегрирования определенных интегралов: особенности метода замены переменной, формула метода интегрирования по частям.
-
Приложения определенного интеграла: вычисление площади плоской фигуры.
-
Приложения определенного интеграла: вычисление объема тела вращения.
Тема: «Двойные интегралы»
-
Двойной интеграл: понятие и его свойства.
-
Формула вычисления двойного интеграла через двукратный в декартовой системе координат.
-
Понятие полярной системы координат, формулы связи декартовых координат с полярными.
-
Формула замены переменных в двойном интеграле при переходе к полярной системе координат.
-
Вычисление двойного интеграла через двукратный в полярной системе координат.
-
Вычисление площади плоской фигуры через двойной интеграл.
Тема: « Дифференциальные уравнения»
-
Понятие дифференциального уравнения и его порядка. Примеры дифференциальных уравнений.
-
Дифференциальные уравнения первого порядка. Понятие его общего и частного решений.
-
Постановка задачи Коши для уравнений первого порядка. ЕЕ геометрический смысл.
-
Уравнения с разделяющимися переменными. Понятие и метод интегрирования.
-
Однородные уравнения первого порядка. Понятие и метод интегрирования.
-
Линейные уравнения первого порядка. Понятие и метод интегрирования. Уравнение Бернулли.
-
Понятия дифференциального уравнения второго порядка, его общего и частного решений.
-
Постановка задачи Коши для уравнения второго порядка.
-
Дифференциальные уравнения второго порядка, допускающие понижение порядка (3 типа).
-
Линейные однородные уравнения второго порядка с постоянными коэффициентами. Построение общего решения по корням характеристического уравнения.
-
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. Структура общего решения. Построение частного решения по правой части (2 случая).
Примечание:
Каждый вариант зачетного билета содержит 6 задач (из разных тем программы).
Образец зачетного билета
Вычислить интегралы 1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Найти объём тела, образованного
вращением кривой
![]() ,
,
![]() вокруг оси
вокруг оси
![]() .
.
Решить дифференциальные уравнения:
1)![]() .
2)
.
2)![]() .
.
Задачи программы – минимум для зачета
( ПЗ-121, 122; П-110-112)
Найти интегралы:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.
![]() .
8.
.
8.
![]() .
.
Вычислить определенные интегралы:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
5.
.
5.
![]() .
.
Найти общее решение дифференциального уравнения:
-
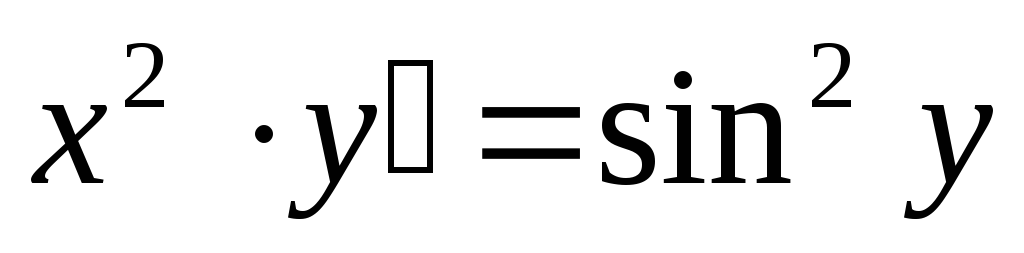 .
2.
.
2.
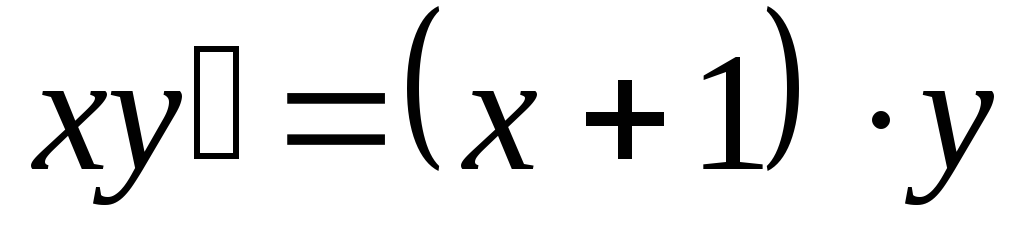 .
3.
.
3.
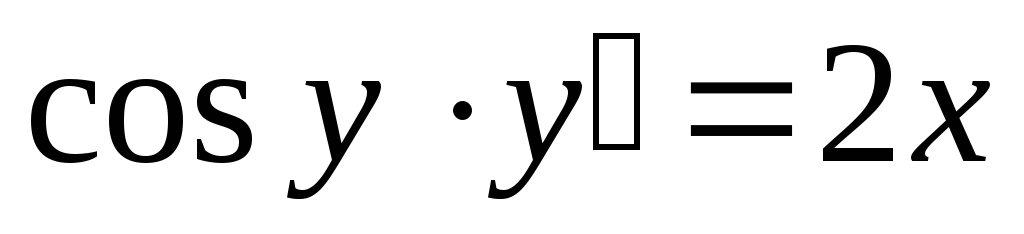 .
.
4.
![]() .
5.
.
5.![]() .
6.
.
6.![]() .
.
7.
![]() .
8.
.
8.![]() .
9.
.
9.![]() .
.
Вычислить площадь фигуры:
1. Вычислить
площадь фигуры, ограниченной параболой
![]() ,
прямыми
,
прямыми
![]() и осью абсцисс.
и осью абсцисс.
2. Вычислить
площадь фигуры, ограниченной параболой
![]() и прямой
и прямой
![]() .
.
Вычислить двойной интеграл:
1.
![]() ,
где
,
где![]() - область, ограниченная линиями:
- область, ограниченная линиями:
![]() .
.
2.
![]() ,
где
,
где![]() - область, ограниченная линиями:
- область, ограниченная линиями: ![]() .
.
3.
![]() ,
где
,
где![]() -область,
ограниченная линиями:
-область,
ограниченная линиями:
![]() .
.
4.
![]() ,
где
,
где ![]() - полукруг:
- полукруг: ![]()
5.
![]() ,
где
,
где ![]() - часть кольца:
- часть кольца: 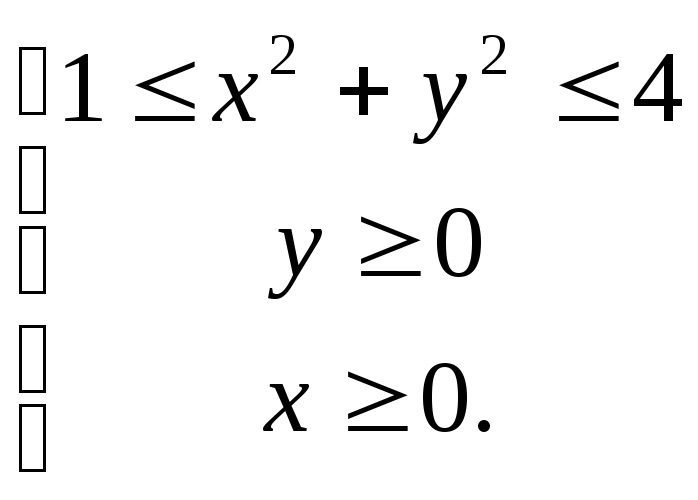
6.
![]() ,
где
,
где ![]() - часть кольца:
- часть кольца: ![]()
