Тесты по теме №1

1. Дан треугольник АВС с вершинами А(0;0), В(4;3), С(12;5). Определить точку Д(x;y) пересечения биссектрисы внутреннего угла А с противолежащей стороной ВС.

R

£

£

2. Найти площадь треугольника с вершинами А(7,3,4), В(1,0,6), С(4,5,-2).

R

£

£

3. Найти неизвестный элемент х: .

£ 1;

£– 2;

£0;

R – 1;

£2.

4. Найти неизвестный элемент х:

.

£ 6;

£ 2;

£ – 3;

R – 6;

£ – 12.

5. Вычислить произведение матриц:

R

£

£

6. Найти элемент матрицы АВ, если:

£ = 32

R = 49

£= 71

7. Вычислить минор элемента аматрицы третьего порядка.

£ а= 1

£ а= 27

Rа= -19

8. Вычислить определитель матрицы

£12

R40

£56

9. Вычислить определитель матрицы

R160

£238

£420

10. Вычислить минор элемента матрицы третьего порядка:

£41

R- 41

£47

11. Вычислить определитель матрицы .

R – 7;

£ 9;

£ 16;

£ 7;

12. Минор m₂₁ получается

£вычеркиванием первой строки и второго столбца определителя.

R вычеркиванием второй строки и первого столбца определителя.

£ вычеркиванием первой строки и второго столбца матрицы.

£ вычеркиванием второй строки и первого столбца матрицы.

13. Вычислить минор m₁₂ определителя .

£ – 7;

£ 4;

£ 3;

R 7;

£ – 3.

14. Обратной матрицей обладают

£ все матрицы;

£ все квадратные матрицы;

Rневырожденные квадратные матрицы;

£ вырожденные квадратные матрицы.

15. Векторное произведение двух векторов – это вектор, который

£ находится в одной плоскости с этими векторами;

£ коллинеарен с этими векторами;

£ с этими векторами составляет компланарную тройку;

R перпендикулярен этим векторам;

£параллелен этим векторам.

16. Выражение 2 + 3i, где i – мнимая единица,

£ действительное число;

£рациональное число;

R комплексное число;

£ иррациональное число.

17. Найти сумму комплексных чисел 1 + 2i и 2 – i.

£ 3 –i;

R 3 +i;

£ 2 –2i;

£ 4 –3i.

18.Определитель 3 2 равен 0 при в = …

6 5в-1

£ 2

R 1

£ 0

19. В треугольнике оав даны векторы. Найти векторы ма и мв, где м – середина стороны ав.

£

£

R

20. Вычислить определитель третьего порядка:

£2.

R4.

£6.

£3.

21. Вычислить определитель треугольной матрицы:

£20.

£15.

R-15.

£3.

22.Прямая проходит через точки 0(0;0) и В(12;3). Тогда её угловой коэффициент равен

£ 4

R

£

£ 7

23. Совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется

£квадратной матрицей;

Rпрямоугольной матрицей;

£вектором-строкой;

£вектором-столбцом;

£определителем.

24. Порядком квадратной матрицы n ´ n называется

Rn²

£n

£матрица не имеет порядка.

25. Порядком прямоугольной матрицы n ´ m называется

£n;

£m.

Rматрица не имеет порядка.

26. Найти неизвестный элемент х: .

£1

£– 2

£0

R– 1

£2.

27. Найти неизвестный элемент х:

.

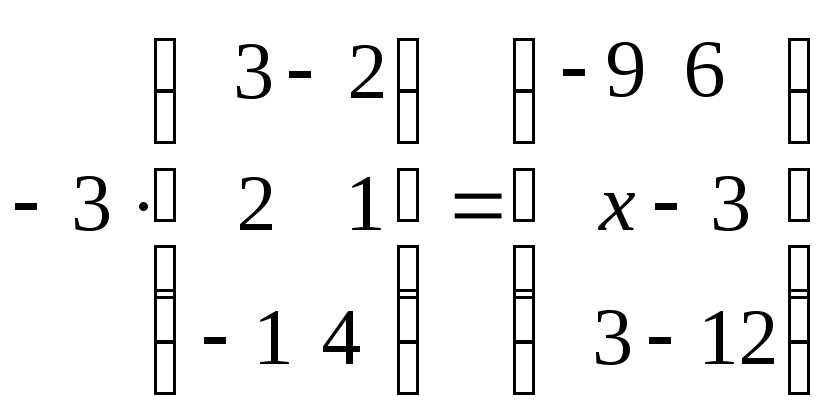£6;

£2;

£– 3;

R– 6;

£– 12.

28. Найти неизвестный элемент х:

.

£0;

R– 4;

£6;

£– 8;

£4.

29. Найти неверный ответ.

£Определитель не изменится, если его строки заменить столбцами.

£Определитель не изменится, если к элементам одного ряда прибавить соответствующие

£элементы параллельного ряда, умноженные на любое число.

RОпределитель не изменится, если заменить первый столбец вторым столбцом.

£Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.

30. Ранг матрицы размерности n ´ m

£ равен min(m, n);

£ равен max(m, n);

R не превышает min(m, n);

£ равен порядку матрицы.

31. Найти ранг матрицы .

£ 1

R 2

£ 3.