§1.3. Определители и их свойства

Определители

Определителем (детерминантом) квадратной матрицы n-го порядка называется число

.

þ Обозначения: detA,  и |A|.

Строки и столбцы определителя называются рядами.

Определитель второго порядка вычисляется по правилу (1):

. (1)

Определитель третьего порядка вычисляется по правилу 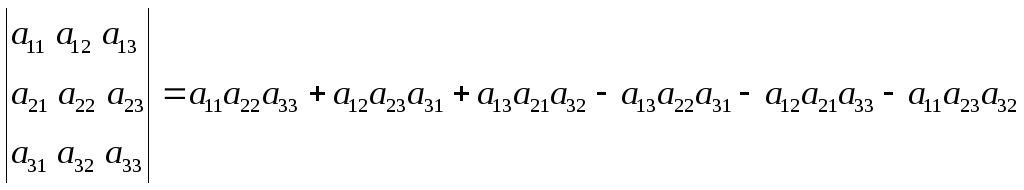(2):

(2).

Правило вычисления определителя третьего порядка следующее. Это алгебраическая сумма шести тройных произведений элементов, стоящих в разных строках и разных столбцах. Со знаком плюс берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали. Со знаком минус берутся произведения, сомножители которых стоят на другой диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (рис. 1).

(+) (-)

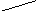
Рис. 1. Правило вычисления определителя третьего порядка

@ Задача 1. Найти .

Решение: Определитель второго порядка вычисляется по правилу (1): detA = 2·3 – (–3)·4=18.

@ Задача 2. Найти .

Решение: Определитель третьего порядка вычисляется по правилу (2):

detA = 1·3·2 + 2·1·0 + 3·2·1 – 3·3·0 – 2·2·2 – 1·1·1 = 3.

Минор и алгебраическое дополнение

Минором m_ij некоторого элемента a_ij определителя n–го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя путем вычеркивания i-й строки и j-го столбца, на пересечениях которых находится выбранный элемент.

Например, минором элемента a₁₁ определителя третьего порядка является .

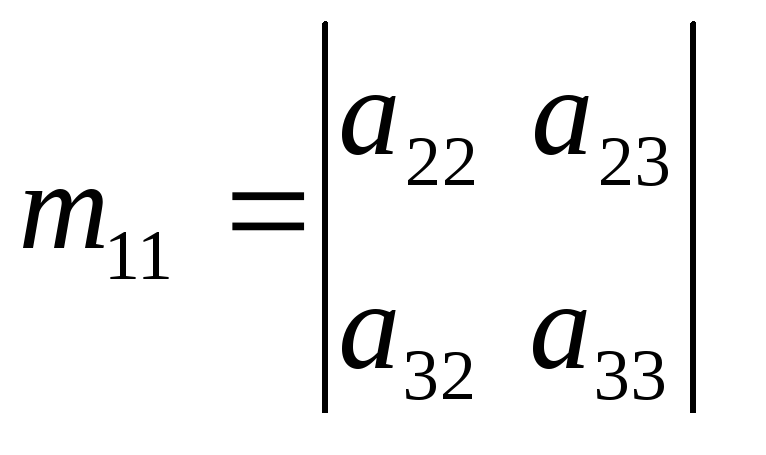Алгебраическим дополнением называется A_ij = (– 1)^i+j m_ij. Если сумма индексов алгебраического дополнения i + j четное число, то алгебраические дополнения и миноры совпадают: A_ij = m_ij, а если – нечетное число, то они отличаются знаком: A_ij = – m_ij.

Свойства определителей

1. Если какой-то ряд состоит из одних нулей, то определитель равен 0.

2. Определитель не изменится, если его строки заменить столбцами, и наоборот.

3. При перестановке двух параллельных рядов определитель меняет знак.

4. Определитель, имеющий два одинаковых ряда, равен нулю.

5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

6. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух определителей, с соответствующими слагаемыми этой суммы.

7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

8. Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.

Например, определитель третьего порядка равен:

detA = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ = a₁₁m₁₁ – a₁₂m₁₂ + a₁₃m₁₃ . (3)

@ Задача 3. Найти .

Решение: Определитель найдем, применяя формулу (3):

Ранг матрицы

Наибольший порядок отличных от нуля детерминантов (миноров) прямоугольной матрицы m  n, называется рангом матрицы r, причем r  min(m, n). Для квадратной матрицы ранг r  n.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.

@ Задача 4. Найти ранг матрицы размерности3  4.

Решение: Ранг матрицы r  min(3, 4) = 3. Все детерминанты третьего порядка равны нулю, так как две их строки (вторая и третья) одинаковые (отличаются на постоянный множитель). Отличны от нуля только детерминанты второго порядка, поэтому r = 2.