Николаев в.С.

«МАТЕМАТИКА»

Москва 2009

Содержание

Введение………………………………………………………………..

Тема 1 Операции над векторами и матрицами 4

Тема 2 Системы линейных алгебраических уравнений 36

Тема 3 Математический анализ и дифференциальные уравнения 42

Тема 4 Неопределенный интеграл 74

Тема 5 Определенный интеграл 81

Тема 6 Теория вероятностей и математическая статистика 89

Тема 7 Экономико-математические методы 114

Тема 8 Экономико-математические модели 176

Заключение………………………………………………………………

Литература……………………………………………………………….

ВВЕДЕНИЕ

В учебном пособии представлен краткий курс высший математики, который будет полезен студентам, не математического профиля (ЕН Ф.01). В пособии изложены основные понятия, формулы и методы высшей математики, представлены решения типичных задач, предложены задачи и тестовые задания для самостоятельной работы и проверки своих знаний, которые будет полезны и при сдаче зачетов и экзаменов, а также представлены варианты для контрольных работ.

Учебное пособие написано в соответствии с требованиями государственных стандартов высшего образования по высшей математике для экономических специальностей. В программу высшей математики входят линейная алгебра с элементами аналитической геометрии, дифференциальное и интегральное исчисления, ряды, дифференциальные уравнения, теория вероятностей и математическая статистика и экономико-математические модели.

Во все темы учебного пособия вошли основные понятия, определения, методы расчетов и решения типовых задач. В связи с тем, что экономистам в основном нужно знать приложения высшей математики в экономике, акцент ставится на таких примерах, задачах, моделей, которые имеют интерес с точки зрения экономической науки. Такие задачи есть во всех темах.

Студентам предлагается прочесть теоретическую часть каждой темы, обращая внимание на определения, свойства, описание методов расчета, решения задач и попытаться самостоятельно решить представленные в соответствующем параграфе задачи.

Тема №1 Операции над векторами и матрицами

§1.1Матрицы

Любая статистическая таблица это пример матрицы. Таковой является, например следующая таблица:

Производство деталей за смену

Детали, шт.	Бригады
	I	II
А	25	35
Б	30	50
В	60	100

Совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов, называется прямоугольной матрицей размерности m  n.

þ Обозначения: Матрицы обозначаются прописными латинскими буквами A, B, C; элементы матрицы обозначаются строчными латинскими буквами, например, a_ij, i = 1,2,…m; j = 1,2,…n, где i показывает номер строки, j - номер столбца матрицы. Другими словами элемент матрицы a_ij - это элемент, находящийся на пересечении i–ой строки и j–ого столбца матрицы.

Общий вид прямоугольной матрицы записывается как

.

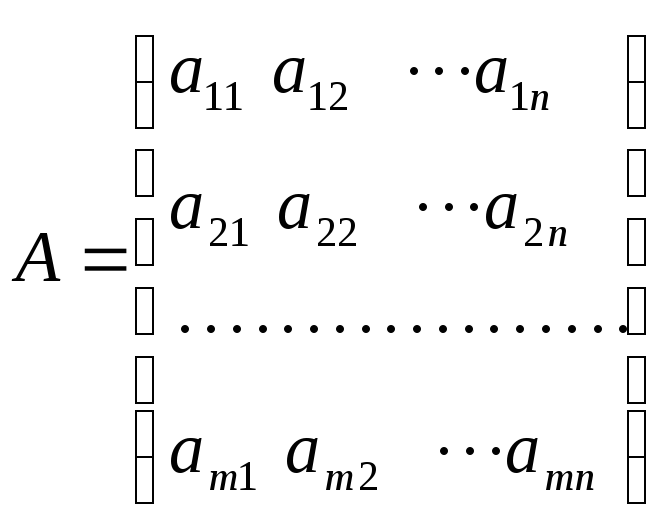Матрица называется квадратной матрицей порядка n, если число строк m равно числу столбцов n.

При m = 1 матрица содержит одну строку и называется вектором-строкой. При n = 1 матрица содержит один столбец и называется вектором-столбцом. Элементы вектора называются также компонентами или координатами вектора.

Если все элементы прямоугольной матрицы нули (a_ij = 0), то матрица называется нулевой матрицей и обозначается буквой 0.

Если в квадратной матрице элементы главной диагонали равны единице (a_ii = 1), а все остальные элементы – нули (a_ij = 0, i¹j), то матрица называется единичной матрицей и обозначается как E.

Матрицы A и B равны, если равны все соответствующие элементы этих матриц a_ij = b_ij.