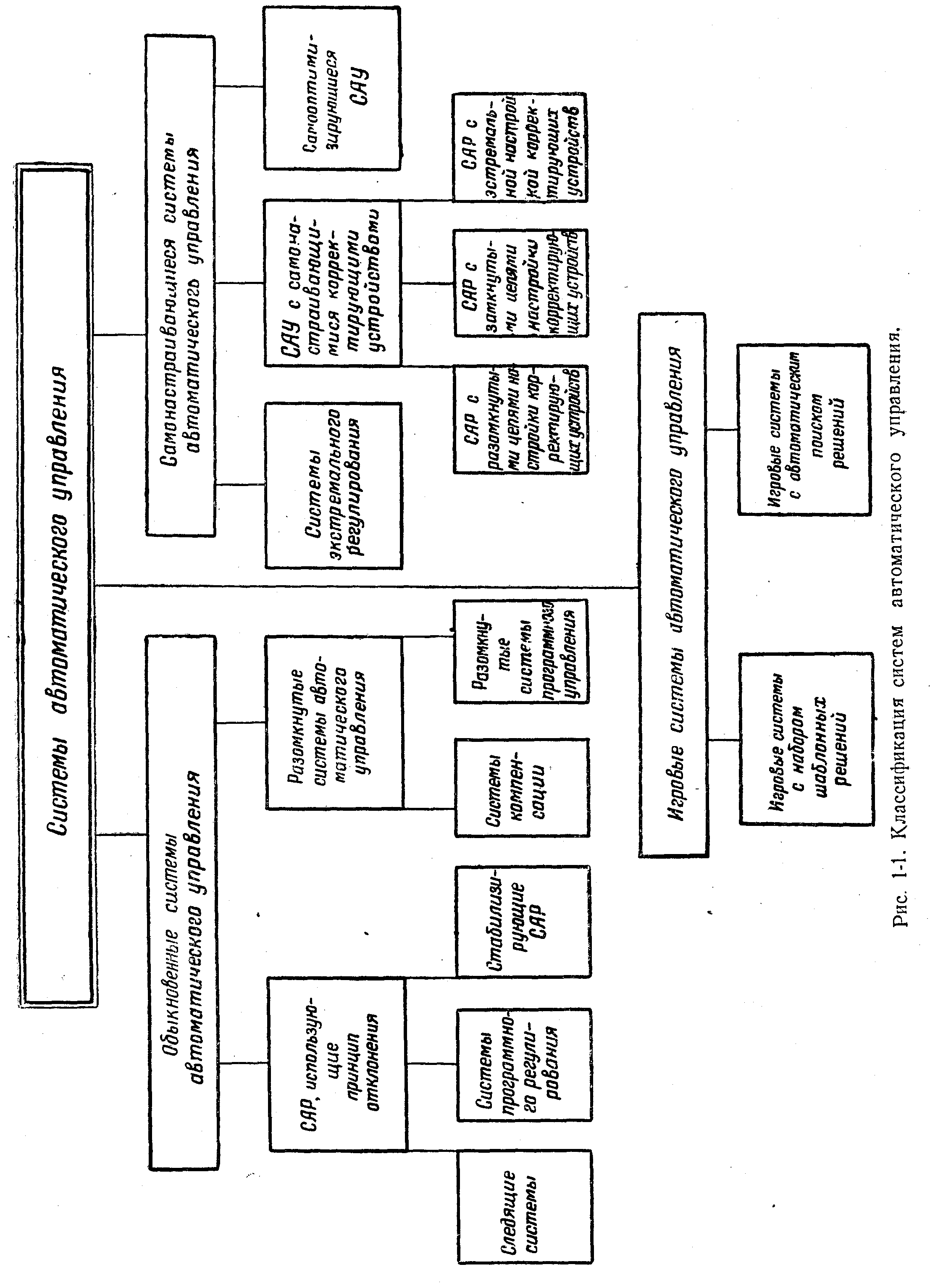
2. Классификация систем автоматического управления.

Классификация систем по виду начальной и рабочей информации.

Дать подробную законченную классификацию систем автоматического управления практически невозможно.

С точки зрения общности классификации систем автоматического управления наиболее удобным классификационным признаком является используемая информация об управляемом процессе или системе.

Информация – любая совокупность сведений, первичным источником которых является опыт.

При классификации систем автоматического управления следует различать два вида информации: начальную или априорную информацию и рабочую информацию.

Необходимой начальной или априорной информацией назовём совокупность сведений об управляемом процессе или системе, необходимых для построения и функционирования данной системы автоматического управления рассматриваемым процессом и имеющихся в нашем распоряжении до начала функционирования системы.

Рабочей информацией называется совокупность сведений о состоянии процесса, используемых в самом процессе.

Рабочая информация передаётся в виде сигналов – физических процессов, несущих информацию.

Обыкновенные (несамонастраивающиеся) системы автоматического управления – системы, требующие для построения и функционирования наибольшей (полной) начальной информации.

Самонастраивающиеся системы автоматического управления – системы, не требующие для своего построения и функционирования полной начальной информации об управляемом процессе.

Перед самонастраивающимися (адаптивными) системами ставятся следующие задачи:

1. Поддержание режима, близкого к оптимальному (наилучшему) – автоматические оптимизаторы или экстремальные регуляторы.

2. Поддержание оптимальной работы системы по условию максимального быстродействия.

При этом различают:

1. Системы с самонастройкой программы (экстремальные системы).

2. Системы с самонастройкой параметров (собственно самонастраивающиеся системы).

3. Системы с самонастройкой структуры (самоорганизующиеся системы).

Сложные задачи управления операциями над многими объектами можно трактовать как задачи автоматического проведения некоторой игры. Действия сторон могут быть частично случайными, частично подчинёнными некоторым правилам – алгоритмам.

Игра состоит из ряда последовательных этапов- шагов.

Основной особенностью принципа действия игровых систем является формирование команд управления на основе сопоставления множества возможных решений – выборов на каждом этапе управляемой операции. Критерием сопоставления различных возможных решений-выборов служит некоторый показатель, именуемый функцией выгоды.

Классификация систем автоматического регулирования по виду оператора

системы.

Математическая модель системы управления — это пара "оператор системы и модель внешних воздействий". Оператором системы называется закон, в соот­ветствии с которым система преобразует внешнее (входное) воздействие g в вы­ходной сигнал х (рис. В.4).

Оператор системы. Функция, которая любому значению аргумента x ставит в соответствие некоторый элемент y множества Y, не являющегося множеством чисел, называется оператором. Под понятием оператора объединяются любые математические действия: все алгебраические действия, дифференцирование, интегрирование, сдвиг во времени, решение дифференциальных, интегральных, алгебраических и любых других функциональных уравнений, а также любые логические действия. Задать оператор системы – это значит задать совокупность (программу) действий, которые надо осуществить над входной функцией, чтобы получить выходную функцию.

Рис. В.4

По виду оператора системы управления делятся на:

а) линейные и нелинейные;

б) непрерывные, дискретные, непрерывно-дискретные;

в) нестационарные и стационарные;

г) детерминированные и стохастические;

д) одномерные и многомерные;

е) с сосредоточенными и с распределенными параметрами.

Внешние воздействия делятся на:

а) непрерывные (функции непрерывного аргумента) и дискретные (функции дискретного аргумента);

б) детерминированные и случайные;

в) одномерные и многомерные.

Чтобы классифицировать конкретную систему, нужно указать на шесть классов, к которым принадлежит оператор системы, и на три класса, к которым принадлежат внешние воздействия. Например, она может оказаться линейной непрерывно-дискретной нестационарной детерминированной одномерной с со­средоточенными параметрами при непрерывных случайных одномерных внеш­них воздействиях.

Поясним названия классов операторов на примере описания систем диф­ференциальными или разностными уравнениями. Линейные системы описыва­ются линейными дифференциальными уравнениями, нелинейные — нелинейны­ми дифференциальными уравнениями. Непрерывные системы описываются дифференциальными уравнениями; дискретные — разностными; непрерывно-дискретные — дифференциально-разностными уравнениями. Нестационарные системы описываются уравнениями с переменными коэффициентами, стацио­нарные — уравнениями с постоянными коэффициентами. Детерминированные системы описываются уравнениями, коэффициенты которых являются детерми­нированными величинами или функциями времени, стохастические — стохас­тическими уравнениями. Одномерные системы имеют один вход и один выход, многомерные системы имеют суммарное число входов и выходов, большее двух. Наконец, системы с сосредоточенными параметрами описываются обыкновен­ными дифференциальными уравнениями, с распределенными параметрами — уравнениями в частных производных.