ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ (ИАТЭ)

ФАКУЛЬТЕТ КИБЕРНЕТИКИ

О.М. ГУЛИНА

ПРИНЯТИЕ РЕШЕНИЙ

В УСЛОВИЯХ НЕЧЕТКОЙ ИНФОРМАЦИИ

учебное пособие по курсу

«Теория принятия решений»

ОБНИНСК 2008

УДК 519.816

Гулина О.М. Принятие решений в условиях нечеткой информации: Учебное пособие по курсу «Теория принятия решений».

Пособие содержит материалы для самостоятельного изучения современного математического аппарата, имеющего важные приложения в области техники, экономики и управления Рассматривается методология принятия решений в условиях плохо определенной информации, характерной для этапа проектирования. Теоретический материал выдержан в едином методическом плане, направлен на использование формальных процедур объединения разнородной информации, адекватного описания факторов, критериев, параметров на этапе проектирования. Приведены примеры практических ситуаций с подробными пояснениями и решениями.

для студентов специальностей ВТ, АСОИУ, Информационные системы, направления ИВТ всех форм обучения

Введение

Традиционно для принятия решений в условиях неопределенности, в которых функционирует практически любое предприятие, специалистами по теории управления рекомендуется использовать вероятностно-статистические методы. Однако при этом возникают определенные трудности в интерпретации полученных решений, к тому же некоторые из этих методов чувствительны к отклонениям от принятых при построении модели допущений.

Одна из основных целей построения математических моделей ре­альных систем – найти способ обработки имеющейся информации для выбора рациональных вариантов управления системой. Очень часто, и особенно при исследовании экономических, социальных и других систем, в функционировании которых участвует человек, значитель­ное количество информации о системе может быть получено от людей, имеющих опыт работы с данной системой и знающих ее особенности, имеющих представление о целях функционирования системы, и т.п. Эта информация носит субъективный характер и ее представ­ление в естественном языке, как правило, содержит большое число неопределенностей типа «много», «мало», «сильно увеличить», «вы­сокий», «очень эффективный» и т.п., которые не имеют аналогов в языке традиционной математики. Поэтому и описание подобной инфор­мации на языке традиционной математики обедняет математическую модель исследуемой реальной системы и делает ее слишком грубой. Вместе с тем наличие математических средств отражения нечеткости исходной информации позволяет построить модель, более адекватную реальности.

Одним из начальных шагов на этом пути считается направление, связанное с именем видного американского математика Леона Заде и по­лучившее название теории нечетких множеств (Fuzzy sets). Лежащее в основе этой теории понятие нечеткого множества предла­гается в качестве средства математического моделирования неопреде­ленных понятий, которыми оперирует человек при описании своих представлений о реальной системе, своих целей, предпочтений и т.п. Нечеткое множество – это математическая модель класса с нечеткими, или размытыми границами. В этом понятии учитывается воз­можность постепенного перехода от принадлежности к непринадлежнос­ти элемента множеству. Элемент может, вообще говоря, иметь степень принадлежности множеству, промежуточную между полной принадлежностью и полной непринадлежностью.

Одним из важных направлений применения этого нового подхода является проблема принятия решений при нечеткой исходной информа­ции. Здесь появляется возможность сузить множество возможных альтернатив, отбросив те из них, для которых имеются заведомо более приемлемые варианты, подобно тому, как это делается при использовании принципа Парето.

Теория нечетких множеств – раздел прикладной математики, посвященный методам анализа неопределенных данных, в которых описание неопределенностей реальных явлений и процессов проводится с помощью понятия множества, не имеющего четких границ. Теория нечетких множеств – это расширение классической теории множеств.

Основанные на этой теории различные компьютерные системы существенно расширяют область применения нечеткой логики. В настоящее время наибольший интерес с точки зрения результативности вызывает приложение аппарата нечетких множеств в области нечеткого управления.

Методами нечеткой логики в сфере бизнеса можно решать такие задачи, как:

• управление финансовыми и информационными потоками;

• оценка инвестиционных проектов и идей по развитию бизнеса, риска различных бизнес-планов и их прибыльности;

• прогноз поведения цен и оптимальных стратегий валютных операций, ценных бумаг, недвижимости и т.д.

За рубежом в составе компаний, занимающихся аудитом и консалтингом, есть отделы информационных технологий, профессионально изучающие программные продукты с дальнейшей рекомендацией их заказчику. К сожалению, в России разработка информационных систем управления предприятием развита достаточно слабо: на современном рынке практически отсутствуют российские аналоги. Изменить сложившуюся ситуацию представляется возможным за счет изменения, прежде всего, методологии проектирования таких систем, учитывающей неопределенность информации и сложность применения общепринятых количественных методов даже на этапе анализа предметной области. Непосредственно использование алгоритмов нечеткой логики в приложениях – явление довольно редкое, хотя в последнее время они широко используются при создании экспертных систем, систем-классификаторов (classifiers) при исследовании критических и рисковых ситуаций, для распознавания образов и т.д.

На Западе все большие средства вкладываются в развитие приложений, при создании которых используются именно объектно-ориентированные методики проектирования (Сoad/Yordon, Shlaer/Mellor, Rumbaugh, Jacobson, Booch, объединенный Fuzzy-метод). «Чистый» объектный подход уже на ранних стадиях требует представления данных о классификации в виде диаграмм классов, что не всегда возможно в случае сложных систем, характеризующихся высоким уровнем неопределенности, без проведения тщательного анализа объектов предметной области. Например, при применении такого метода классификации как концептуальная кластеризация, где трудно однозначно определить принадлежность элемента к той или иной категории, применение аппарата нечетких множеств позволяет оценить наиболее вероятное нахождение данного объекта в рамках определенного класса. А как еще можно оценить, например, значение атрибутов «быстрее-медленнее» для роста цен, «высокая-низкая» пропускная способность при проектировании сетей и т.д.?

В сфере маркетинга предоставляется возможность узнавать характер потребностей различных категорий клиентов, исследовать временные шаблоны: например, через какое время клиенты, которые приобрели компьютеры, будут приобретать соответствующее программное обеспечение, – производить анализ покупательской корзины и т.п.

Широкой областью внедрения является финансовый анализ (рынок ценных бумаг), исследование хранилищ данных.

При обработке SQL-запроса также часто встречается ситуация, когда либо сложно получить ответ, в точности соответствующий запросу, либо, наоборот, может быть получен слишком большой объем данных. При встраивании нечеткой логики в SQL-запрос можно получить информацию, в некотором приближении удовлетворяющую заданным критериям, путем задания соответствующих диапазонов числовых величин (например, получение объемов продаж).

Развитие приложений, реализующих нечеткую логику, происходило и на аппаратном уровне. В 1986 году в AT&T Bell Labs создавались процессоры с “прошитой” нечеткой логикой обработки информации. В Европе и США ведутся интенсивные работы по интеграции fuzzy-команд в ассемблеры промышленных контроллеров встроенных устройств (чипы Motorola 68HC11.12.21). Кроме того, разрабатываются различные варианты fuzzy-сопроцессоров, которые контактируют с ЦП через общую шину данных, концентрируя свои усилия на размывании/уплотнении информации и оптимизации использования правил (продукты Siemens Nixdorf). И все же по проведенным анализам стоимости продукции дешевле эмулировать нечеткую логику, хотя сложным вопросом является трансляция fuzzy-системы на традиционный язык программирования. Компания Aptronix предлагает использовать язык Java, имеющий все необходимое для вполне адекватного воспроизведения инструкций нечеткой логики приложения. Кроме того, использование Java API открывает новые перспективы для исследования fuzzy-систем во взаимодействии. Internet, как глобальная среда распространения Java-приложений, идеально подходит для интеграции прикладных устройств, созданных при помощи алгоритмов нечеткой логики.

Широкие возможности по программированию бизнес–логики и обработки данных дает включение JavaBeans и Java-сервлетов в комплекты разработчика приложений; это обеспечивает независимость от клиентской операционной системы и пользовательского интерфейса.

В перспективе достижимы следующие области использования приложений с нечеткой логикой в Internet:

• диагностика и восстановление сетевых конфигураций и управление производственными объектами;

• удаленный мониторинг устройств и организация распределенных вычислений;

• всевозможные портативные гиды, доски объявлений с динамически изменяющимися свойствами и гибкой функциональностью;

• интеллектуальные поисковые машины, распределенные системы загрузки и выделения данных.

Развитие теоретической базы и средств моделирования, расширение областей применения, коммерческий успех и распространение fuzzy-приложений расширит возможности классического математического моделирования и обеспечит спрос на специалистов, владеющих соответствующими технологиями.

1 Принятие решений в условиях нечеткой информации

1.1 Идея нечеткого представления информации

При анализе параметров конкретной системы, особенно на этапе проектирования, часто используют понятия, которые имеют нечеткий смысл с точки зрения классической математики: «высокая пропускная способность», «небольшие затраты», «удовлетворительное состояние» и т.д.

Язык традиционной математики, опирающейся на теорию множеств и двузначную логику, недостаточно гибок для моделирования реаль­ных сложных систем, поскольку в нем нет средств для достаточно адек­ватного описания понятий, которыми пользуется человек, и которые имеют неопределенный смысл.

Врачу для установления диагноза незачем знать числовое значение температуры тела больного – 36.6, 38.9 и т.д. Достаточно выразить показания термометра диапазонами (категориями), о которых медики договорились заранее – температура «пониженная», «нормальная», «повышенная», «высокая», «очень высокая» («жар»). Границы этих оценок, естественно, размыты, нечетки, туманны – “пушисты”. Это определяется не только современными представлениями теории нечетких множеств (ТНМ), но и погрешностью самого термометра, методикой измерения температуры и др. Даже параметры больного, выраженные не в вещественном, а в булевом виде (реакция Вассермана, наличие палочки Коха, анализ на СПИД и т.д.), имеют «пушистые» границы. Если заглянуть в любой справочник терапевта, где описаны симптомы болезней, то, как правило, конкретных чисел (температура тела, артериальное давление, содержание гемоглобина в крови и т.д.) там не увидишь. Одни слова – повышено, понижено и т.д. Программы выставления диагноза по введенным в компьютер параметрам больного не получили широкого практического применения. Одна из трудностей в этом деле – перевод параметра (числа) в симптом (категорию).

Стоит нам что-то пересчитать, как мы вступаем с этой пересчитанной субстанцией в глубокий конфликт. Природа не любит не только острых углов, но и счёта, который в ряде случаев просто убивает ее. Это можно наблюдать не только в биологии и физике, где инструменты познания часто неузнаваемо портят сам объект исследования, но и в computer science.

Одна из основных проблем при построении математических моделей ре­альных систем - найти способ обработки имеющейся информации для постановки и решения задачи выбора рациональных вариантов управления системой. Очень часто при исследовании систем значитель­ное количество информации об этой системе может быть получено от людей, имеющих опыт работы с ней и знающих ее особенности, т.е. от экспертов. Эта информация носит субъективный характер и ее представ­ление в естественном языке, как правило, содержит большое число неопределенностей типа «много», «сильно увеличить», «очень эффективный» и т.п., которые не имеют аналогов в языке традиционной математики. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, более адекватную реальности.

Математическая теория, лежащая в основе этого направления, связана с именем видного американского математика Леона Заде и по­лучилае название теории нечетких множеств (Fuzzy sets). Сформулированное им понятие нечеткого множества предла­гается в качестве средства математического моделирования неопреде­ленных понятий.

Нечеткое множество – это математическая модель класса с нечеткими или, иначе, размытыми границами.

Одним из важных направлений применения этого нового подхода является проблема принятия решений при нечеткой исходной информа­ции. Здесь появляется возможность сузить множество возможных ва­риантов, отбросив те из них, для которых имеются заведомо более приемлемые варианты (доминирующие), подобно тому, как это делается при использовании принципа Парето.

2. Понятие нечеткого множества

По традиции четкие множества принято иллюстрировать кругами с резко оконтуренными границами. Нечеткие же множества – это круги, образованные отдельными точками: в центре круга точек много, а ближе к периферии их густота уменьшается до нуля; круг как бы растушевывается на краях. Такие «нечеткие множества» можно увидеть... в тире – на стене, куда вывешиваются мишени. Следы от пуль образуют случайные множества, математика которых известна. Оказалось, что для оперирования нечеткими множествами годится уже давно разработанный аппарат случайных множеств...

Понятие нечеткого множества – попытка математической формализации нечеткой информации с целью ее использования при построении математических моделей сложных систем. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать данному множеству с различной степенью.

Один из простейших способов математического описания нечеткого множества – характеризация степени принадлежности элемента множеству числом, например, из интервала [0,1]. Пусть Х – некоторое множество элементов. В дальнейшем мы будем рассматривать подмножества этого множества.

Нечетким множеством А в Х называется совокупность пар вида (x, _A(x)), где xX, а _А – функция x [0,1], называемая функцией принадлежности (membership function) нечеткого множества А. Значение _A(x) этой функции для конкретного x называется степенью принадлежности этого элемента нечеткому множеству А.

Как видно из этого определения, нечеткое множество вполне описывается своей функцией принадлежности, поэтому мы часто будем использовать эту функцию как обозначение нечеткого множества.

Обычные множества составляют подкласс класса нечетких множеств. Действительно, функцией принадлежности обычного множества BX является его характеристическая функция: _В(x)=1, если xB и _В(x)=0, если xB. Тогда в соответствии с определением нечеткого множества обычное множество В можно также определить как совокупность пар вида (x, _В(x)). Таким образом, нечеткое множество представляет собой более широкое понятие, чем обычное множество, в том смысле, что функция принадлежности нечеткого множества может быть, вообще говоря, произвольной функцией или даже произвольным отображением.

Мы говорим нечеткое множество. А множество чего Если быть последовательным, то приходится констатировать, что элементом нечеткого множества оказывается... новое нечеткое множество новых нечетких множеств и т.д. Обратимся к классическому примеру – к куче зерна. Элементом этого нечеткого множества будет миллион зерен, например. Но миллион зерен это никакой не четкий элемент, а новое нечеткое множество. Ведь считая зерна (вручную или автоматически), немудрено и ошибиться – принять за миллион 999 997 зерен, например. Тут можно сказать, что элемент 999 997 имеет значение функции принадлежности к множеству “миллион”, равное 0.999997. Кроме того, само зерно – это опять же не элемент, а новое нечеткое множество: есть полноценное зерно, а есть два сросшихся зерна, недоразвитое зерно или просто шелуха. Считая зерна, человек должен какие-то отбраковывать, принимать два зерна за одно, а в другом случае одно зерно за два. Нечеткое множество не так-то просто запихнуть в цифровой компьютер с классическими языками: элементами массива (вектора) должны быть новые массивы массивов (вложенные вектора и матрицы, если говорить о Mathcad). Классическая математика четких множеств (теория чисел, арифметика и т.д.) – это крюк, с помощью которого человек разумный фиксирует (детерминирует) себя в скользком и нечетком окружающем мире. А крюк, как известно, – инструмент довольно грубый, нередко портящий то, за что им цепляются. Термины, отображающие нечеткие множества – «много», «слегка», «чуть-чуть» и т.д. и т.п., – трудно «запихнуть» в компьютер еще и потому, что они контекстно зависимы. Одно дело сказать «Дай мне немного семечек» человеку, у которого стакан семечек, а другое дело – человеку, сидящему за рулем грузовика с семечками.

Нечеткое подмножество А множества Х характеризуется функцией принадлежности _A: Х→[0;1], которая ставит в соответствие каждому элементу xX число _A(x) из интервала [0; 1], характеризующее степень принадлежности элемента х подмножеству А. Причем 0 и 1 представляют соответственно низшую и высшую степень принадлежности элемента к определенному подмножеству.

Дадим основные определения.

• Величина sup _A(x) называется высотой нечеткого множества A. Нечеткое множество A нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 1. При sup _A(x)<1 нечеткое множество называется субнормальным.

• Нечеткое множество называется пустым, если его функция принадлежности равна нулю на всем множестве Х, т.е. ₀(x)=0  xX.

Нечеткое множество пусто, если  xE  _A(x)=0. Непустое субнормальное множество можно нормализовать по формуле

(рис. 1).

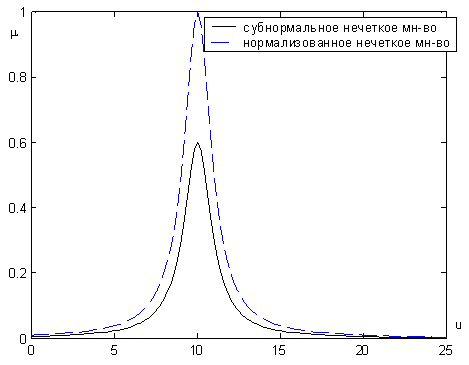
Рис.1. Нормализация нечеткого множества с функцией принадлежности. .

Носителем нечеткого множества А (обозначение supp A) с функцией принадлежности _A(x) называется множество вида suppA={x|xX, _A(x)>0}. Для практических приложений носители нечетких множеств всегда ограничены. Так, носителем нечеткого множества допустимых режимов для системы может служить четкое подмножество (интервал), для которого степень допустимости не равна нулю (рис.2).

Рис.2. Понятие носителя нечеткого множества (выделен жирной чертой)

• Точкой перехода А называется элемент х множества Х, для которого _A(x)=0,5.

• Ядром нечеткого множества называется четкое подмножество универсального множестваU, элементы которого имеют степени принадлежности, равные единице, . Ядро субнормального нечеткого множества пусто.

• α-сечением (или множеством α-уровня) нечеткого множества называется четкое подмножество универсального множестваU, элементы которого имеют степени принадлежности, большие или равные α: .

Рис. 3. Ядро, носитель и α-сечение нечеткого множества

Значение α называют α-уровнем. Носитель (ядро) можно рассматривать как сечение нечеткого множества на нулевом (единичном) α-уровне.

Рис. 3 иллюстрирует определения носителя, ядра, α-сечения и α-уровня нечеткого множества.

Операции над нечеткими множествами

Определения нечетких теоретико-множественных операций объединения, пересечения и дополнения являются обобщениями из обычной теории множеств. В отличие от обычных множеств в теории нечетких множеств степень принадлежности не ограничена лишь бинарной значениями 0 и 1 – она может принимать значения из интервала [0, 1]. Поэтому нечеткие теоретико-множественные операции могут быть определены по-разному. Ясно, что выполнение нечетких операций объединения, пересечения и дополнения над нечеткими множествами должно дать такие же результаты, как и при использовании обычных канторовских теоретико-множественных операций. Ниже приведены определения нечетких теоретико-множественных операций, предложенные Л. Заде.

1. нечеткие множества А и В равны, если _A(x)=_В(x);

2. нечеткое множество С является подмножеством В, т.е. С В, если _С(x) _В(x);

3. нечеткие множества можно объединять – АВ, тогда _AВ(x)= max {_A(x), _В(x)};

4. нечеткие множества могут пересекаться АВ, тогда _AВ(x)= min {_A(x), _В(x)};

5) прямое произведение нечетких множеств АхВ: _АxB(x)= _А(x) _B(x);

6) алгебраическая сумма A+B: _А+В(x)=_А(x)+_В(x)-_АВ(x);

7) дополнением нечеткого множества А называется нечеткое множество с функцией принадлежности .

На рис. 4 приведен пример выполнения операции нечеткого дополнения.

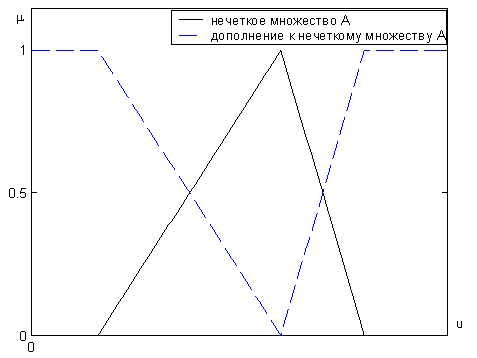
Рис. 4. Дополнение нечеткого множества

Пример 1. Рассмотрим нечеткие множества

suppA = { x| величина x близка к 1},

suppB = {x| величина x очень близка к 1}.

Ясно, что ВА, т.е. функции принадлежности этих множеств _A и _В должны удовлетворять неравенству _В(x)_А(x) при любом xX. Графики этих функций могут выглядеть, например, как показано на рис. 5.



1

_A

_B

0 1 x

Рис. 5. Функции принадлежности