NEWsbornik

ЛИТЕРАТУРА (продолжение)

17.Яхъяева Г.Э. Неч¼ткие множества и нейронные сети. М.: Интернет-Университет Информационных Технологий; БИНОМ. Лаборатория знаний, 2008.

18.Лорьер Ж.-Л. Системы искусственного интеллекта. М.: Мир, 1991.

19.Рейуорд-Смит В.Дж. Теория формальных языков. М.: Радио и связь, 1988.

20.Гулина О.М. Введение в теорию формальных языков. Учебное пособие по курсу "Языки и грамматики. Обнинск: ИАТЭ, 2000.

21.Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. М.: Наука, 1983.

22.Насыров З.Х. Конспект лекций и задачи по курсу "Дискретная математика". Обнинск: ИАТЭ, 1989.

23.Насыров З.Х. Логика, комбинаторика, графы. Учебное пособие по курсу "Дискретная математика". Обнинск: ИАТЭ, 1990.

24.Насыров З.Х. Элементы теории множеств и общей алгебры. Учебное пособие по курсу "Дискретная математика". Обнинск: ИАТЭ, 1990.

25.Насыров З.Х. Множества, отношения, алгоритмы. Учебное пособие по курсу "Дискретная математика". Обнинск: ИАТЭ, 1997.

26.Насыров З.Х. Дискретная математика. Учебное пособие. Обнинск: ИАТЭ, 1999.

27.Насыров З.Х. Логика, комбинаторика, графы. Учебное пособие по курсу "Дискретная математика". 2-е изд. перераб. Обнинск: ИАТЭ, 2001.

28.Насыров А.З., Насыров З.Х. Алгоритмы и их сложность. Учебное пособие по специальности "Прикладная математика". Обнинск: ИАТЭ, 2002.

29.Насыров А.З., Насыров З.Х. Дискретная математика. Учебное пособие. Обнинск: ИАТЭ, 2003.

74

ПРЕДИСЛОВИЕ

Настоящий "Сборник задач"предлагается студентам, изучающим дисциплины "Дискретная математика"и "Математическая логика и теория алгоритмов"в объеме, предусмотренном госстандартом по направлениям "Вычислительная техника и информатика", "Прикладная математика и информатика"и соответствующим специальностям.

Теоретический и справочный материал в этом пособии отсутствует, включение его потребовало бы увеличения запланированного объема в 2 4 раза. Необходимые теоретические сведения можно найти в литературе, список которой помещен в конце данного "Сборника задач".

Задачи в этом сборнике подобраны с таким расчетом, чтобы часть их можно было использовать для аудиторной работы под руководством преподавателя, а оставшаяся часть рекомендуется автором для самостоятельного решения эти задачи помечены кружочком. К задачам имеются ответы и указания. Кроме того, в данном сборнике имеется раздел, в котором приводятся контрольные задания для рубежного и итогового контроля; каждая задача из этого раздела предлагается в 30 вариантах.

Сборник отражает многолетний опыт преподавания дисциплин "Дискретная математика"и "Математическая логика и теория алгоритмов"в ИАТЭ на кафедре прикладной математики. За эти годы содержание курса "Дискретная математика"постепенно менялось, во-первых, из-за изменения учебных планов, во-вторых, в результате обсуждения программы этого курса с коллегами по работе, им авторы выражают благодарность за полезные советы и замечания по поводу содержания данного сборника.

3

+j1(y)(z + 2) + j2(y)z) + j2(x)(j0(y)(z + 2) + j1(y)z + j2(y)(z + 1)) = = x + y + z.

72

à)15. Найдите значения x, y, z , åñëè

x yz = 1; á) x y xz = 0.

16.Выразите через и q .

17.Выразите через и q .

18.o Докажите, что q не выражается через è .

Импликация, эквиваленция и сумма по модулю 2

19. С помощью правила исключения импликации докажите, что

q20 → q30R, q30 → q00L(q0q0HL), q31 → q40L,

q40 → q51R(q5q1Z ◦ HL). 426. Например: q10 → q20E(q2q3T ),

q30 → q40R, q41 → q00L(q0q0HL ◦ Z ◦ HL), q40 → q50L, q50 → q61R(q6q1HL2), ãäå

T = HRа) например,◦ F A ◦ T R ◦ HR ◦ T R ◦ C ◦ T R ◦ EQ ◦ HL ◦ T R ◦ HR.

427. A = B = N ; б) например, A = {n Z|n 6 4}, B = N . 429. а) например, A = Z B = N ; б) например,

A = {n Z|n > −4}, B = N . 430. Указание. Используйте, что Q счетно. 431. Указание. См. задачу 430.

432. JA = sg(x −. [x]2). 433. JA = sg(|x − y + 1|).

x

Q

434. JA(x) = sg |x − f(i)|. 436. π(3; 4) = 31, l(33) = 5,

i=0

r(33) = 2. 437. 62. 438. x = 0, y = 1, z = 3. 442. Пусть

рекурсивные= {(x(k), y(kфункции)) | k N. Тогда}, ãäå x(k), y(k) примитивно

0

f(t) = y(µk(x(k) = t)).

443.правилаL = a{b} b{a} . 444. L = {a2b}+c . 445. G имеет имеет правилаI → ε перехода| aA, A → aB , B → bC , C → cD, D → c | cI ; K

I → aA | cB , A → b | bI , B → c | cI ; K имеет правила перехода

перехода I → b | aA | bI1 , A → bI , I1 → b | bI1 ; K имеет правила правила q1a → q2 , q1b → q3c , q2b → q1 , q3b → q3c . 451. G имеет

I → a | b | aA | bA,

A → a | b | 0 | 1 | 2 | aA | bA | 0A | 1A | 2A. 452. G имеет правила

I → a | b | aA | bA, A → a | b | 0 | 1 | 2 | aB | bB | 0B | 1B | 2B , B → a | b | 0 | 1 | 2. 453. I → b | aI | bI . 454. I → aA | bB , A → a | aI | bC , B → b | bI | aC , C → aB | bA. 455. G имеет

70

i1, i2, . . . , ik , в которых стоят 1.

Реализация булевых функций в ДНФ и КНФ.

Релейно-контактные схемы

В задачах 52 57 требуется найти минимальную ДНФ и построитьзаданнойконтактнуютаблично. схему по этой ДНФ для булевой функции f ,

59.Докажите, что правило склеивания является следствием правил поглощения и образования союзов.

Âзадачах 60 65 требуется найти минимальную ДНФ и построить контактную схему по этой ДНФ для булевой функции, заданной с помощью формулы.

60.x y x zt y zt.

61.x y z t x y z y z t xy z t x zt.

62.(x yz)( x → y) ( xyz x).

((x y) z) ( x y) z .

7

397. Например, q10 → q20R, q21 → q21R, q20 → q31L, q31 → q31L, q30 → q40R, q41 → q00L. 398. Например,

q10 → q20R, q21 → q21R, q20 → q31R, q31 → q31R, q30 → q40L,

q30 → q40R, q40 → q50R, q50 → q00E , q51 → q51E , q31 → q60R, q60 → q71R, q70 → q70E , q71 → q81R, q81 → q81R, q80 → q90L,

q30 → q30E , q31 → q40L, q40 → q40E , q41 → q50L, q51 → q51L,

q50 → q00E . 405. Например, q10 → q20R, q20 → q01L,

q31 → q41R, q41 → q41R, q40 → q50L, q51 → q60L, q61 → q61L,

q31 → q40R, q41 → q41R, q40 → q50L, q51 → q60L, q61 → q70L, q71 → q71L, q70 → q20E , q60 → q81L, q81 → q81L, q80 → q00E , q30 → q90R, q91 → q91R, q90 → q100L, q101 → q100L,

q30 → q40L, q41 → q50L, q51 → q51L, q50 → q21R, q40 → q20E ,

q20 → q60L, q61 → q61L, q60 → q00E . Указание.

f(x) =Например,1 + f(x − 2). 410. Аналогично программе для [x/2].

411. q10 → q20R, q20 → q00L, q21 → q31R,

q30 → q40L, q41 → q00L, q31 → q50R, q51 → q50R, q50 → q60L,

q60 → q60L, q61 → q01L. 412. Например, q10 → q20R,

q20 → q00L, q21 → q31R, q30 → q40L, q41 → q01L, q31 → q50R, q50 → q60L, q60 → q40L, q51 → q70R, q71 → q70R, q70 → q80L,

68

71. f(x, y, z) = (1111 0010)T .

72. g(a, b, c, d) = (0000 0001 1101 0001)T .

73.o f(a, b, c, d) = (1100 1010 0011 0010)T .

В задачах 74 76 требуется найти минимальную КНФ для булевой функции, заданной с помощью формулы.

74. (a b (b → c)) → a c.

75. (c → b) → (a bc ac).

76.o ((d → bc) → (a(b c) bc)) a bc.

Функциональные схемы.

Полнота систем булевых функций

В задачах 77 79 требуется из элементов И-НЕ построить функциональную схему, реализующую указанную булеву функцию.

77. f(x, y, z) = xy xz yz .

78. g(a, b, c, d) = (0 − 4, 7, 11, 12, 15).

79.o f(a, b, c) = (a c) → b(a → c).

80. Стрелкой Пирса называется функция x ↓ y = (1000)T . Äî- кажите, что {x ↓ y} базис, выразите в нем , , q .

o

â81ýòîé. Докажите,системе что система {x → y, 0} образует базис, выразите

, ,

В задачах 82 85 требуетсяq . проверить полноту данной систе-

мы булевых функций и указать базис.

86.Докажите, что q нельзя выразить через {, , →, }.

87.Докажите, что → нельзя выразить через {, , }.

88.o Докажите, что → нельзя выразить через {q, }. 9

317.

одновременно319. Указаниевершину.Простойстепениграфа с0 nи вершинувершинамистепенине может иметь

обозначатьm 6 2 èëè nребром6 2. 330красного. n 6 4цвета,.333à. Указаниенезнакомство.Если синимзнакомство

цветом, то из любой вершины выходят по крайней мере три

ребра одного цвета. 334. Расположим вершины x , x , . . . x окружности в вершинах правильного 21-угольника1. Рассмотрим2 21 íà

344.граф имеетmболееиn двухчетнынечетных.346.вершинНельзя,. т.к. соответствующийИмеется3 дерева

358. x(x − 1)(x − 2)3 . 359. Ñòåê S и очередь T меняются так:

S : 1, 6, 7, 2, −2, 3, 4, −4, −3, 5, 8, 9, 10, −10, −9, −8, −5, −7, −6, −1;

T : 1,Øàã6, −1возврата, 7, −6, 2, 3происходит, 4, 5, −7, −2против, −3, −4стрелки, 8, −5, 9.,Ñòåê10, −8, −9, −10.

360.

105. P (x, y) = (x2 + y2 6 1) (xy > 0).

106.o P (x, y) = (|x| > |y|) (|x| > 1).

тинностиВзависимостиследующихот предикатовзначенияпараметра(107 111)a .найдите области ис-

107. P (x) = (x + a < 1) → (1 + a > 2x), åñëè x [0; 1], a R.

108. P (x) = (|3x − a| + |2x + a| 6 5), åñëè x R, a R.

109.o P (x) = (a < x + 1), åñëè x [0; 1], a [0; 3].

110.o P (x) = (x2 + a2 6 1) (x 6 0), åñëè x R, a R. 111.o P (x) = (x2 + 2|x + a| + 32 a < 0), åñëè x R, a R.

Кванторы и их свойства

112. Вычислите значения предикатов

Aà) = x(x > 2 x < 5) è B = x(x > 2 x < 5), åñëè x [3; 4], á) x [0; 2], â) x N.

à)113.o Сравните значения высказываний A è B , åñëè

á) A = x(x > 2 x < 3), B = x(x > 2) x(x < 3), x R;

A = x(x > 2 → x < 5), B = x(x > 2) → x(x < 5), x [3, 6].

В задачах 115 118 требуется найти множество всех значений y, для которых является истинным указанный предикат P (y).

115. x(xy < 1 → x > −1), åñëè x, y R.

116. x(y > x2) (y 6 1), åñëè x R, y [−2; 2].

117. (y > 5) x(y > x2), åñëè x [−2; 2], y R.

118.o y > 0 x(x2 + y2 6 2 y > x), åñëè x, y R.

сравните119. Докажите,значениячтовысказыванийx P (x) x Q(x) = x(P (x) Q(x));

A = x(x < 2 x > 3) è B = x(x < 2) x(x > 3), åñëè x R.

B = , 3) A = B . 170. DR = {1; 2; 3}, VR = {2; 3; 4},

R = {(1; 1), (2; 1), (2; 2), (3; 1), (3; 2), (3; 3), (4; 1), (4; 2), (4; 3), (4; 4)} R−1 =à){(2; 1), (3; 1), (3; 2), (4; 1), (4; 2), (4; 3)}.

171. DR = {1; 2; 3; 4}, VR = {12; 16}, R = {(3; 16), (5; 12), (5; 16)},

R−1 = {(12; 1), (12; 2), (12; 3), (12; 4), (16; 1), (16; 2), (16; 4)}.

172. DR = [0; 2], VR = [−1; 1],

R = {(x, y) | x [0; 3], y [−1; 2], x2 + 4y2 > 4}, R−1 = {(x, y) | x [−1; 2], y [0; 3], 4x2 + y2 6 4}.

173. DR = P (M), VR = P (M), R = {({x}, ), ({y}, ), (M, ), (M, {x}), (M, {y}), ({x}, {y}), ({y}, {x})},

R−1 = {({x}, ), ({y}, ),

á)R =например,{(a, a)}. 189. а) Например, R = {(a, a), (b, b), (c, c), (a, b)},

R= {(a, a), (b, b), (a, b), (b, a)}.

190.Rt = {(x, y) | y > x + 1}, Rc = {(x, y) | y = x ± 1},

Rr = {(x, y) | x 6 y 6 x + 1}. 191. Например,

R1 = à){(1, 2), (2, 1)}, R2 = {(1, 3), (3, 1)}.

201. Ka = {a, b}, Kc = {c}, á) K0 = {3k},

K1 = {3k + 1},K2 = {3k + 2}, ãäå k Z, â) Kx = x + Z, x [0; 1). 202. R =

{(a, a), (b, b), (c, c), (d, d), (b, c), (c, b), (b, d), (d, b), (c, d), (d, c)}.

M= {a, b, c, d}, R = {(a, c), (a, d)} IM , A = M ; б) например,

M= {a, b, c}, R = {(a, c), (b, c)} IM , A = {a, b}; в) например,

A = M = {x} (0; 1), считая, что x несравним с любым y (0;Например,1); г) например, M = (−∞; ∞), A = (0; 1).

(m + n) < (m0 + n0) ((m + n) = (m0 + n0) m 6 m0).

64

,

,

В задачах 131 135 найдите предваренную и сколемовскую форму указанного предиката.

131. x y P (x, y) → x Q(x).

132. x y P (x, y) x Q(x).

133. x P (x) x Q(x).

134. P (x) x Q(x).

135.o x P (x) x Q(x).

136. Запишите в предваренной форме следующие утверждения: б)а) f(x) непрерывна на множестве M ,

â) f(x) равномерно непрерывна на множестве M ,

f(x) не является равномерно непрерывной на множестве M .

2. Теория множеств

Объединение, пересечение и разность множеств

предикаты:137. Выразите через p = (x A) è q = (x B) следующие

полна,x y =базисом(x → 0) является→ y, xy =система,(x → (yсостоящая→ 0)) → 0èç.82второй. Системафункции.

83. Система является базисом. 84. Система полна, базисом является система, состоящая из второй и третьей функции.

85.системыСистемасохраняютполна при1. n >Указание2. 86. Указание.Функции.Функцииданной системыданной

87.

сохраняют 0. 88. Указание. Функции данной системы линейны. 89. а) Например, f(x) = x, á) g(x) = 1, в) например,

hфункции(x, y) = x y. 90. Указание. Найдите все самодвойственные

полноту{ x, x y}, в) используйте полноту {xy, x y, 1}, г) используйте

{x y x z y z, 1}. 96. [2; 3). 97. x (−∞; 2) {3}.

98.x (−∞; 1] [2; ∞). 99. x (−∞; 2] [4; 5).

Ðèñ. 16 Ðèñ. 17

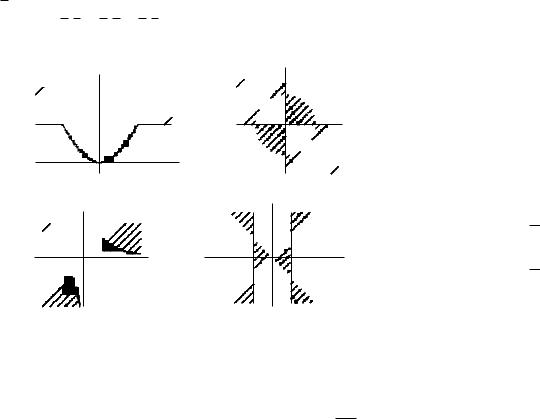
102. СмЧетвертая.рис. 16четверть.Смплоскости.рис. 15; отмеченные(x, y). 103.областиСм.рис.внутри14.

104. 105.

круга содержат граничные точки, а области вне круга не содержат граничных точек. 106. Ñì. ðèñ. 17. 107. Åñëè

a (−∞; −1], òî x ; åñëè a (−1; 0), òî x [0; a+12 ); åñëè 62

â)á)o A × (B ∩ C) = (A × B) ∩ (A × C), ã)o A × (B \ C) = (A × B) \ (A × C), o A × (B4C) = (A × B)4(A × C).

164. Докажите, что A × B = (A × D) ∩ (C × B), åñëè A C è

B D.

Докажите следующие утверждения (165 168).

165. (A ∩ B) × (C ∩ D) = (A × C) ∩ (B × D).

166.o (A × B) (C × D) (A C) × (B D).

167. (C × D) \ (A × B) = ((C \ A) × D) (C × (D \ B)).

168.o (A×B)4(C ×D) ((A4C) ×(B D)) ((A C) ×(B4D)).

172. R = {(x, y) | x [0; 3], y [−1; 2], x2 + 4y2 6 4}.

173.o R = {(a, b) | a, b P (M), a b}, ãäå M = {x, y}.

174. Пусть R = {(x, y) | y > x2}, ãäå x, y R. Найдите R(M),

R(M), R−1(M), åñëè M = [−1; 2].

175.o Пусть R = {(x, y) | x > 2y}, ãäå x, y R. Найдите R(M),

R(M), R−1(M), åñëè M = [−2; 6].

В задачах 176 179 найдите композицию R1 ◦ R2 .

176. R1 = {(a, x), (a, y), (b, y)} {a, b} × {x, y, z}, R2 = {(x, p), (x, q), (z, q)} {x, y, z} × {p, q}.

177. R1 = {(x, y) | y > x2} R × R, R2 = {(y, z) | z > 2y} R × R.

R1 = {(x, y) | y > x2} R × R, R2 = {(y, z) | z 6 2y, } R × R.

15

60

197.Åñëè R транзитивно, то R ◦ R тоже транзитивно.

198.Åñëè R транзитивно, то R ◦ R R.

Åñëè R1 R2 транзитивно, то R1 ◦ R2 R1 R2 .

200.o Åñëè R рефлексивно и транзитивно на M , òî R = R ◦ R. шениями201. Докажите,эквивалентности,что следующиенайдитеотношенияразбиение указанногоR являютсямножеотно--

ства на классы эквивалентности:

á)à) R = {(a, a), (b, b), (c, c), (a, b), (b, a)} íà {a, b, c}, â) R = {(x, y) | (x + 2y) . 3} íà Z,

o R = {(x, y) | y − x Z}, x, y R.

разбивает202. Какоенаотношениеподмножестваэквивалентности множество M = {a, b, c, d}

M1 = {a} è M2 = {b, c, d}?

Докажите следующие утверждения (206 209).

206.Åñëè R1, R2, R1 R2 эквивалентности, то R1 R2 = R1◦R2 .

207.Åñëè R1, R2, R1 ◦R2 эквивалентности, то R1 ◦R2 = R2 ◦R1 .

208.o Åñëè R эквивалентность на M , òî R ◦ R−1 = R.

17

18) (a c d)(a b c)( a b d)( a c d) ` a c d a c b d, 19) (a b d)(a b d)( a c d)( a b c) ` a b d a c b d, 20) (a b)( a c d)( a b d) ` a b b d a c d,

21) (a c d)( b c d)( a c d) ` a d a c b c d, 22) (b c d)( b c d)( a b d) ` a b d b c c d,

23) ( b c d)( b c d)( a b c)( a c d) ` a b b c d c d, 24) (a c d)( b c d)( a b c) ` a c a d b c,

25) (b c d)(a b c)( a c d)( a b c) ` a b c b d a c, 26) (c d)( a d)(b c) ` b d a b c c d,

27) (a b d)(b c d)( a c d)( a b d) ` a c d a b b c d, 28) ( a b c)( b c d)(b c d)( a b c) ` b c a d b c, 29) ( a b)(c d)( a c)(b d) ` a d a b c b c d.

Нечеткая и многозначная логика

предикатов528. Пусть A, B, C, D, E множества и даны нечеткие значения

µ(x A) = 0, 2, µ(x B) = 0, 4, µ(x C) = 0, 5,

Найдитеµ(x D)нечеткое= 0, 1, значениеµ(x E)предиката= 0, 6 для некоторого элемента x.

á)à) R = {(a, r), (b, p), (b, q), (c, p), (d, r)}, â) R = {(a, q), (b, p), (d, r)},

R = {(a, q), (b, q), (c, p), (d, p)}?

221. Выясните инъективность, сюръективность и биективность следующих функций:

à) F : [−1; 2] → [0; 5], F (x) = x2 , á) F : [−1; 2] → [0; 4], F (x) = x2 , â) F : [1; 2] → [0; 4], F (x) = x2 ,

ã) F : [−2; −1] → [1; 4], F (x) = x2 .

222.o Выясните инъективность, сюръективность и биективность F : N → N, вычисляемых по формулам

F (n) = n + 2, á) F (n) = [ n+12 ], â) F (n) = (n − 2)2 + 1,

ã) F (n) =

n + 1, åñëè n нечетно, n − 1, åñëè n четно.

o →

à)223сюръективно,. Приведитенопримерне инъективно,отображения f : Z Z, которое

б) инъективно, но не сюръективно. а)224Докажите,. Пусть f÷òî: X → Y , A, B X .

б) Приведите пример,f(A когда∩ B) f(A) ∩ f(B).

в) Докажите, что f(A ∩ B) 6= f(A) ∩ f(B).

г) Докажите, что f(A ∩ B) = f(A) ∩ f(B), åñëè f инъекция. для любых f инъекция, если f(A ∩ B) = f(A) ∩ f(B)

A, B X .

г) Докажите, что если f инъекция, то f(A) \ f(B) = f(A \ B).

à)226. Найдите p = f ◦ g è q = g ◦ f , åñëè

á) f : R → R, f(x) = x2 , g : R → R, g(x) = x + 1;

â) f : N0 → N0 , f(n) = n + 1, g : N0 → N0 , g(n) = |n − 1|,

o f : Z × Z → Z, f(m, n) = m + n, g : Z → Z × Z, g(n) = (n, n).

19