
Karmanov_Trojanov
.pdf
Волновую функцию задаем следующим программным блоком и готовим массивы для графика схемы уровней
ψ(x,e,A,B) := |
for j 1 .. N |
|
|
break if (Xj−1 ≤ x) (x ≤ Xj) |
|
|
y ← Aj exp(i k(e, j) x) + Bj exp(−i k(e, j) x) |
|
|
y ← B0 exp(−i k1(e) x) |
if (x ≤ X0) |
|
y ← AN+1 exp(i k1(e) x) |
if x ≥ XN |
|
y |
|
Пусть |
|
|
|
e0 := eL0 |
e0 = −24.363 |
A0 := AB(e0)0 |
B0 := AB(e0)1 |
e1 := eL1 |
e1 = −23.369 |
A1 := AB(e1)0 |
B1 := AB(e1)1 |
e2 := eL2 |
e2 = −23.362 |
A2 := AB(e2)0 |
B2 := AB(e2)1 |
Для того, чтобы было удобно сопоставлять между собой значения волновых функций разных состояний, выполним их нормировку:
|
⌠∞ |
Ψ0(x)2 dx |
|
Ψ0(x) |
Ψ0(x) := ψ(x,e0,A0,B0) |
C0 := |
Ψ0(x) := |
||
|
⌡− ∞ |
|
|
C0 |
|
⌠∞ |
Ψ1(x)2 dx |
|
Ψ1(x) |
Ψ1(x) := ψ(x,e1,A1,B1) |
C1 := |
Ψ1(x) := |
||
|
⌡− ∞ |
|
|
C1 |
|
⌠∞ |
Ψ2(x)2 dx |
|
Ψ2(x) |
Ψ2(x) := ψ(x,e2,A2,B2) |
C2 := |
Ψ2(x) := |
||
|
⌡− ∞ |
|
|
C2 |
Ψ0(x) := Ψ0(x) 100 Ψ1(x) := Ψ1(x) 100 Ψ2(x) := Ψ2(x) 100 |
||||
Сформируем массивы для графика схемы уровней. |
|
|
||
m := 0 .. 1 j := 0 .. Nlev − 1 |
|
|
|
|
Elevm, j := eLj |
Xe0, j := 0 |
Xe1, j := XN |
|
|
20
|
60 |
|
|
|
|
|
Ψ0(x) |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
Ψ1(x) |
|
|
|
|
|
|
Ψ2(x) |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
Ugr |
|
|
|
|
|
|
Elev |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
|
|
|
|
x,x,x,Xgr ,Xe |
|
|
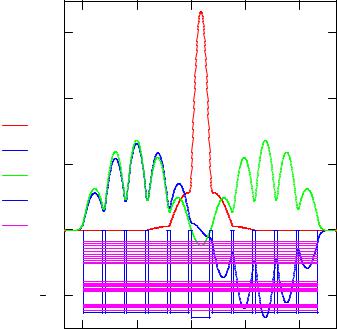
Рис. 6. |
Схема уровней энергии и волновые функции первых |
|||||
|
|
состояний в потенциальной решетке с дефектом |
||||
Как видно из этого рисунка, наличие симметрично расположенного дефекта в потенциальной решетке с выбранными параметрами приводит к появлению основного состояния, лежащего заметно ниже первой группы уровней, отвечающих всем остальным атомам решетки, если принять во внимание взаимное расстояние (по энергии) между этими уровнями. При увеличении энергии состояния во второй и третьей группах этот эффект уже нивелируется и уровень, ассоциированный с дефектным атомом, уже явно не выделяется.
Волновая функция основного состояния системы в данном случае ассоциирована с дефектным атомом и сильно отличается как от волновых функций соседних состояний, так и от волновой функции основного состояния бездефектной решетки, прежде всего, тем, что она в основном локализована в окрестности атома - дефекта.
21
Упражнения
1. Рассчитайте уровни энергии и волновые функции в симметричной потенциальной решетке для различных значений N0 – числа атомов в решетке на основе решения исходной системы уравнений для коэффициентов волновой функции (см. пункт 1 этой главы). Как изменяются границы областей энергии, в которых расположены группы уровней при увеличении количества атомов в решетке?
2. Матричным методом рассчитайте уровни энергии и волновые функции в симметричной потенциальной решетке для различных значений N0 – числа атомов в решетке. Сопоставьте свои результаты с результатами расчета в упр. 1.
3.Рассчитайте уровни энергии и волновые функции в симметрич-
ной потенциальной решетке для N0 = 10 атомов. Проверьте условия ортогональности волновых функций. Постройте график волновой функции и плотности вероятности для нижних состояний в каждой группе по энергии, т.е. при l = 0, 10, 20. Как ведет себя огибающая волновой функции? Как изменяется поведение огибающей при l = 1,11,21? Вычислите, как зависит сумма плотностей вероятности по состояниям одной группы от координаты x, отсчитываемой вдоль решетки. Постройте график этой функции.
4.Рассчитайте уровни энергии и волновые функции в несиммет-
ричной потенциальной решетке с дефектомдля N0 = 11 атомов в решетке на основе решения исходной системы уравнений (см. п. 1 этой главы) и сопоставьте Ваши результаты с обсуждавшимися выше. Какой из этих методов является более трудоемким?
5.Постройте схему уровней энергии, волновые функции и плотности вероятности для состояний одной группы по энергии в решетке с дефектом. Вычислите, как зависит сумма плотностей вероятности по состояниям одной группы от координаты, отсчитываемой вдоль решетки. Сравните Ваши результаты с аналогичными результатами для бездефектной решетки.
6.Проанализируйте изменения в форме волновой функции основного состояния системы при условии, что размер и глубина потенциальной ямы дефекта приближается к стандартным для выбранной решетки. Как изменяется при этом сумма плотностей вероятности по состояниям одной группы от координаты, отсчитываемой вдоль решетки?
22
7.Вычислите волновые функции нескольких состояний из второй группы уровней. Попытайтесь определить, какое из состояний, лежащих во второй группе, может быть ассоциировано с дефектным атомом при выбранных параметрах системы.
8.На основе вычислительного эксперимента найдите, при каких параметрах ямы дефектного атома ассоциированный с ним уровень энергии расположен выше уровней первой группы. Можно ли добиться появления такого уровня выше верхней группы уровней? Это могло бы изменить свойства проводимости модельной системы.
9.Найдите условия, при которых ассоциированный с дефектным атомом уровень энергии "поглощается" первой группой уровней.
10.Как зависит положение уровня энергии атома-примеси в спектре от расположения его потенциальной ямы в решетке?
11.Как зависит форма волновой функции состояния системы, ассоциированной с атомом-примесью, от расположения его потенциальной ямы в решетке?
12.Предположим, что потенциальная решетка содержит дефект – вакансию. Рассчитайте уровни энергии и волновые функции нескольких состояний. Постройте схему уровней энергии, волновые функции
иплотности вероятности для этих состояний. Вычислите, как зависит сумма плотностей вероятности по состояниям одной группы от координаты x, отсчитываемой вдоль решетки. Сравните Ваши результаты с аналогичными результатами для бездефектной решетки.
13.Будем считать, что одномерная модель аморфного твердого тела представляет собой цепочку одинаковых потенциальных ям, разделенных барьерами переменной ширины. Задавая ширину барьеров согласно какому-либо правилу (или распределению случайных величин со средним значением, близким к ширине барьера однородной цепочки атомов), вычислите спектр энергий и сопоставьте его со спектром однородной цепочки атомов. Сохраняется ли и в этом случае "зонная" структура спектра?
14.В условиях упражнения 13 рассчитайте волновые функции и плотности вероятности для нескольких состояний и постройте их графики. Как изменяется сумма плотностей вероятности по состояниям одной группы от координаты x, отсчитываемой вдоль решетки?
Постройте график волновой функции и плотности вероятности для нижних состояний в каждой группе по энергии, т.е. при l = 0, 10, 20.
23
Глава 2. Зонная структура кристалла в модели Кронига-Пенни
(решение нелинейных уравнений)
Одной из важнейших особенностей движения электрона в периодическом поле является зонная структура энергетического спектра. В простейшем случае, когда потенциальная энергия V(r) является постоянной величиной, решение уравнения Шредингера, функция Блоха [7], переходит в обычную плоскую волну, а энергия электрона E(k) оказывается связанной с импульсом hk обычным соотношением, характерным для свободного движения частицы,
E(k) = (h k)2 . 2 m
В общем случае движения частицы в периодическом поле энергия уже не является всюду непрерывной функцией импульса. Вместо этого E(k) распадается на ряд зон, в пределах каждой из которых энергия изменяется непрерывно и испытывает разрывы на границах этих зон. Весь энергетический спектр разбивается при этом на ряд зон разрешенных значений энергии, которые отделены друг от друга энергетическими щелями – областями запрещенных значений энергии.
Основное уравнение
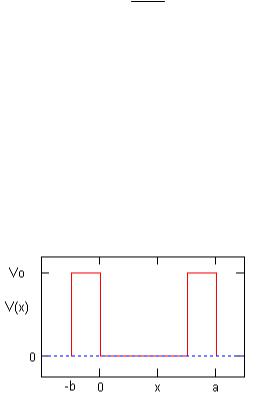
Одним из простейших примеров периодического поля, допускающих точное решение, является задача Кронига - Пенни. Рассмотрим движение электрона в одномерном периодическом поле, показанном на рис. 1.
Рис. 1. Потенциал в модели Кронига-Пенни
24
Уравнение Шредингера в данном потенциальном поле имеет вид
|
∂2 |
|
ψ(x) + |
2m |
(E −V (x))ψ(x) = 0 , |
|||||
|
∂x2 |
|
h2 |
|||||||
|
|
|
|
|
|
|
|
|||
где V(x) = V |
|
в области барьера и нулю - в пределах ямы. |
||||||||
0 |
|
|
2mE |
|
|
|
2m(V0 − E) |
|
||
Обозначим |
α2 = |
|
, |
β 2 = |
, |
|||||
|
|
|
|
h2 |
|
|
h2 |
|||
с учетом того, что |
|
0 ≤ E ≤ V |
|
и будем искать решение в виде |
||||||
|
|
0 |
|
|
|
|
||||
ψ1 (x) = A exp(iα x) + B exp(−iα x)
ψ2 (x) = C exp(β x) + D exp(−β x)
вобласти ямы и барьера, соответственно.
Условия непрерывности волновой функции и ее производной на границах в точках -b, 0, a-b с учетом равенства
ψ (x + a) = exp(ika)ψ(x) ,
выражающего свойство трансляции волновой функции в периодическом потенциале, приводят к следующей системе линейных алгебраических уравнений для коэффициентов волновых функций A,B,C,D:
C + D = A + B , |
|
C − D = i α ( A − B ) , |
|
|
β |
C e − β b |
+ D e β b = e −ik a ( A e |
C e − β b |
− D e β b = e −ik a ( A e |
iα ( a −b )
iα ( a −b )
+B e
−B e
−iα ( a −b )
−iα ( a −b )
) ,
) i αβ .
Из первых двух уравнений находим
C = |
1 |
((A + B) +i |
α |
(A − B)) |
, |
|
2 |
β |
|||||
D = |
1 |
((A + B) −i |
α |
(A − B)) , |
||
2 |
β |
|||||
|
|
|
|
|||
25
а правую часть третьего и четвертого уравнений представим в форме:
Aeiα(a−b) + Be−iα(a−b) =(A+B)cosα(a −b) +i(A−B)sinα(a −b),
Aeiα(a−b) −Be−iα(a−b) =(A−B)cosα(a −b) +i(A+B)sinα(a −b).
Подставляя выражения для C и D в левую часть третьего и четвертого уравнений и группируя слагаемые относительно A+B и A - B, получаем систему из двух уравнений для определения суммы и разности коэффициентов A и B.
( A + B)
( A + B)
[chβb − e−ika cos α(a − b)]=
i( A − B) α shβb + e−ika sin α
β
|
α |
|
= |
shβb − |
β |
e−ika sin α(a −b) |
|
|
|
|
i αβ ( A − B)[chβb − e−ika cos α
(a
(a
− b)
− b)]
Поскольку эта система уравнений однородна, то ее нетривиальное решение существует, если только определитель матрицы системы обращается в ноль. Этот факт дает возможность выписать основное уравнение для определения допустимых значений параметра α или энергии E:
β 2 −α2 |
shβb sinα(a −b) +chβb cosα(a −b) = cos ka . |
|
2αβ |
||
|
В силу того, что величина k действительна, это уравнение выполняется, если его левая часть принимает значения в интервале [–1, +1]. Поэтому можно найти границы области допустимых значений энергии на основе графического решения этого уравнения. Для графического отделения корней воспользуемся вспомогательной функцией
g (E ) = sign (| f (E) | −1) .
26
|
|
|
Поиск и отделение корней |
||||
Пусть |
a := |
5 A |
b := 1 A |
Vo := 15 eV |
|||
|
mc2 := |
0.511 106 eV |
hc := 1.9732858 103 eV A |
||||
|
α(E) := |
|
2mc2 E |
|
β(E) := |
2mc2 (Vo − E) |
|
|
|
hc |
hc |
||||
|
|
|
|
||||
|
f1(E) := β(E)2 − α(E)2 |
sinh(β(E) b) sin α(E) (a − b) |
|||
|
2 α(E) β(E) |
|
|
|
|
|
f2(E) := cosh(β(E) b) cos α(E) (a − b) |
||||
|
|
f(E) := f1(E) + f2(E) |
|
||
|
g(E) := sign( |
f(E) |
− 1) |
E := |
0.01,0.015 .. Vo |
|
4 |
|
|
|
|
|
2 |
|
|
|
|
f(E) |
|
|
|
|
|
g(E) |
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 0 |
5 |
|
10 |
15 |
|
|
|
|
E |
|
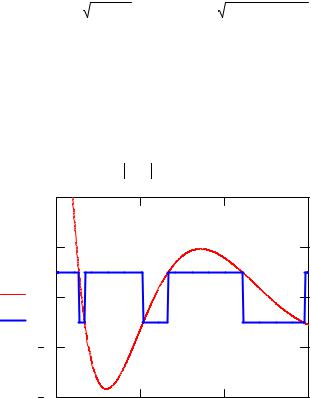
Рис. 2. К определению границ зон допустимых значений энергии |
|||||
Графики обеих функций показаны на рис. 2. Границы зон соответствуют интервалам энергии, в пределах которых функция g(E) = –1. Как видно из рисунка, в данном случае формируются полностью только три зоны допустимых значений энергии.
27
Поиск и отделение корней можно выполнить с помощью следующей подпрограммы, основанной на использовании встроенной функции root(). Для четных или нечетных значений параметра s подпрограмма находит корни уравнений f(E) = ±1.
E_interval(En,Em,de,s) := n ← 0 E ← En
f1 ← f(E) − (−1)s while E < Em
E ← E + de
f2 ← f(E) − (−1)s if (f1 f2 < 0)
E ← E − 0.5 de
Aen ← root f(E) − (−1)s ,E n ← n + 1
f1 ← f2
Ae
Границы интервалов энергии, в которых f(E) = 1:
Ea1 := E_interval(0.01,Vo,0.01,0)
Nlev1 :=  rows(Ea1)
rows(Ea1)
Ea1T = ( 1.313 6.598 11.09 )
Границы интервалов энергии, в которых f(E) = –1:
Ea_1 := E_interval(0.01,Vo,0.01,1)
Nlev_1 := rows(Ea_1) Nlev_1 = 3
Ea_1T = ( 1.655 5.119 14.767 )
28
Расчет дисперсионной кривой
Используя уравнение f(E) = cos(ka) для всех допустимых значений энергии, можно вычислить допустимые (действительные) значения квазиимпульса hk и получить дисперсионное соотношение E(k) для одномерного твердого тела с постоянной решетки, равной a.
Соответствующий расчет можно выполнить, например, с помощью следующей подпрограммы.
Quasi_im(Eg,N,ss,M) := |
for n 0 .. N − |
1 |
|
|
|||||
|
|
as ← (−1)n |
|
|
|
||||
|
|
|
|
|
|||||
|
|
for m 0 .. M |
|
||||||
|
|
|
nm ← m + n (M + 1) |
||||||
|
|
|
|||||||
|
|
|
de ← (Egn,1 − Egn,0) M− 1 |
||||||
|
|
|
e ← Egn,0 + de (m + 0.5) |
||||||
|
|
|
znm,0 ← e |
|
|||||
|
|
|
ka ← acos(f(e)) |
|
|||||
|
|
|
p ← ka |
|
|
|
|||
|
|
|
p ← π − p if as < 0 |
||||||
|
|
|
p ← p + n π |
|
|||||
|
|
|
eka ← |
|
hc2 |
|
p2 |
||
2 mc2 a2 |
|||||||||
|
|
|
|
|
|
||||
|
|
|
if ss > 0 |
|
|
|
|||
|
|
|
|
ka ← π − ka |
if as < 0 |
||||
|
|
|
|
||||||
|
|
|
|
ka ← ka + n π |
|||||
|
|
|
ka ← 0 |
if nm = 0 |
|||||
|
|
|
znm,1 ← ka |
|
|||||
|
|
|
znm,2 ← eka |
|
|||||
|
z |
|
|
|
|||||
29
