
matan_vse_k_ekzamenu_za_1_semestr
.docx
Понятие
подпоследовательности (определение,
свойство, примеры).
Определение:
Пусть
 некоторая числовая последовательность.
Выберем из этой последовательности
бесконечное множество чисел
некоторая числовая последовательность.
Выберем из этой последовательности
бесконечное множество чисел
 ,
, ,
, …,
…, ,…
где
,…
где
 Выбранное
множество {
Выбранное
множество { называется подпоследвательностью
последовательности
называется подпоследвательностью
последовательности
 .
Пример:
.
Пример:
 =1,1/2,1/3,…1/n;
{
=1,1/2,1/3,…1/n;
{ 1/2,1/4,1/6,…1/2n
1/2,1/4,1/6,…1/2n
 подпоследовательность исходной
последовательности Свойство:
каждая подпоследовательность сходящейся
к a
последовательности
подпоследовательность исходной
последовательности Свойство:
каждая подпоследовательность сходящейся
к a
последовательности
 сходится к этому же числу a.
|
сходится к этому же числу a.
| -a|<
-a|<
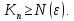
Предельные
точки последовательности (1, 2
определение)Определение
1:
Точка x
числовой
оси называется предельной точкой
последовательности
 ,
если в любой окрестности
,
если в любой окрестности
 й
точки содержится бесконечно много
элементов этой последовательности
й
точки содержится бесконечно много
элементов этой последовательности
 .
Определение
2:
Точка x
числовой
оси называется предельной точкой
последовательности
.
Определение
2:
Точка x
числовой
оси называется предельной точкой
последовательности
 ,
если из этой последовательности можно
выбрать последовательность, которая
сходится к x
,
если из этой последовательности можно
выбрать последовательность, которая
сходится к x
Лемма
4:
Пусть точка x
–
предельная точка последовательности
 .
Тогда из этой последовательности можно
выбрать подпоследовательность, сходящуюся
к числу x.
Доказательства:
Выберем следующее множество значений
.
Тогда из этой последовательности можно
выбрать подпоследовательность, сходящуюся
к числу x.
Доказательства:
Выберем следующее множество значений
 :
:
 ,
,
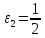 ,…,
,…,
 .
Так как по условию леммы x
– предельная точка последовательности
.
Так как по условию леммы x
– предельная точка последовательности
 ,
то в пределах любой
,
то в пределах любой
 -окрестности
содержится бесконечно много элементов
-окрестности
содержится бесконечно много элементов
 .
Выберем в пределах окрестности x
с
.
Выберем в пределах окрестности x
с
 не который элемент
не который элемент
 исходной последовательности. В
-окрестности с
исходной последовательности. В
-окрестности с выберем
выберем
 (
( ,
и т.д. В -окрестности с
,
и т.д. В -окрестности с выберем
выберем
 .
Набор этих элементов будет составлять
некоторую подпоследовательность {
.
Набор этих элементов будет составлять
некоторую подпоследовательность {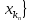 .
.
 .
Поскольку
.
Поскольку

 ,
то x
является предельной последовательностью
{
,
то x
является предельной последовательностью
{ .
Ч.т.д..
.
Ч.т.д..
Лемма
5:
Любая сходящаяся последовательность имеет только одну предельную точку.
Доказательства:
пусть
имеет только одну предельную точку.
Доказательства:
пусть
 сходится к числу a,
точка по определению является предельной
точкой последовательности. Действительно,
для сходящейся последовательности для
любого
сходится к числу a,
точка по определению является предельной
точкой последовательности. Действительно,
для сходящейся последовательности для
любого
 ;
;
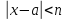 ;
;
 .
Таким образом, число a
является
предельной точкой
.
Таким образом, число a
является
предельной точкой
 .
Предположим, что существует еще одна
предельная точка b,
тогда
в соответствии с леммой 4 из
.
Предположим, что существует еще одна
предельная точка b,
тогда
в соответствии с леммой 4 из
 можно выбрать подпоследовательность
{
можно выбрать подпоследовательность
{ ,
сходящуюся к b.
В соответствии со свойствами
подпоследовательности любая
подпоследовательность сходящейся к a
последовательности
,
сходящуюся к b.
В соответствии со свойствами
подпоследовательности любая
подпоследовательность сходящейся к a
последовательности
 сходится к a.
Следовательно, a=b
и
последовательность
сходится к a.
Следовательно, a=b
и
последовательность
 имеет только одну предельную точку.
Ч.т.д.
имеет только одну предельную точку.
Ч.т.д.
Верхний
и нижний пределы последовательности
(определение). Определение:
наибольшее
 (наименьшее
(наименьшее
 )
предельное значение последовательности
)
предельное значение последовательности
 называется верхним (нижним) пределом
этой последовательности.
называется верхним (нижним) пределом
этой последовательности.

Теорема
21 о вложенных, стягивающихся отрезках.
Определение:
Пусть
 ,
,
 ,…,
,…, бесконечные множества отрезков, каждый
из которых, начиная со второго, содержится
в предыдущем. И пусть
бесконечные множества отрезков, каждый
из которых, начиная со второго, содержится
в предыдущем. И пусть
 при
при
 .
Тогда существует единственная точка
c,
принадлежащая
сразу всем отрезкам. Доказательства:
Докажем, что может существовать только
одна точка, принадлежащая всем отрезкам.
Предположим, что существует еще одна
точка d,
принадлежащая всем отрезкам. Тогда и
весь отрезок cd
принадлежит отрезкам и выполняется
.
Тогда существует единственная точка
c,
принадлежащая
сразу всем отрезкам. Доказательства:
Докажем, что может существовать только
одна точка, принадлежащая всем отрезкам.
Предположим, что существует еще одна
точка d,
принадлежащая всем отрезкам. Тогда и
весь отрезок cd
принадлежит отрезкам и выполняется
 .
Но это противоречит
.
Но это противоречит
 => существует только одна точка. Нетрудно
увидеть, что
=> существует только одна точка. Нетрудно
увидеть, что
 является неубывающей и ограниченной
сверху, хотя бы числом
является неубывающей и ограниченной
сверху, хотя бы числом
 .
В свою очередь последовательность {
.
В свою очередь последовательность { }
является невозрастающей и ограниченной
сверху. Тогда по теореме о сходимости
монотонной последовательности и
}
является невозрастающей и ограниченной
сверху. Тогда по теореме о сходимости
монотонной последовательности и
 , и {
, и { }
сходятся. Более того, их пределы одинаковы.
}
сходятся. Более того, их пределы одинаковы.
 .
При этом с
является
точкой верхней (нижней) гранью
последовательности
.
При этом с
является
точкой верхней (нижней) гранью
последовательности
 (
( .
.
 ,ч.т.д.
,ч.т.д.
Теорема
22 (Больцано-Вейерштрасса).
Теорема:
Из любой ограниченной последовательности
можно выбрать сходящуюся подпоследовательность.
Доказательства:
Так как последовательность
 .
Получим подпоследовательность следующим
образом. Разобьем
.
Получим подпоследовательность следующим
образом. Разобьем
 на две части. Тогда в одной из половинок
(пусть это будет
на две части. Тогда в одной из половинок
(пусть это будет
 )
содержится
)
содержится
 .
Выберем некоторый элемент
.
Выберем некоторый элемент
 .
Далее разделим
.
Далее разделим
 на две половинки. Пусть в полученном
отрезке содержится бесконечно много
элементов
на две половинки. Пусть в полученном
отрезке содержится бесконечно много
элементов
 .
Выберем некоторый элемент
.
Выберем некоторый элемент
 .и
т.д. Получим последовательность
.и
т.д. Получим последовательность
 ,
где
,
где
 .
Множество построенных отрезков – это
множество вложенных стягивающихся
(
.
Множество построенных отрезков – это
множество вложенных стягивающихся
( =
= ).
Тогда
).
Тогда
 .
Тогда по теореме о двух милиционерах
последовательность
.
Тогда по теореме о двух милиционерах
последовательность
 сходится к числу c.
сходится к числу c.
Теорема23(о существовании у ограниченной последовательности предельных точек и следствия) Всякая ограниченная последовательность имеет хотя бы одно предельное значение. Док-во. В соответствии с теоремой Больцано-Вейерштрасса в любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. В соответствии со 2-м определением этот предел является предельной точкой исходной последовательности.
-
Для любого ε>0 интервал (
 -
ε,
-
ε,
 ε) содержит все элементы ограниченной
последовательности с некоторого номера.
Иначе вне этого интервала содержится
конечное число этой последовательности.
ε) содержит все элементы ограниченной
последовательности с некоторого номера.
Иначе вне этого интервала содержится
конечное число этой последовательности. -
Любой интервал (а, b), вне которого находится конечное число элементов ограниченной последовательности, содержит в себе интервал ((


Понятие фундаментальной последовательности.
Последовательность
{ }
называется фундаментальной, если для
любого ε>0 найдется номер N(ε)
такой, что при n≥
N(ε)
и для любого натурального ряда p(p=1,2,3…)
выполняется неравенство
}
называется фундаментальной, если для
любого ε>0 найдется номер N(ε)
такой, что при n≥
N(ε)
и для любого натурального ряда p(p=1,2,3…)
выполняется неравенство
 <ε
<ε
Теорема24(о сходимости ограниченной последовательности с совпадающими нижним и верхним пределами.)
Для
того, чтобы последовательность { }
была сходящейся, необходимо и достаточно,
чтобы она была ограничена и чтобы ее
верхний
}
была сходящейся, необходимо и достаточно,
чтобы она была ограничена и чтобы ее
верхний
 и нижний
и нижний
 пределы совпадали(
пределы совпадали(
Док-во.
Необходимость-считается, что
последовательность { }
является сходящейся. Надо доказать, что
она ограничена или
}
является сходящейся. Надо доказать, что
она ограничена или
 в соответствии со свойством(теорема8)
сходящаяся последовательность ограничена.
А в соответствии с леммой5 сходящаяся
последовательность имеет лишь одну
предельную точку, совпадающую с пределом
последовательности, т.е.
в соответствии со свойством(теорема8)
сходящаяся последовательность ограничена.
А в соответствии с леммой5 сходящаяся
последовательность имеет лишь одну
предельную точку, совпадающую с пределом
последовательности, т.е. Достаточность-считается, что
последовательность {
Достаточность-считается, что
последовательность { }
ограничена и
}
ограничена и
 .
Надо доказать, что {
.
Надо доказать, что { }
сходится. Выберем произвольное ε>0, и
воспользуемся следствием1 из теоремы23.
В соответствии с этим следствием интервал
интервал (
}
сходится. Выберем произвольное ε>0, и
воспользуемся следствием1 из теоремы23.
В соответствии с этим следствием интервал
интервал (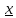 -
ε,
-
ε,
 ε) содержит все элементы последовательности,
начиная с некоторого номера, т.е. этот
интервал содержит бесконечно много
элементов последовательности {
ε) содержит все элементы последовательности,
начиная с некоторого номера, т.е. этот
интервал содержит бесконечно много
элементов последовательности { }.
Т.к.
}.
Т.к.
 ,
то этот интервал запишем в виде: (a-
ε,
,
то этот интервал запишем в виде: (a-
ε,
 ε). Этот интервал есть ε-окрестность
точки a.
он содержит бесконечно много элементов
последовательности {
ε). Этот интервал есть ε-окрестность
точки a.
он содержит бесконечно много элементов
последовательности { }.
Тогда в соответствии с 1-м определением
предельной точки, число а является
предельной точкой этой последовательности.
Т.к.
}.
Тогда в соответствии с 1-м определением
предельной точки, число а является
предельной точкой этой последовательности.
Т.к.
 то последовательность {
то последовательность { }.
Является сходящейся.
}.
Является сходящейся.
Критерий Коши сходимости числовой последовательности(теорема25).
Для
того, чтобы последовательность { }
сходилась, необходимо и достаточно,
чтобы она была фундаментальна.
}
сходилась, необходимо и достаточно,
чтобы она была фундаментальна.
Необходимость-считается,
что последовательность { }
сходится. Надо доказать, что она является
фундаментальной. По определению сход.
последовательности для любого ε найдется
N(ε)
такой, что
}
сходится. Надо доказать, что она является
фундаментальной. По определению сход.
последовательности для любого ε найдется
N(ε)
такой, что
 <
ε, n≥
N(ε).
Номера n+p>n,
поэтому при n≥
N(ε)
выполняется неравенство
<
ε, n≥
N(ε).
Номера n+p>n,
поэтому при n≥
N(ε)
выполняется неравенство
 <ε
оценим
<ε
оценим
 .
.
 =
= ≤
≤ +
+ <2ε.
<2ε.
 <
ε при n≥
N(ε).
<
ε при n≥
N(ε).
Достаточность-считается,
что последовательность фундаментальная,
надо доказать, что она сходится.
Воспользуемся теоремой 24. Надо доказать,
что фундаментальная последовательность
ограничена и
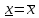 .
Ограниченность последовательности
очевидна, т.к. выполняется
.
Ограниченность последовательности
очевидна, т.к. выполняется
 <
ε, при n≥
N(ε)
и любом p.
<
ε, при n≥
N(ε)
и любом p.
 <
ε ->
<
ε ->
 ε<
ε< <
< ε. A=max
{x1,
x2,
…xn-1,
xn+ε},
тогда для всех n
выполняется
ε. A=max
{x1,
x2,
…xn-1,
xn+ε},
тогда для всех n
выполняется
 <A.
В соответствии с ним интервал (
<A.
В соответствии с ним интервал ( ε,
ε,
 ε) содержит в себе интервал (
ε) содержит в себе интервал ( )
т.е. выполняется неравенство
)
т.е. выполняется неравенство
 ≤
≤ ε-(
ε-( ε)=2ε.
ε)=2ε.
 <2ε,
=>
<2ε,
=>
 ,
тогда по теореме24 фундаментальная
последовательность является сходящейся.
,
тогда по теореме24 фундаментальная
последовательность является сходящейся.
Понятие производной функции, ее геометрический смысл.
Производной
функции y’(x),
f’(x)
называется
предельное
значение приращения функции к приращению
аргумента

Геометрический смысл-tg угла наклона касательной к графику функции.
Правая и левая производные.
Правой(левой)
производной функции y=f(x)
называется правое(левое) предельное
значение отношения приращения функции

F’(x+0) правая производная, F’(x-0) левая производная.
Дифференцируемость функции(определение. Теорема26).
Функция называется дифференцируемой в т. X, если ее приращение Δy ( в этой точке), соответствующее приращению аргумента Δx, равно Δy=A* Δx+o(Δx) не зависит от Δx.
Для того, чтобы функция была дифференцируемой в точке x0 необходимо и достаточно, чтобы она имела этой точке конечную производную.
Необходимость-считается,
что функция дифференцируема в точке
x0.
Надо доказать, что она имеет в этой точке
производную. По определению дифференциала
функции Δy= =>
=>
 =A+
=A+
 ,
,
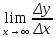 =A+
=A+ =A,
y’(x0)=A.
Δy0=y’(x0)+o(
=A,
y’(x0)=A.
Δy0=y’(x0)+o( )
)
Достаточность-считается,что
в т. x0
существует конечная производная. Надо
доказать, что в x0
функция дифференцируема. По определению
производной
 =f’(x),
тогда
=f’(x),
тогда
 – y’(x0)=α(
– y’(x0)=α( =
α(
=
α( ,
,
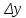 =y’(x0)*
=y’(x0)* +o(x)
+o(x)
Дифференциал функции.
Дифференциалом функции dy в точке x0 называется главное приращение функции в этой точке dy=y’(x)*dx
Правила дифференцирования суммы, разности, произведения частного(теорема27).
Пусть функции u(x) и g(x) дифференцируемы в точке x. Тогда сумма, разность, произведение, частное(при условии, что знаменатель ≠0 в точке x) этих функций также дифференцируемы. При этом справедливы формулы:
-
 .
. -
 .
. -
 .
.
Дифференцирование обратной функции(теорема28)
Пусть
функция y=f(x)
дифф. в точке x0
и
пусть в окрестности этой точки y=f(x)
имеет обратную функцию x=f-1(y).
Тогда обратная функция дифф. в точке y0
=f(x0)(соответствует
т. X0)
и справедлива формула:
 (y0)=
(y0)= =
=
Док-во.
Возьмем некоторое приращение аргумента
y,
т.е.
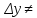 0.
Тогда соответствующее приращение
0.
Тогда соответствующее приращение
 (в
силу строгой монотонности обратной
функции). Производная обратной функции
(в
силу строгой монотонности обратной
функции). Производная обратной функции
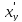 (y0)=
(y0)= =
=
 =
=
Производные показательной и обратных тригонометрических функций.
-
y=ax (a>0, a≠0, x (-∞, +∞)) x=logay обратная функция. y’=[ax]x’=
 =
= =ylna=axlna
=ylna=axlna -
y=arcsinx (x [-1, 1], y [
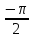 ,
,
 ])
x=siny, y’=[arcsinx]’=
])
x=siny, y’=[arcsinx]’= =
=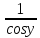 .
Используя
основное тригонометрическое тождество:
sin2y+cos2y=1
=> cosy=+-
.
Используя
основное тригонометрическое тождество:
sin2y+cos2y=1
=> cosy=+- ,
cosy=
,
cosy= ,
тк y
[
,
тк y
[ ,
,
 ].
].
 =
= =
= .
По
аналогии ищутся другие производные.
.
По
аналогии ищутся другие производные. -
Y=arctg x; (x (-∞, ∞), y (
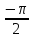 ,
,
 )),
x=tg x. y’=[arctg x]’=
)),
x=tg x. y’=[arctg x]’= =cos2y=(1+tg2y=
=cos2y=(1+tg2y= )=
)=
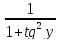 =
= .
[arctg x]’=
.
[arctg x]’= .
.
Правило дифференцирования сложной функции(теорема29).
Рассмотрим
сложную функцию вида y=f(g(x)).
Пусть функция g(x)
дифференцируема в точке x0
,
а функция f(g)
дифференцируема в точке g0=g(x).
Тогда сложная функция y=f(g(x))
дифференцируема в точке x0
,
при этом справедлива формула
 *
* (без
доказательства).
(без
доказательства).
Логарифмическая производная.
Пусть
функция y=f(x)
дифференцируема в точке x
и положительна в ней. Тогда имеет смысл
равенство ln
y=ln
f(x),
(ln
y)’=(ln(f(x)))’
=>
 => y’=y(ln
f(x))’;
логарифмическая производная применяется
при вычислении производной функции
вида y=
=> y’=y(ln
f(x))’;
логарифмическая производная применяется
при вычислении производной функции
вида y=
Использование дифференциала для приближенных вычислений.
Пусть
функция y=f(x)
дифференцируема в точке x0,
тогда приращение Δy=f’(x) при x<<1
можно заменить Δy
на dy
(Δy≈dy=f’(x0)Δx).
y(x0
+
Δx)-y(x0)
≈f’(x)dx,
y(x0
+
Δx)
≈ y(x0)+
f’(x0)dx
при x<<1
можно заменить Δy
на dy
(Δy≈dy=f’(x0)Δx).
y(x0
+
Δx)-y(x0)
≈f’(x)dx,
y(x0
+
Δx)
≈ y(x0)+
f’(x0)dx
Производные и дифференциалы высших порядков. Формула Лейбница.
Пусть функция y=f(x) дифференцируема в точке x, тогда y’=f’(x)=g(x). Если g(x) дифференцируема в той же точке, можно записать g’(x)=[f’(x)]’=f’’(x). Рассуждая аналогично, можно ввести поняти3,4,… n-порядок производных.
Для производной n-го порядка принято следующее обозначение y(n)=f(n)(x).
Формула Лейбница.
Y=u(x)*v(x).
(uv)(n)=
Дифференциал высшего порядка. Пусть функция y=f(x) дифференцируема в точке x. dy=f’(x)dx. Если функция f’(x) дифференцируема, то можно записать d(dy)=d2y=d(f’(x)dx)=d(f’(x)dx=f’’(x)dxdx=f’’(x)(dx)2
Если
функция n-раз
дифференцируема, то можно записать
dny=f(n)(x)(dx)n=f(n)(x)=
Дифференцирование
функции, заданной параметрически. ,
,

Правило
Лопиталя(теорема30). Пусть
функция f(x)
и g(x)
определены и дифференцируемы в некоторой
окрестности точки x0,
пусть кроме того,
 =
= =0,
=0,
 =
= =∞
и производная g’(x)
отлична от 0 в рассматриваемой окрестности.
Тогда если существует предельное
значение
=∞
и производная g’(x)
отлична от 0 в рассматриваемой окрестности.
Тогда если существует предельное
значение
 ,
то существует и предельное значение
,
то существует и предельное значение
 и справедливо равенство:
и справедливо равенство:
 =
=
 .
Замечание-если
условие теоремы выполняется для f’(x)
и g’(x),
то справедливо
.
Замечание-если
условие теоремы выполняется для f’(x)
и g’(x),
то справедливо
 =……
=…… .
Данное правило используется для раскрытия
неопределенностей вида
.
Данное правило используется для раскрытия
неопределенностей вида
 ,
,
 ,
,
 .
.
Формула Тейлора(теорема31).
Пусть функция у=f(x) дифференцируема n-раз в точке x0 и некоторой окрестности этой точки. Тогда для любой точки x из этой окрестности справедлива формула:
f(x)=f(x0)+ +
+ +…+
+…+ +
+ ,
остаточное слагаемое.
,
остаточное слагаемое.
В
форме Пеана o((x-x0)’),
в форме Лагранжа
 *
* .
.
Частный вид формулы Тейлора при x0 носит название формулы Маклорена.
Формула Маклорена для некоторых элементарных функций.




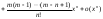

Схема построения графика функции.
Для построения графика функции y=f(x) необходимо определить:
1)область допустимых значений аргумента функции. Четность, нечетность. Периодичность.
2)Асимптоты: а)вертикальные б)наклонные
3)область возрастания и убывания функции. Точки экстремумов.
4)направление выпуклости. Точки перегиба.
5)Точки пересечения с осями координат.
Асимптоты.
Определение:
прямая х=х0 называется вертикальной
асимптотой графика функции y=f(x),если
выполняется хоть одно из условий: или
или
 ;
;
Определение:
Прямая y=kx+b
называется наклонной асимптотой графика
функции y=f(x)
при х--> (х-->-
(х-->- ,если
эта функция представима в виде y=kx+b+α(x)
где α(x)0
при x
,если
эта функция представима в виде y=kx+b+α(x)
где α(x)0
при x (-
(- .
.
Теорема
32 о необходимом и достаточном условии
наличия наклонной асимптоты :
для того чтобы функция y=f(x)
имела наклонную асимптоту при x (-
(- необходимо и достаточно, чтобы существовали
пределы:
необходимо и достаточно, чтобы существовали
пределы:


Док-во
: Необходимость: предполагается, что
график функции y=f(x)имеет
наклонную асимптоту: надо доказать, что
выполняются соотношения:
 По
определению, если функция имеет наклонную
асимптоту y=kx+b,
при х-->
По
определению, если функция имеет наклонную
асимптоту y=kx+b,
при х--> ,то
справедливо представление этой функции
в виде:
,то
справедливо представление этой функции
в виде: =
= =
= +
+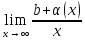 =k.
=k. =
= α(x)-kx)=
α(x)-kx)=
 α(x))=b-
α(x))=b- α(x))=b.
Достаточность: предполагается, что
выполняются равенства:
α(x))=b.
Достаточность: предполагается, что
выполняются равенства:
 Надо
доказать, что y=kx+b
является наклонной асимптотой Графика
функции y=f(x),
при х-->
Надо
доказать, что y=kx+b
является наклонной асимптотой Графика
функции y=f(x),
при х--> .воспользуемся
вторым равенством.Док-во :Наличие предела
у функции f(x)-kx
означает, что f(x)-kx-b=
α(x).где
α(x)
–бесконечно малая при x
.воспользуемся
вторым равенством.Док-во :Наличие предела
у функции f(x)-kx
означает, что f(x)-kx-b=
α(x).где
α(x)
–бесконечно малая при x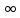 функция. Следовательно:f(x)=kx+b+
α(x).
функция. Следовательно:f(x)=kx+b+
α(x).
