Алгоритм вычисления дисперсии

Для нахождения дисперсии D данных х₁, х₂, …, х_n измерения следует вычислить:

1) среднее значение ;

2) отклонения данных от М, т.е. ;

3) квадраты отклонений отклонений, найденных на предыдущем шаге;

4) среднее значение всех квадратов отклонений – это и есть дисперсия D:

;

- стандартное отклонение.

Свойства дисперсии

1) Дисперсия постоянной величины равна нулю:

D(С) = 0.

2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

D(С·Х) = С²·D(Х).

3) Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:

D(Х₁ + Х₂ + ... + Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n).

4) Дисперсия разности независимых случайных величин равна сумме дисперсий слагаемых:

D(Х₁ - Х₂ - ... - Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n).

Определение. Случайная величина, у которой математическое ожидание равно 0, а дисперсия равна 1, называется стандартной или стандартизированной случайной величиной.

Если имеется СВ Х с математическом ожиданием (читается «мю») и стандартным отклонением. Тогда случайная величина

является стандартной случайной величиной.

7. Коэффициент вариации

Коэффициент вариации случайной величины Х (обозначается илиVar(X) ) - это относительная мера вариации:

V(X) = .

Оценка интенсивности вариации состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив.

Моменты распределения и показатели его формы. Центральные моменты распределения

Математическое ожидание и дисперсия являются частными случаями более общих понятий – моментов СВ.

Определение. Начальным моментом порядка k СВ Х называется математическое ожидание k-й степени этой величины. Начальный момент порядка k обозначается .

Таким образом, по определению,

.

Для дискретной СВ начальный момент выражается суммой:

.

В частности, , т.е. начальный момент первого порядка есть математическое ожидание.

Определение. Центральным моментом порядка k СВ Х называется математическое ожидание величины (Х – М(Х)). Центральные моменты обозначаются через(читается – мю).

Таким образом, по определению,

.

В частности,

,

т.е. центральный момент второго порядка есть дисперсия.

При этом:

.

Для дискретной СВ:

.

Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядка, называемые соответственно коэффициентами асимметрии и эксцесса.

9. Коэффициент асимметрии

Асимметрия (коэффициент асимметрии) случайной величины (и дискретной, и непрерывной) As(X) - величина, характеризующая степень «скошенности» распределения относительно математического ожидания.

Определение. Коэффициентом асимметрии (коэффициентом «скошенности») дискретной случайной величины Х называется величина Аs(X), вычисляемая по формуле:

.

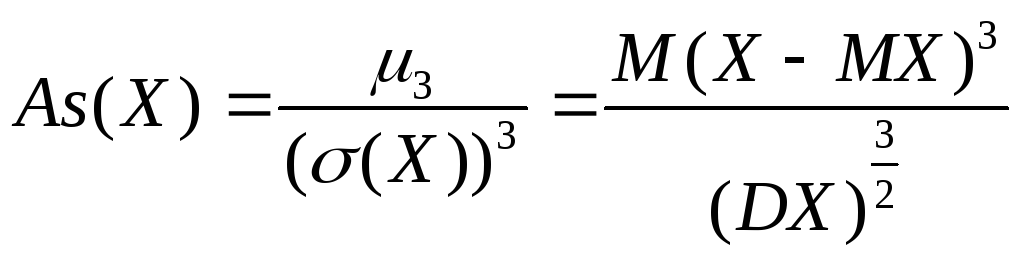Если коэффициент асимметрии (отрицателен), то либо большая часть значений случайной величины, либомода находятся левее математического ожидания. В этом случае кривая распределения более полога слева от МоХ.

Если коэффициент асимметрии , то правее. В этом случае кривая распределения более полога справа отМоХ.

Если распределение по форме близко нормальному закону, то медиана находится между модой и средней величиной, причем ближе к средней, чем к моде.

При правосторонней асимметрии:

.

При левосторонней асимметрии:

.

Для умеренно асимметричных распределений справедливо равенство:

.