
II семестр
Механические колебания и волны
Общая черта колебательных процессов – высокая степень повторяемости процесса.
Колебания подразделяются:
-
по природе: механические, электромагнитные;
-
по степени повторяемости: периодические, непериодические;
-
по свойствам: гармонические, ангармонические;
-
по способу возникновения: свободные, вынужденные.
Механические колебания
Колебательные системы
Колебания – физические процессы, которые происходят с определённой повторяемостью во времени.
Периодические колебания – колебания, при которых значения характерных параметров системы повторяются через равные промежутки времени.
Полное колебание – процесс, проходящие в системе за период.
Период – минимальный период времени, через который все параметры системы повторяются.
Частота – число полных колебаний, происходящих в единицу времени.
Циклическая частота – число
полных колебаний за
![]() единиц времени.
единиц времени.
Гармонические колебания – колебания, происходящие по закону изменения гармонических функций.
Линейные колебания – колебания, возникающие в линейных системах.
Линейная система – система, реакция которой линейно зависит от воздействия.
Свободные (собственные) колебания – колебания, которые происходят в отсутствие внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы из состояния её устойчивого равновесия под действием внутренних сил системы.
Вынужденные колебания – колебания, возникающие в какой-либо системе под влиянием переменного внешнего воздействия.
Равновесие в механических системах и возникновение колебаний
Условие равновесия точечного
тела:
![]() ,
протяжённого тела:
,
протяжённого тела:
![]() ,
,
![]() .
.
Характерным свойством колебательной системы является наличие возвращающей (квазиупругой) силы.
![]() ,
,
![]() ;
;
![]() .
Необходимое условие колебательной
системы:
.
Необходимое условие колебательной
системы:
![]() .
Достаточность:
.
Достаточность:
![]() .
.
Свободные незатухающие колебания
у
Пружинный маятник:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() .
.
Математический маятник:
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() .
.
Физический маятник:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где![]() .
.
Приведённая длина физического
маятника – длина математического
маятника, период колебаний которого
равен периоду колебаний физического
маятника,
![]() .
.
Центр качания – математическая точка, отстоящая от точки подвеса на приведённую длину и лежащая на маятнике.
Если физический и математический маятники с приведённой длиной колеблются около одной оси, то материальная точка математического и центр качания физического маятника движутся синхронно, если вначале их отклонили на одинаковый угол и одновременно отпустили.
Точка подвеса и центр качания обратимы (можно подвесить за любую из них, период колебаний будет одинаков).
Уравнение колебаний
Все системы описываются
уравнением
![]() ,
где
,
где
![]() (пружинный),
(пружинный),
![]() (математический),
(математический),
![]() (физический).
(физический).
Переменная колебаний – параметр, характеризующий отклонение системы от положения равновесия. (x).
Решение уравнения колебаний.
![]() .
.
Линейный гармонический осциллятор – любая колебательная система, в которой возникают малые линейные гармонические колебания.
Основные характеристики гармонических колебаний
Амплитуда – максимальное
значение переменной колебания
(максимальное отклонение системы от
положения равновесия). Амплитуда всегда
положительна.
![]() ,
A
– амплитуда.
,
A
– амплитуда.
Фаза – параметр, характеризующий
относительное значения отклонения
системы от положения равновесия (![]() ).
).
Начальная фаза – значение
фазы в начальный момент времени (![]() ).
).
Период:
![]() ,
частота
,
частота
![]() ,
,
![]() - циклическая частота.
- циклическая частота.
Свойства гармонических колебаний:
-
Частота и период гармонических колебаний определяются свойствами самой системы.
-
Амплитуда и начальная фаза зависят от способа возбуждения колебаний.
-
Период и частота не зависят от амплитуды.
Скорость и ускорение при колебаниях:
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]() .
.
Начальные условие – задание смещение и скорости в начальный момент времени.
-
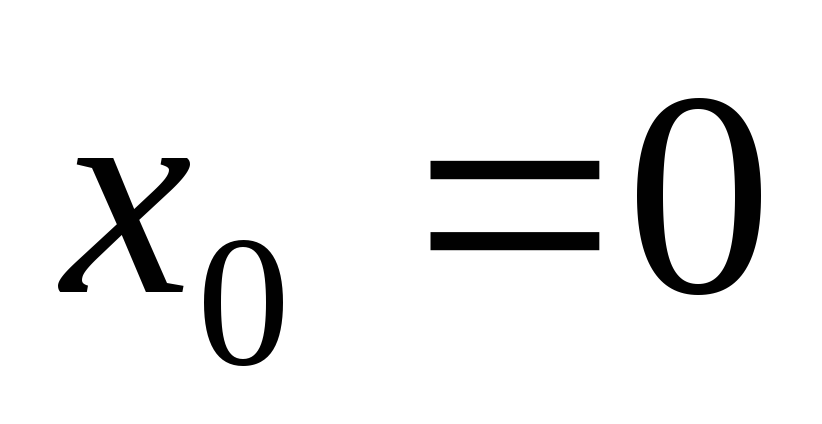 ,
,
 ,
,
 - колебания отсутствуют.
- колебания отсутствуют. -
 ,
,
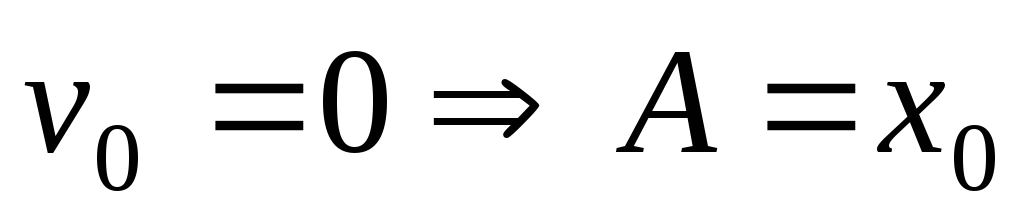 ,
,
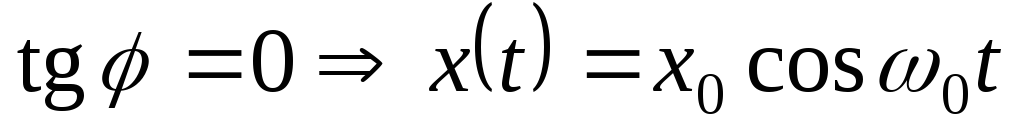 .
. -
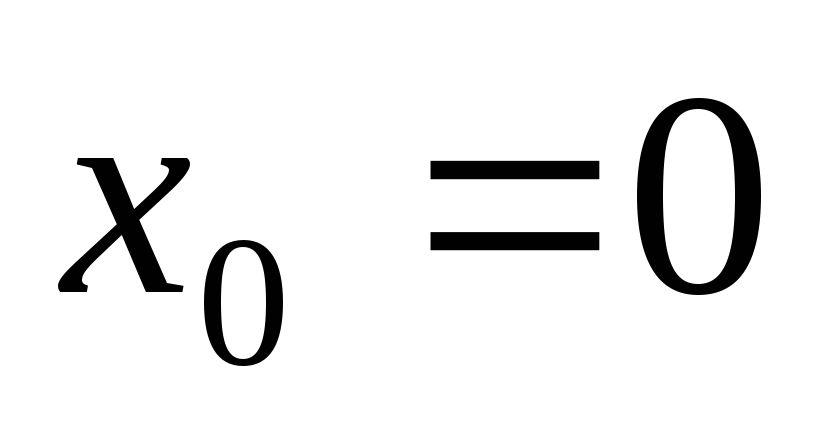 ,
,
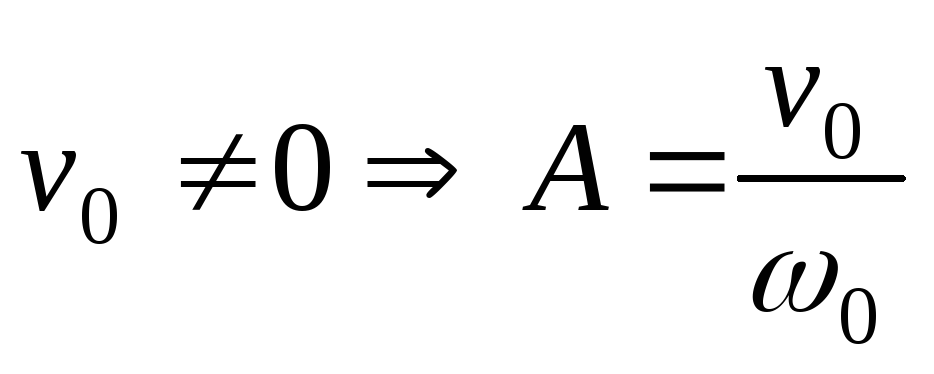 ,
,
 .
. -
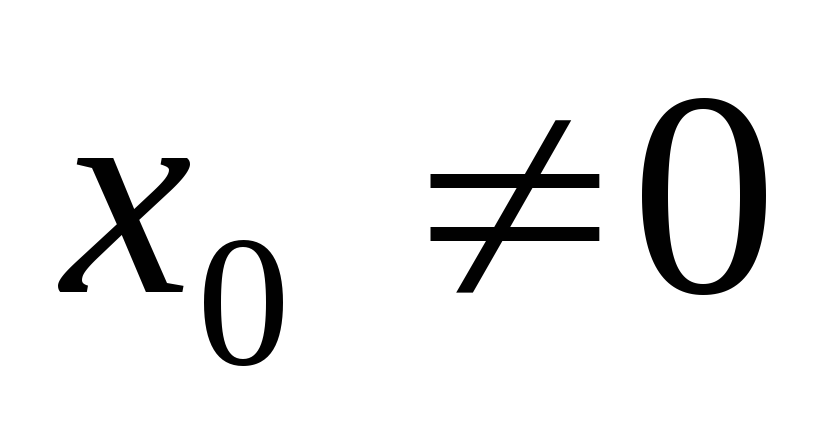 ,
,
 ,
,
 .
.
Задание начальных условий определяет амплитуду и начальную фазу.
Кинетическая и потенциальная энергия системы:
![]() .
Для пружинного маятника
.
Для пружинного маятника
![]()
![]() - закон сохранения энергии при свободных
незатухающих колебаниях.
- закон сохранения энергии при свободных
незатухающих колебаниях.
![]() .
.![]() ,
,
![]() .
.
Э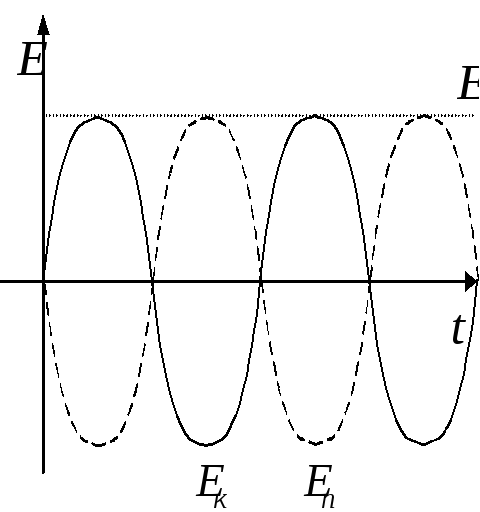 нергия
и вычисление периода колебаний:
нергия
и вычисление периода колебаний:
-
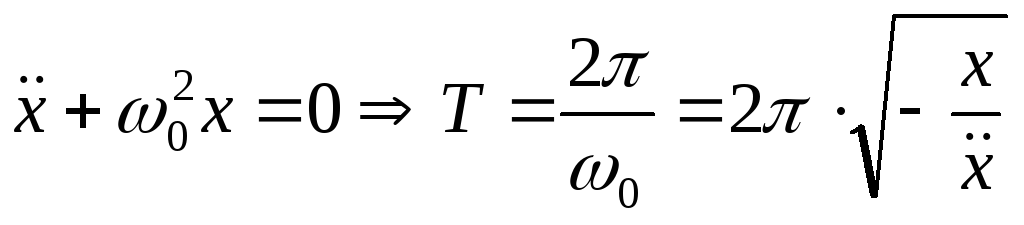 .
.

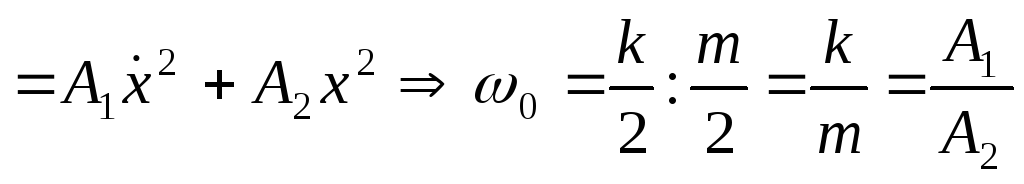 .
. -
Пружинный маятник:
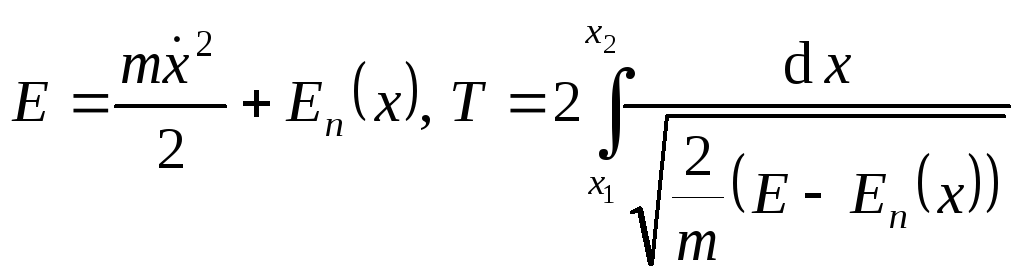 .
.

-
Математический маятник:
 /
/
Представление колебаний с помощью векторных диаграмм и комплексных чисел.
П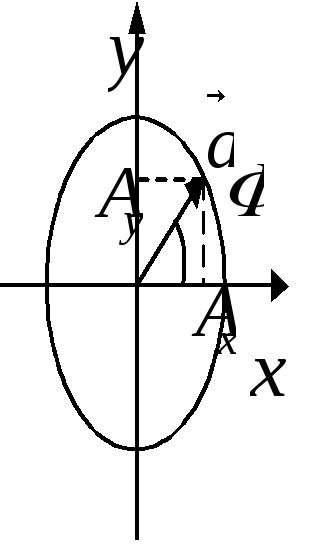 усть
усть
![]() ,
где
,
где
![]() .
Возьмём
.
Возьмём
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
а уравнение
,
а уравнение
![]() описывает движение проекций конца
вектора по соответствующим осям. Пусть
теперь xy
– комплексная плоскость. Тогда
описывает движение проекций конца
вектора по соответствующим осям. Пусть
теперь xy
– комплексная плоскость. Тогда
![]() .
.
Фазовая плоскость
(пространство) – геометрический образ,
представимый множеством состояний
системы
![]() или
или
![]() .
.
Фазовая точка – точка фазовой плоскости, определяемая скоростью и координатой и соответствующая определённому состоянию системы.
Фазовая траектория – линия, которую описывает точка на фазовой плоскости при изменении состояния системы.
Фазовый портрет маятника
– фазовая траектория маятника:
![]() или
или
![]() (
(![]() или
или ![]() ).
).
Ф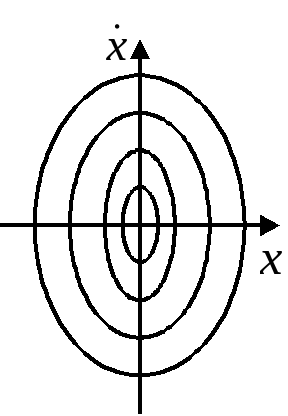 азовый
портрет для гармонических колебаний:
азовый
портрет для гармонических колебаний:
![]() .
.
