12.2. Лабораторная работа 2 Частотный анализ типовых звеньев.

Цель работы: освоение методов анализа линейных систем с помощью программы Vissim; изучение частотных характеристик типовых линейных звеньев.

Задание к работе: 1. Записать выражения для W(jw), ,,, с учетом коэффициентов вашего варианта для каждого из трех типовых динамических звеньев.

2. Построить графики АЧХ, ЛАЧХ, ФЧХ, ЛФЧХ и АФЧХ (годограф Найквиста) для каждого их трех типовых динамических звеньев. Изучить влияние параметров звена на общий вид графиков. Указать на графиках и записать координаты точек сопряжения и среза. На графике АФЧХ указать направление обхода.

3. Записать передаточную функцию для заданного дифференциального уравнения. Построить для нее ЛАЧХ, ЛФЧХ и АФЧХ.

4. Сделать вывод о проделанной работе.

Вводная часть:

Переход от передаточной функции W(s) к комплексному коэффициенту передачи W(jw)

где действительная часть комплексного числаRe(W(jw));

мнимая часть комплексного числа Im(W(jw)).

Частотные характеристики любого звена или системы:

АЧХ:

ФЧХ:

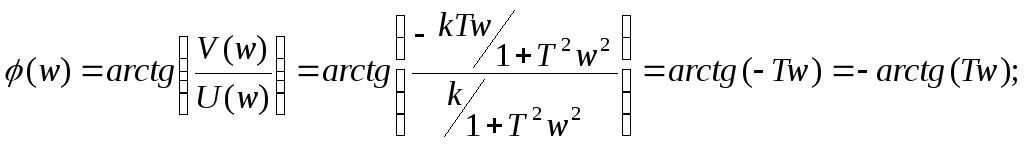
ЛАЧХ:

ЛФЧХ:

() = arg(W(j)),  [рад];

АФЧХ (годограф Найквиста):

Это геометрическое место точек, которые описывает конец вектора частотной передаточной функции, при изменении частоты от -∞ до +∞. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка.

Пример выполнения работы:

1. Апериодическое звено 1-го порядка.

1. Записать комплексный коэффициент передачи (ККП) апериодического звена

, где k=2; T=0.2 c.

1.2. Записать выражение для АЧХ, ФЧХ, ЛАЧХ.

АЧХ:

ФЧХ:

ЛАЧХ:

1.3. На рабочем поле собрать схему, состоящую из генератора ступенчатого сигнала, апериодического звена и осциллографа, получить график переходного процесса.

1.4. Построить ЛАЧХ и ЛФЧХ апериодического звена.

Для этого необходимо выделить звено или систему звеньев, для которых строятся частотные характеристики, а затем выбрать пункт меню Analyze – Frequency Response. Полученные окошки необходимо растянуть и расположить одно под другим. Далее щелкнув два раза по каждому окошку на вкладке свойства задать координатную сетку, подписать название диаграмм, координатных осей, единиц измерения и диапазон изменения величин.

На полученных характеристиках дорисовать асимптотические графики и полученный результат вставить в отчет.

Пример ЛАЧХ и ЛФЧХ апериодического звена изображен на картинке.

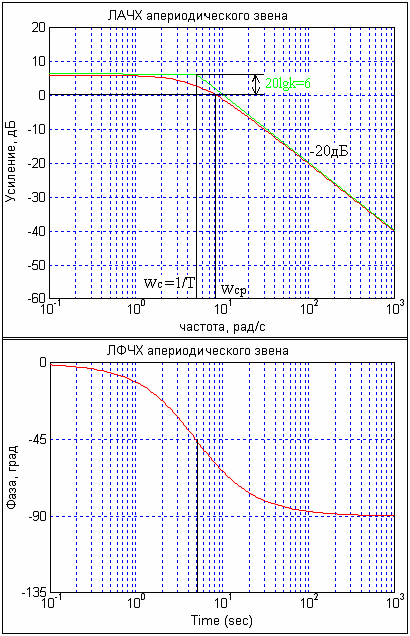
1.5. По графику определить частоту сопряжения (точки излома или перегиба), частоту среза (пересечение ЛАЧХ с осью 0 дБ) и коэффициент усиления. Убедиться, что они соответствуют заданным параметрам.

1.6. Изменить значение сначала коэффициента усиления, а потом постоянной времени и посмотреть, как это отразиться на частотных характеристиках.

1.7. Все полученные графики вставить в отчет и под каждым сделать соответствующие выводы.

ω_ср=8 рад/с

ω_с=5 рад/с (ω_c=1/T=1/0.2=5)

k=10^6/20=1.99≈2

1.8. Построить амплитудно-фазовую частотную характеристику АФЧХ (или годограф Найквиста) для апериодического звена 1-го порядка.

Для чего необходимо выделить звено и выбрать пункт меню Analyze – Nyquist Response.

На графике указать направление обхода контура, т.е. направление движения при изменение частоты от 0 до +∞.

2. Проделать тот же анализ для двух других звеньев.

3. Самостоятельно найти выражение для передаточной функции заданного дифференциального уравнения.

4. Построить ЛАЧХ, ЛФЧХ и АФЧХ для полученной передаточной функции.

5. Оформить отчет и сделать вывод о проделанной работе.

Общий вид дифференциального уравнения:

№ вар.	а1	а2	а3	а4	а5	а6	b1	b2	b3	b4	b5
1	4	-	-6	-2	-	5	1	-	-3	6	4
2	-	3	-5	-	2	1	-	3	-4	-	7
3	3	5	4	-1	-	3	4	5	-8	-9	6
4	-	-	7	-15	8	10	-	-	8	12	-4
5	5	6	-	-4	-	7	4	-	-3	-5	1
6	-	-	8	-9	3	4	-	-	5	-6	4
7	1	3	-4	5	-	-3	5	1	-3	2	4
8	-	6	-	4	-6	5	-	-	8	9	2
9	-	5	4	-	-8	-2	-	7	-5	3	1
10	1	3	-4	1	2	5	7	2	-3	1	5
11	-	6	-4	-3	-	1	-	4	-5	6	-4
12	-	5	-	3	-2	4	-	6	-4	-	5
13	11	-	-	13	9	10	12	-	17	-15	20
14	-	-	8	1	9	7	-	-	6	4	12
15	3	-2	-	1	-	5	7	5	-	1	3
16	4	-	5	-	-4	2	3	-	7	-	5
17	10	-12	-	20	-	35	40	-	15	-	-25
18	-	4	5	-	3	-2	-	7	-	3	1
19	-	7	-	-9	5	1	-	4	-5	-	6
20	7	-	6	8	-	-6	5	-	-4	5	9
21	2	5	-	4	-	2	3	-	7	-	5
22	-	2	5	-	-5	3	-	4	-	6	2
23	6	-	2	5	-	-1	1	-	3	5	2
24	-	2	3	-	-6	4	-	3	-	-4	2
25	-	-	4	-5	-2	-1	-	-	7	3	5
26	1	-	6	3	-1	-1	5	-	2	-	4
27	-	3	-7	-	5	4	-	6	-	4	2
28	-	7	-	-1	-5	3	-	5	9	-	4
29	2	-	-	3	1	5	4	-	2	3	7
30	-	-	5	4	5	3	-	-	7	2	1
31	3	-5	-	-3	-	2	4	5	-	2	2
32	6	-	4	-	6	5	3	-	2	-	1
33	4	7	-	-8	-	2	3	-	5	-	-7
34	-	5	8	-	3	1	-	2	-	3	2

Контрольные вопросы:

1. Частотная передаточная функция (ПФ), частотные характеристики.

2. Методика построения асимптотических ЛАЧХ и ЛФЧХ для позиционные звеньев.

3. Методика построения асимптотических ЛАЧХ и ЛФЧХ для интегрирующих звеньев.

4. Методика построения асимптотических ЛАЧХ и ЛФЧХ для дифференцирующих звеньев.

5. Что называется частотой сопряжения.

6. Что называется частотой среза.

7. Определение годографа Найквиста.

8. Методика построения асимптотических ЛАЧХ и ЛФЧХ для произвольной линейной системы.