
- •Курсовая работа
- •Глава 1. Понятие линейной, неотрицательной и выпуклой комбинации точек плоскости и n-мерного пространства
- •1.1 Выпуклая комбинация точек
- •1.2. Линейная комбинация
- •Глава 2. Неравенство Коши- Буняковского
- •2.1 Неравенство Коши-Буняковского
- •2.2 Неравенство треугольника.
- •Глава 3. Множества связные, несвязные, ограниченные, неограниченные.
- •3.1. Множества связные несвязные
- •3.2. Множества ограниченные, неограниченные.
- •Глава 4. Замкнутость
- •Глава 5. Компактные множества.
- •5.2. Примеры компактных и некомпактных множеств
1.2. Линейная комбинация
Система уравнений вида
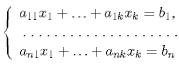 (1)
(1)
относительно
неизвестных величин
![]() ,
называется
системой линейных алгебраических
уравнений.
,
называется
системой линейных алгебраических
уравнений.
Пусть
![]() - столбцы матрицы А.
- столбцы матрицы А.
Тогда соотношения (1) равносильны равенству между векторами
![]() (2)
(2)
Выражение
![]() называется
линейной
комбинацией
называется
линейной
комбинацией
Векторов
![]() , а числа
, а числа
![]() называютсякоэффициентами
линейной комбинации.
Множество всевозможных линейных
комбинаций векторов
называютсякоэффициентами
линейной комбинации.
Множество всевозможных линейных
комбинаций векторов
![]() .
.
![]()
называется
линейной оболочкой векторов
![]() .
.
Таким образом, равенство (2) означает, что
![]() (3)
(3)
Другими словами, система (1) имеет решение (совместна) тогда и только тогда, когда правая часть b принадлежит линейной оболочке (является линейной комбинацией) столбцов матрицы коэффициентов.
Глава 2. Неравенство Коши- Буняковского
2.1 Неравенство Коши-Буняковского
Рассмотрим неравенство Коши в пространстве Rn.
Для начала дадим определение n–мерного евклидового пространства Rn
n–мерное точечное пространство, в котором расстояние между точками определено по данной формуле
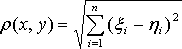 ,
,
называется n–мерным евклидовым пространством и обозначается Rn.
Ясно,
что
![]() тогда и только тогда, когдаx
= y,
т. е. когда
тогда и только тогда, когдаx
= y,
т. е. когда
![]()
при
всех i
= 1, 2, .,n.
Также ясно, что
![]() .Докажем,
что для любых трех точек
.Докажем,
что для любых трех точек![]()
![]() (2)
(2)
Это неравенство в двумерном или трехмерном пространстве выражает тот элементарный геометрический факт, что сумма двух сторон треугольника не меньше третьей стороны, и потому называется неравенством треугольника. Также
данное неравенство является одним из аксиом метрического пространства и называется аксиомой треугольника
Предварительно установим важное неравенство Коши
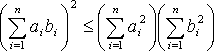 ,
(3)
,
(3)
справедливо для любых вещественных чисел ai и bi.
Простое
доказательство этого неравенства
основывается на следующем замечании:
если квадратный трехчлен Ax2+2Bx+C
с вещественными коэффициентами
неотрицателен при всех вещественных
x,
то его дискриминант
![]() *.
*.
Составим
вспомогательную функцию
![]() от вещественной переменнойx,
сводящуюся к квадратному трехчлену:
от вещественной переменнойx,
сводящуюся к квадратному трехчлену:
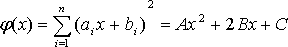 ,
,
где
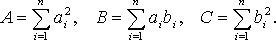
Из
определения
![]() видно, что
видно, что![]() при всехx.
при всехx.
Тогда, на основании предыдущего замечания,
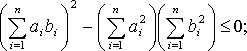
это и есть иначе записанное неравенство Коши.
Далее из неравенства (3) выведем еще одно неравенство
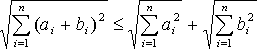 (4)
(4)
(ai
и bi
– любые вещественные числа), которое
тоже называют неравенством
Коши.
Для доказательства неравенства (4)
извлечем квадратные корни из обеих
частей неравенства (3), затем удвоив обе
части полученного нового неравенства
и прибавим к ним выражение
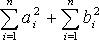
. В результате получим
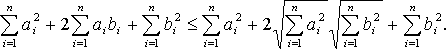
Это неравенство можно переписать и так:
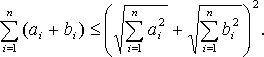
Извлекая, квадратные корни из обеих частей последнего неравенства, получим (4).Теперь уже легко доказать неравенство треугольника (2).
Пусть
![]()
Полагая в неравенстве (4)
![]()
мы получим неравенство (2).
Теперь приведем некоторые примеры метрических пространств.
Пусть множество l состоит из всех бесконечных числовых
последовательностей
![]() удовлетворяющих условию
удовлетворяющих условию
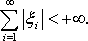
Таким образом, l – метрическое пространство
Обозначим
через l2
множества всех таких последовательностей
![]()
вещественных
чисел, для которых
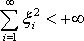 ,
и положим
,
и положим
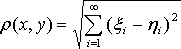 .
.
Прежде
всего нужно проверить, что
![]() конечно (т. е. что ря в правой части
сходится) для любыхx
и y
из l2.
А для этого сначала покажем, что
неравенство Коши (4) справедливо и для
бесконечных последовательностей чисел
ai
и bi
(i=1, 2, .). Действительно, беря произвольное
натуральное n,
запишем неравенство (4), а затем перейдем
в нем к пределу при
конечно (т. е. что ря в правой части
сходится) для любыхx
и y
из l2.
А для этого сначала покажем, что
неравенство Коши (4) справедливо и для
бесконечных последовательностей чисел
ai
и bi
(i=1, 2, .). Действительно, беря произвольное
натуральное n,
запишем неравенство (4), а затем перейдем
в нем к пределу при
![]() .
Получим неравенство
.
Получим неравенство
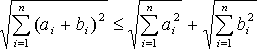 ,
(5)
,
(5)
которое мы будем называть неравенством Коши для бесконечных
последовательностей. Аналогичным образом из неравенства (3) выводится и другое неравенство Коши для бесконечных последовательностей:
 .
(6)
.
(6)
Из
неравенства (5), в частности, следует,
что если
![]()
и
![]() ,
то и последовательность
,
то и последовательность![]() ,
т.е.
,
т.е.![]() .
.
Теперь проверка выполнения в l2 аксиом метрического
пространства может быть произведена совершенно так же, как это сделано для Rn.
Пространство l2 иногда называют бесконечномерным евклидовым пространством.
