2.2 Неравенство треугольника.

Если x и y –произвольные векторы, то по

аналогии с элементарной геометрии вектор x+y естественно называть

третьей стороной треугольника, построенного на векторах x и y.

Используя неравенство Коши–Буняковского, мы получаем

или

(7)

(8)

Неравенства (7)–(8) называются неравенствами треугольника. Геометрически они означают, что длина любой стороны всякого треугольника не больше, чем сумма длин двух других сторон, и не меньше, чем абсолютная величина разности длин этих сторон.

Глава 3. Множества связные, несвязные, ограниченные, неограниченные.

3.1. Множества связные несвязные

Понятия относящиеся к множествам точек в .

Пусть -- отрезокна вещественной оси, переменная на которой обозначается буквой. Рассмотримфункций

, заданных на отрезке . Каждомусоответствует тогда точкапространства. Получаем отображение

сопоставляющее каждому соответствующую точку. Это отображениеназывается вектор-функцией, заданной на отрезке.

Пусть теперь все функции , задающие вектор-функцию, непрерывны на отрезке. Тогда и вектор-функциюбудем называть непрерывной. Для такой непрерывной вектор-функции, при изменениина отрезкеточканепрерывно перемещается из положенияв положение.

        Определение.   В описанной выше ситуации будем называть отображение

заданное формулой , непрерывным путём, или просто путём, соединяющим точкус точкойпространства.

Рис.

Множество всех точек будем называтьнепрерывной линией в , соединяющей точки и, а ту вектор-функцию, которая порождает линию-- параметризацией этой линии.     Заметим, что одна и та же линияможет иметь разные параметризации. Например, на плоскостис координатамиотрезокосиможно параметризовать, положив либо, либо(разумеется, формулы, при любомзадают ещё бесконечное множество различных параметризации той же линии).

 Определение :   Множество называется связным, если любые две точки иэтого множестваможно соединить непрерывной линией, целиком лежащей в множестве, то есть если существует путь, начинающийся ви заканчивающийся в, такой чтопри всех.

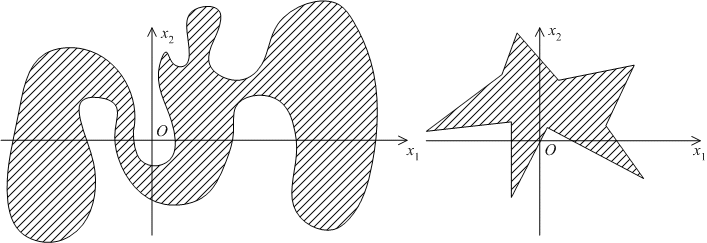
Примеры связных областей на плоскости.

Связными областями являются:

1) всё пространство ;

2) замкнутые и открытые шары;

3) гиперплоскости;

4) замкнутые и открытые полупространства;

5) замкнутые и открытые параллелепипеды;

6) положительный и неотрицательный октанты.

3.2. Множества ограниченные, неограниченные.

  Ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольногометрического пространства, а также на случай произвольногочастично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общихтопологических пространствах, безметрики.

Ограниченное числовое множество

Множество вещественных чисел называетсяограниченным сверху, если существует число

Множество вещественных чиселназываетсяограниченным снизу, если существует число

Множество , ограниченное сверху и снизу, называетсяограниченным.

Множество , не являющееся ограниченным, называетсянеограниченным. Как следует из определения, множество не ограничено тогда и только тогда, когда оно не ограничено сверху или не ограничено снизу.

Примеры:

Примером ограниченного множества является отрезок ,

неограниченного — множество всех целых чисел ,

ограниченного сверху, но неограниченного снизу — луч

ограниченного снизу, но неограниченного сверху — луч