
Надежность систем теплоснабжения / Газизов РЗ
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ПТС
Расчетное задание по дисциплине:
«Надежность установок и систем теплоснабжения промышленных предприятий»
Вариант №1.
Выполнил: студент группы ПТС 06
Газизов К.Ш.
Принял: Акутин М.В.
КАЗАНЬ 2010
Структурная
схема надежности приведена на рис 1.1.
Значения интенсивности отказов элементов
даны в
 1/ч.
1/ч.
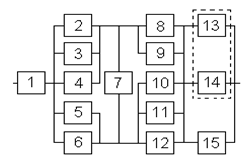
Рис.1.1 исходная схема системы
γ=90%;
λ1=0,1;
λ2=λ3= λ4=λ5= λ6=1;
λ7 =0,5;
λ8= λ9= λ10= λ11= λ12= 1;
λ13= λ14=λ15=0,01.
-
В исходной схеме элементы 2,3 и 4 образуют параллельное соединение. Заменяем их квазиэлементом А, для которых при p2=p3= p4получим:
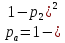
-
элементы 5 и 6 образуют параллельное соединение. Заменяем элементом B, для которой p5=p6 :

-
элементы 8 и 9 образуют параллельное соединение. Заменим элементом С, для которого p8=p9 :
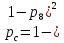
-
элементы 10,11 и 12 образуют параллельное соединение. Заменим элементом D, для которого p10=p11 =p12
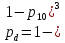
-
элементы
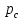 и
и
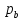 образуют параллельное соединение.
Заменим элементом E,
для которого pc=pb
:
образуют параллельное соединение.
Заменим элементом E,
для которого pc=pb
:

-
элементы
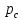 и
и
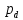 образуют параллельное соединение.
Заменим элементом G,
для которого pc=pd
:
образуют параллельное соединение.
Заменим элементом G,
для которого pc=pd
:
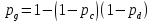
-
элементы A,B,C и D образуют параллельное соединение. Заменим элементом O
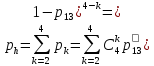

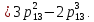
-
В преобразованной схеме элементы 1,H,O и 15 образуют последовательную соединение. Тогда вероятность безотказной работы всей системы составит:
 .
.
10. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 1.1) подчиняются экспоненциальному закону:
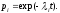
11. Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле для наработки до 3x106 часов представлены в таблице 1.1.
12. Результаты расчетов вероятностей безотказной работы квазиэлементов A, B, C, D, E, G,H. также представлены в таблице 1.1.
13. На рис. 1.5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.
14. По графику находим для γ=90 - процентную наработку системы T=0.4x106.
15. Проверочный расчет при t=0.4x106 ч показывает , что Py=0.54.
16. По условиям задания повышенная γ – процентная наработка системы будет равна 0.9x106 ч.
17.
Расчет
показывает (таблица 1.1), что при 0.9x106
ч для элементов преобразованной схемы
Следовательно, из трех последовательно
соединенных элементов минимальное
значение вероятности безотказной работы
имеет элемент
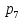 именно увеличение его надежности даст
максимальное увеличение надежности
системы в целом .
именно увеличение его надежности даст
максимальное увеличение надежности
системы в целом .
19.
Для
того, чтобы при
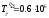 ч система в целом имела вероятность
безотказной работы
ч система в целом имела вероятность
безотказной работы
 ,
необходимо, чтобы элемент 7 имел
вероятность безотказной работы
,
необходимо, чтобы элемент 7 имел
вероятность безотказной работы
 (7.11)
(7.11)
При этом значении элемент O останется самым ненадежным в схеме) и рассуждения в п.18 останутся верными.
Очевидно,
значение
 ,
полученное по формуле (7.11), является
мини-мальным для выполнения условия
увеличения наработки не менее, чем в
1.5
раза,
при более высоких значениях
,
полученное по формуле (7.11), является
мини-мальным для выполнения условия
увеличения наработки не менее, чем в
1.5
раза,
при более высоких значениях
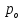 увеличение надежности системы будет
большим.
увеличение надежности системы будет
большим.
20.
Для определения минимально необходимой
вероятности безотказной работы элементов
7 (рис. 7.1) необходимо решить уравнение
относительно
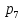 .
Однако, т.к. аналитическое выражение
этого уравнения связано с определенными
трудностями , более целесообразно
использовать графо-аналитический метод.
Для этого по данным табл. 7.1 строим график
зависимости
.
Однако, т.к. аналитическое выражение
этого уравнения связано с определенными
трудностями , более целесообразно
использовать графо-аналитический метод.
Для этого по данным табл. 7.1 строим график
зависимости
 .
График представлен на рис.
.
График представлен на рис.

Рис. Зависимость вероятности безотказной работы системы O от вероятности безотказной работы ее элементов.
21.
По графику при
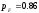 находим
находим
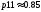 .
.
22.
Так как по условиям задания все элементы
работают в периоде нормальной эксплуатации
и подчиняются экспоненциальному закону
то для элементов 7 при
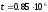 находим
находим
 ч
ч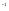 . (7.12)
. (7.12)
23.
Таким образом, для увеличения
 - процентной наработки системы необходимо
увеличить надежность элементов 7 и
снизить интенсивность их отказов с 0.5
до 0,16 т.е. в 2.9 раза.
- процентной наработки системы необходимо
увеличить надежность элементов 7 и
снизить интенсивность их отказов с 0.5
до 0,16 т.е. в 2.9 раза.
24. Результаты расчетов для системы с увеличенной надежностью элементов 7 приведены в таблице 7.1.
Вывод: был произведен расчет структурной схемы надежности системы, построен график изменение вероятности безотказной работы исходной системы.
