Лабораторная работа № 3 Обработка статистических данных на основе приложения ms excel

Задание

Для случайной выборки объемом n=50 с несовпадающими числами выполнить следующую последовательность действий:

1.Вывести на лист Excel исходные статистические данные.

2. Построить вариационный ряд.

3. Вычислить статистические характеристики.

4. Построить интервальный статистический ряд.

5.Построить гистограмму частот.

6. Составить статистическую функцию распределения статистического ряда.

7. Составить и постоить статистическую функцию распределения группированного статистического ряда.

В качестве примера рассмотрим следующую выборку

Порядок выполнения работы

1.Ввод исходных статистических данных.

Вводим данные в первый столбец таблицы (рис.1).

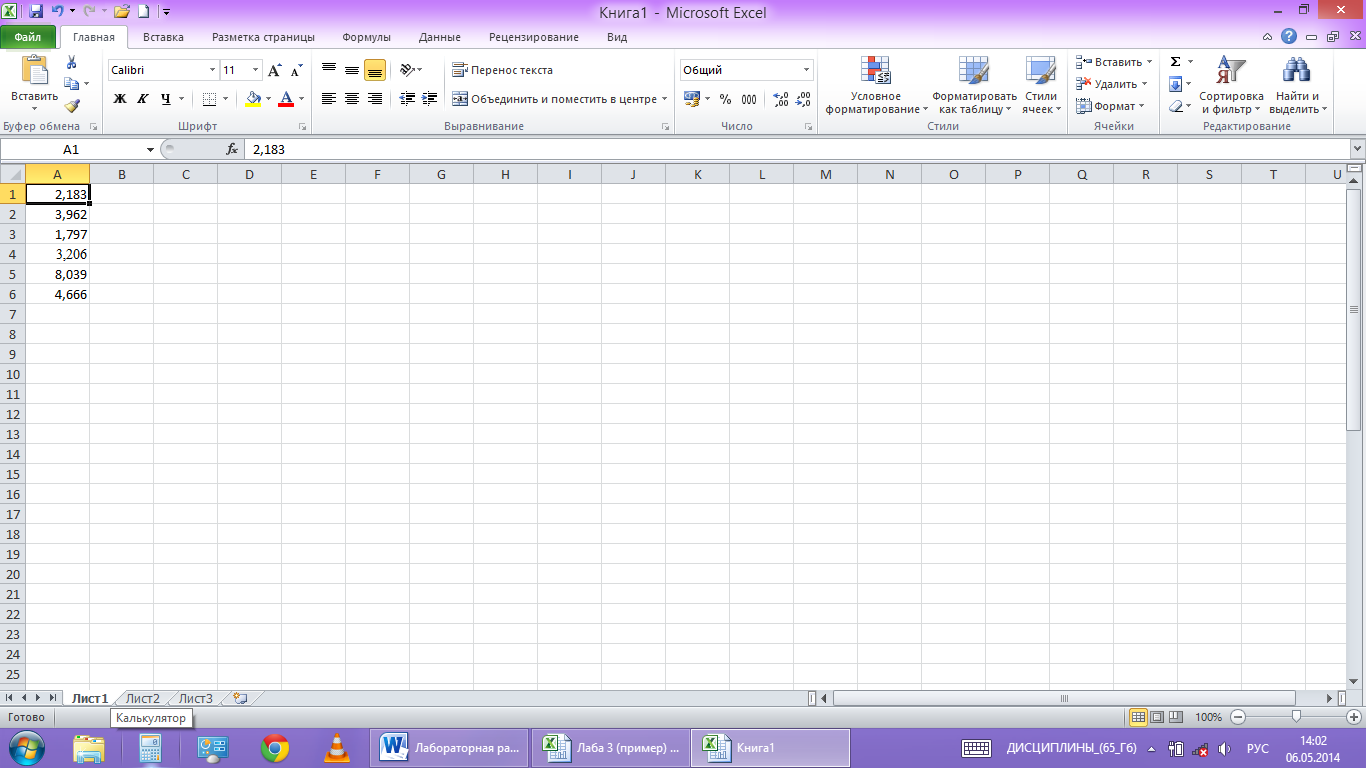
рис.1

2. Построение вариационного ряда.

Производим сортировку данных в порядке возрастания. Для этого:

а) выделяем первый столбец;

б) на ленте во вкладке «Данные» выбираем «Сортировка и фильтр» (рис.2)

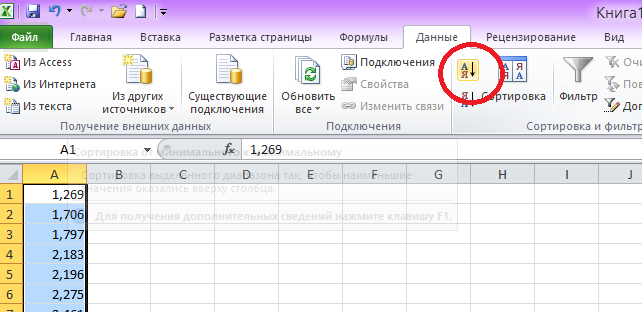
рис. 2

3. Вычисление статистических характеристик.

На ленте во вкладке «Данные» выбираем «Анализ данных» меню «Описательная статистика» нажимаем ОК.

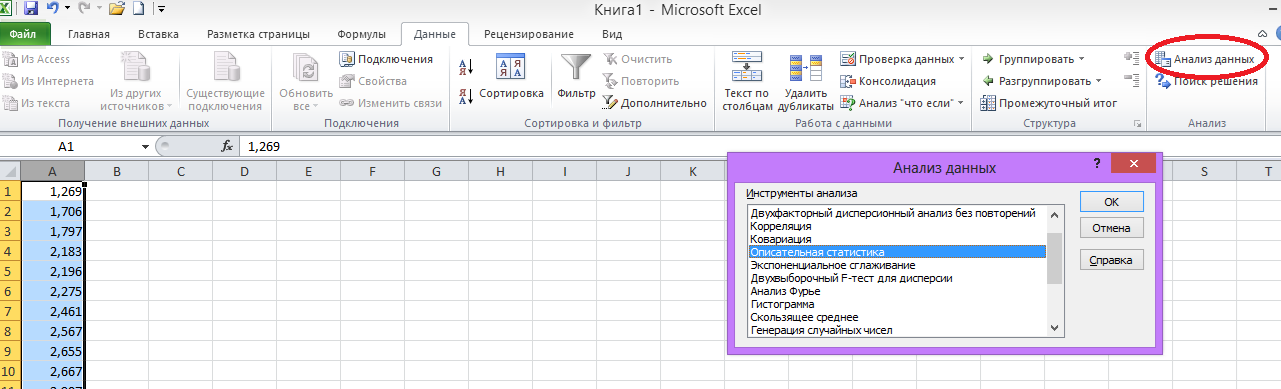
рис. 3

В пункт «Входной интервал» вводим диапазон ячеек с исходными данными $A$1:$A$50, а в пункте «Выходной интервал» обозначим первую ячейку для записи результаов $C$1. Ставим флажок напротив пункта «Итоговая статистика» и нажимаем ОК.(рис.4)

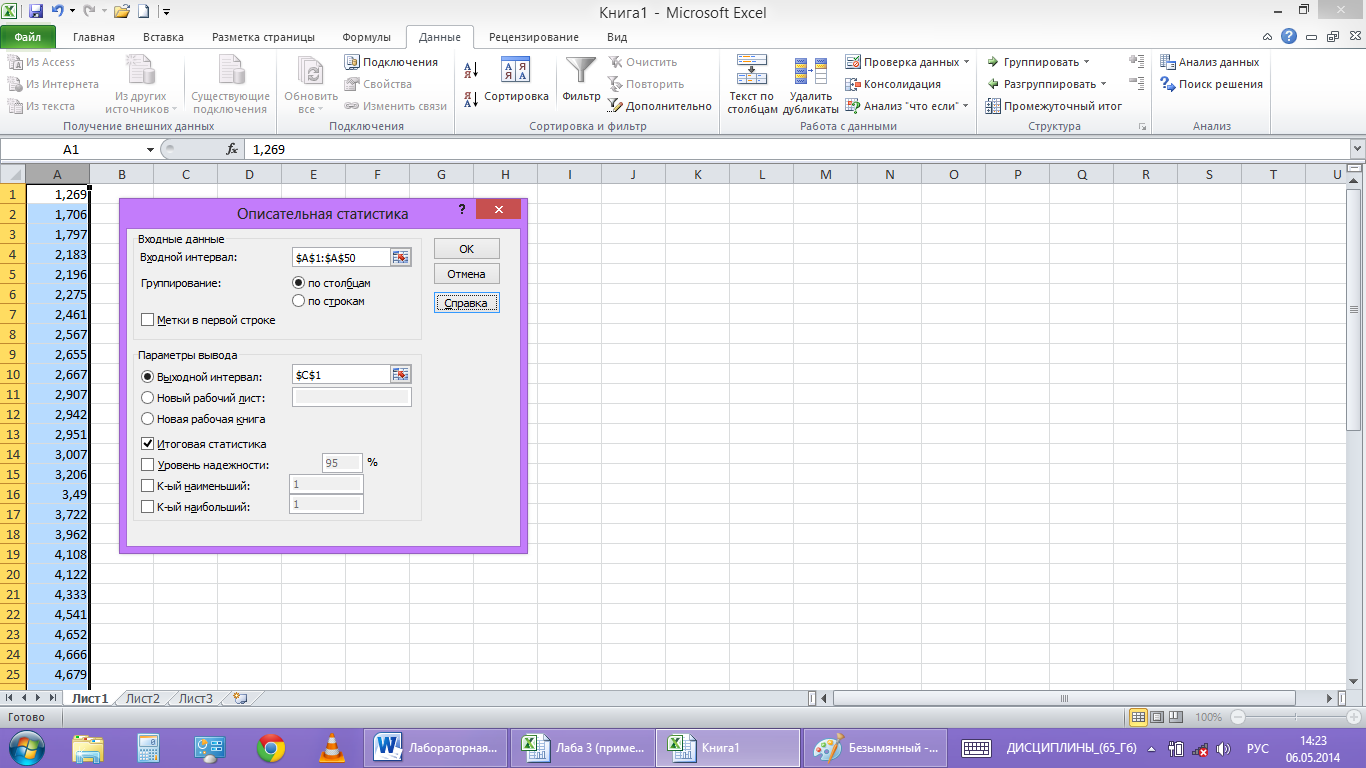
рис. 4

На рабочем листе появляется таблица с вычисленными значениями числовых характеристик выборки (рис.5)

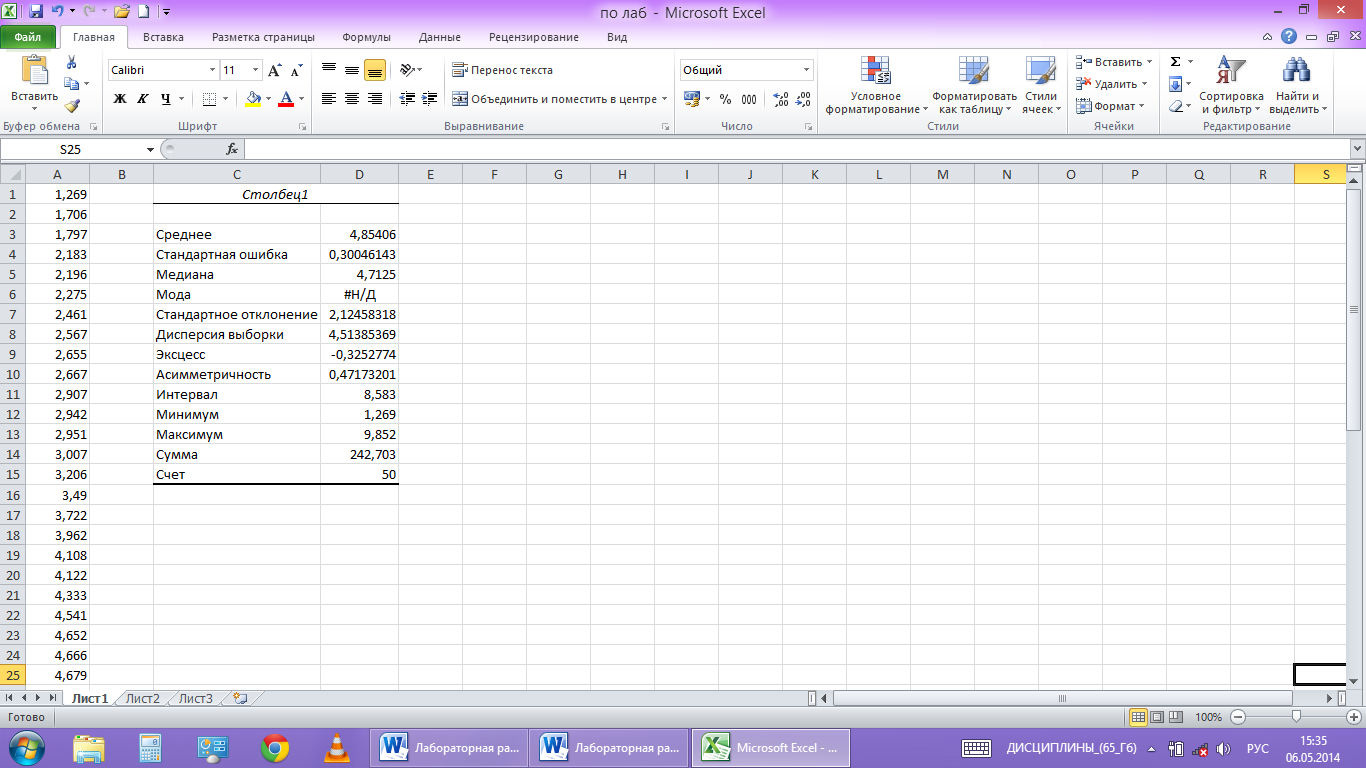
рис. 5

Здесь «Среднее»означает математическое ожидание выборки, а «Стандартная ошибка» - погрешность ее значения. «Дисперсия выборки» означает исправленную выборочную дисперсию, а «Стандартное отклонение» - исправленное среднее квадратичное отклонение. Положительное значение «Асимметричности» означает, что «длинная часть» кривой лежит правее моды. Отрицательное значение «Эксцесса» означает, что кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. «Интервал» равен разности Xmax−Xmin. «Сумма» дает результат суммирования всех элементов выборки. «Счет» задает общее число элементов выборки.

4. Построение интервального статистического ряда.

Длину интервала группировки определяем по формуле

Необходимые данные имеем в таблице: Xmax – в ячейке D13, Xmin– в ячейке D12, число элементов выборки n - в ячейке D15.

В ячейку С16 вводим слово «Интервал», в ячейку D16 вводим формулу

в ячейке D16 появится значение числа h. В ячейку C17 вводим букву h. В ячейку D17 вводим формулу

В ячейке D17 получаем округленное до одного знака после запятой значение интерала h.

Проведем формирование интервалов. Для этого от Xmin отступим влево примерно на h/2 и получим начальную точку отсчета. Последовательно прибавляя к ней целое число отрезков h, получим все граничные точки интервалов.

В ячейку F1 вводим формулу

В этой ячейке появляется значение начальной точки отсчета. В ячейку F2 вводим формулу

В этой ячейке появляется значение второй граничной точки первого интервала. Возвращаемся в ячейку F2, ставим курсор в правый нижний угол рамки и двигаем его вниз, не отпуская левую кнопку мыши. В результате такой процедуры (протяжка) столбец F заполнят граничные точки интервалов. Самый нижний интервал должен включать Xmax (рис.6).

Проведем подсчет числа вариант, попавших в каждый интервал, определим относительные частоты и серединные точки этих интервалов.

Для этого на ленте во вкладке «Данные» выбираем «Анализ данных» меню «Гистограмма». (рис. 7)

рис. 6	рис. 7

В пункт «Входной интервал» вводим диапазон ячеек с исходными данными $A$1:$A$50, в пункт «Интервал карманов» - диапазон ячеек с границами интервалов $F$1:$F$9. Отметим точкой пункт «Выходной интервал» и введем в него адрес первой ячейки для записи результатов $Н$1. Появится таблица из двух столбцов с обозначениями «Карман» и «Частота» (рис.8).

Определим относительные частоты р_i^*, значения серединных точек интервалов

и высоты прямоугольников

Для этого

1. в ячейку J1 введем заголовок «Относительная частота»;

2. В ячейку J3 введем формулу

и протягиваем её вниз до ячейки J10. В результате к таблице из двух столбцов добавится третий столбец (рис.8). В этой таблице частота появления случайной величины в каждом интервале записана в одной строке с концом интервала;

3. в ячейку K1 введем заголовок столбца Х*;

4. в ячейку К3 введем формулу

Протягиваем эту формулу до ячейки К10. В результате в четвертом столбце таблицы (рис.8) появятся значения серединных точек интервалов;

5. в ячейку L1 введем заголовок столбца У_i;

6. в ячейку L3 введем формулу

Протягиваем её вниз до ячейки L10.

В результате в пятом столбце таблицы (рис.8) появятся значения У_i.

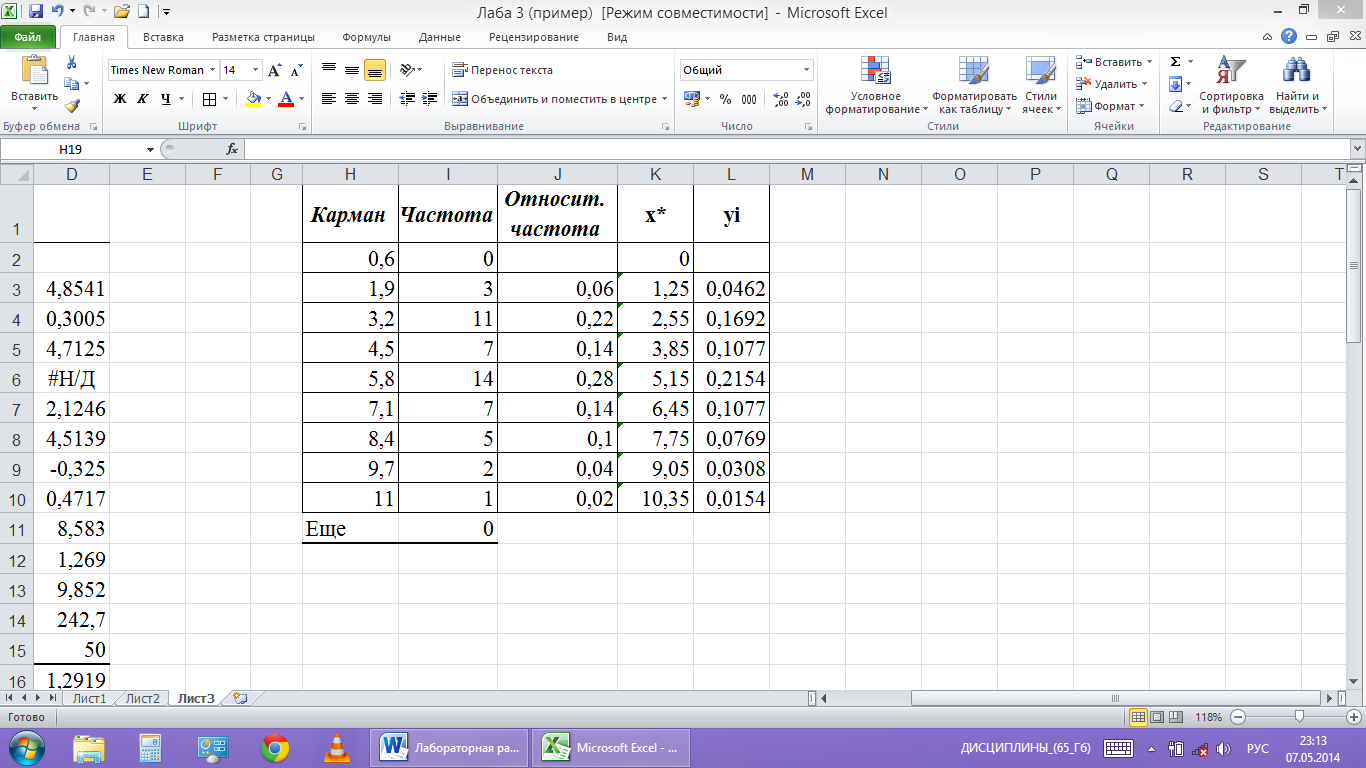
рис.8