Пособие по мат. стат

11

Рис. 1.4

4. Построить гистограмму частот по данному распределению выборки:

12

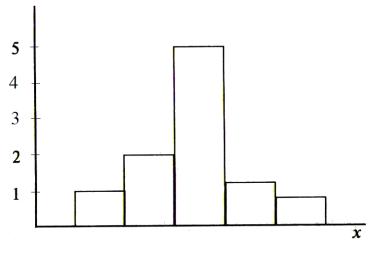
Отложим на оси абсцисс интервалы длиной h 5 каждый, а затем проведем над ними отрезки, параллельные оси x , на расстояниях от нее, равных соответствующим значениям плотности частоты (ось ординат), то есть гистограмма частот состоит из прямоугольников, ширина каждого прямоугольника равна длине интервала h 5 , а высота равна плотности соответствующей частоты (см. рис. 1.5).

Рис. 1.5

5. Построить гистограмму относительных частот и график накопленных частот по данному распределению выборки:

Решение. Найдем относительные частоты и плотности относительных частот:

13

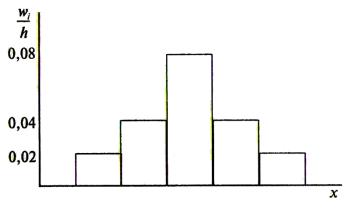
Построим на оси абсцисс частичные интервалы h 5 , затем проведем параллельно им отрезки, отстоящие от оси x на соответствующие значения плотности относительной частоты (см. рис. 1.6).

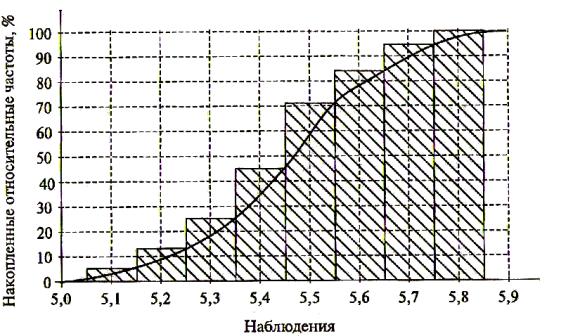
График накопленных частот строится аналогично гистограмме относительных частот, но вместо значений плотностей относительных частот на оси ординат откладываются значения накопленных частот. То есть мы строим прямоугольники, ширина которых равна h 5 , а высоты прямоугольников равны накопленным частотам. Так как накопленные частоты возрастают с увеличением индекса, то и фигура должна получиться возрастающей.

Рис. 1.6

6. Построить эмпирическую функцию по данному распределению выборки:

14

Решение. Найдем объем выборки n : 75 20 5 100. Наименьшая варианта равна 2, следовательно,

Fn (x) 0 при x 2 .

Значение X 3, а именно x1 2 имеет частоту 75, т.е. это значение наблюдалось 75 раз. Следовательно,

Fn (x) 10075 0,75 при 2 x 3 .

Значения X 5, а именно x1 2 и x2 3 наблюдались 75 20 95 раз. Следовательно,

Fn (x) 10095 0,95 при 3 x 5.

Так как x 5 наибольшая варианта, то

Fn (x) 1 при x 5 .

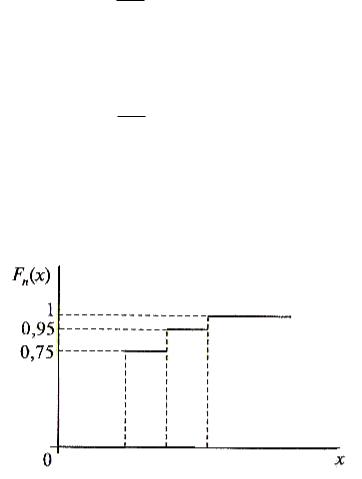
Рис. 1.7

Эмпирическая функция распределения имеет вид (рис. 1.7):

15

7. Анализируется выборка из 100 малых предприятий региона. Цель обследования – измерение коэффициента соотношения заемных и собственных средств (xi ) на каждом i -ом предприятии. Результаты анализа

представлены ниже. Требуется построить гистограмму и график

Решение. 1) Определим по выборке xmin 5,05 и xmax 5,85.

Построим сгруппированный ряд наблюдений (табл. 1.1).

16

Таблица 1.1

Сгруппированный ряд наблюдений

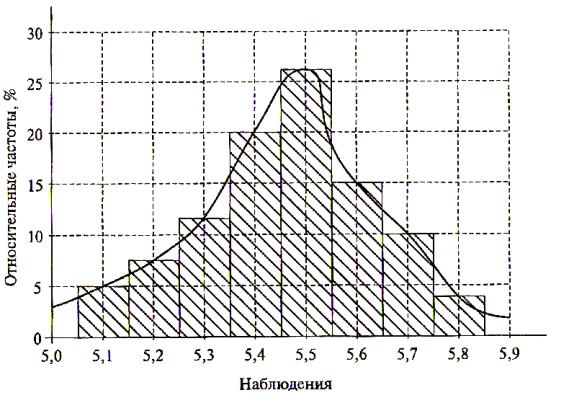
Гистограмма и график накопленных частот представлены на рис. 1.8 и

1.9.

Рис. 1.8

17

Рис. 1.9

8. Путем опроса получены следующие данные (n 80) :

а) Составить статистическое распределение выборки, предварительно записав дискретный вариационный ряд.

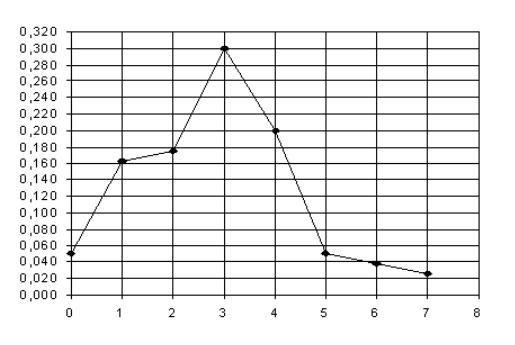
б) Построить полигон частот.

в) Составить ряд распределения относительных частот. г) Составить эмпирическую функцию распределения.

д) Построить график эмпирической функции распределения.

Решение. а) Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания:

Примечание. Указанную процедуру, как и большинство расчетов по математической статистике, удобно выполнять, используя электронные таблицы, например, Microsoft Excel.

Более компактно эти данные можно представить в виде статистического распределения выборки (в виде таблицы, в которой первая

18

строка – варианты (наблюдаемые значения), вторая строка – частоты появления этих вариант):

Изобразим полигон частот вариационного ряда (рис. 1.10).

в) Запишем ряд распределения относительных частот в виде таблицы, в которой первая строка – варианты (изучаемый признак), вторая строка – относительные частоты.

19

Полигон частот вариационного ряда Рис. 1.10

г) Эмпирическую функцию распределения найдем, используя

Таким образом, эмпирическая функция распределения примет вид

20

Задачи для самостоятельного решения

1. Данные выборки приведены в таблице. Построить полигон частот. а)