
1
.docx
 (1.48)
(1.48)
Подобно тому, как коэффициенты массопередачи выражаются через коэффициенты массоотдачи, общее ЧЕП может быть выражено через частное ЧЕП:
 ,
(1.49)
,
(1.49)
для другой фазы:
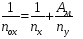 (1.50)
(1.50)
Здесь
 -
фактор процесса массопередачи.
-
фактор процесса массопередачи.
Высота единиц переноса (ВЕП) соответствует высоте участка аппарата, эквивалентного одной единице переноса. ВЕП обычно пропорциональны коэффициентам массоотдачи и массопередачи. Чем больше эти коэффициенты, тем меньше ВЕП и тем меньше высота аппарата, обеспечивающая требуемое разделение веществ.
Общие ВЕП могут быть выражены через частные:
 (1.51)
(1.51)
 (1.52)
(1.52)
ЧЕП можно определить графически или численным интегрированием, ВЕП обычно находят из уравнений, полученных обобщением экспериментальных данных.
29.Упрощенные модели массоотдачи.
Коэффициент массоотдачи характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффициент массоотдачи зависит от многих факторов: физических свойств фазы, скорости потока, определяющих геометрических радиусов и т.д. Определение β требует совместного решения уравнений движения, неразрывности и конвективной диффузии. Это можно сделать для простейшего случая, когда известна поверхность контакта фаз и режим ламинарный. Например, вблизи границы раздела фаз коэффициент массоотдачи для бинарной смеси можно определить по формуле:
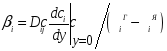
Определение этого коэффициента может быть выполнено экспериментально
Поэтому для определения β иногда пользуются упрощёнными моделями.
Плёночная модель (Нернст, Льюис, Уитмен)
Предполагается,
что вблизи межфазной поверхности
располагается тонкая неподвижная или
ламинарно движущаяся плёнка толщиной
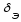 ,
в которой сосредоточено всё сопротивление
массоотдачи. Таким образом, эта плёнка
представляет собой диффузионный
пограничный слой. Предполагается также
постоянство диффузионного потока
поперек слоя. Тогда имеем:
,
в которой сосредоточено всё сопротивление
массоотдачи. Таким образом, эта плёнка
представляет собой диффузионный
пограничный слой. Предполагается также
постоянство диффузионного потока
поперек слоя. Тогда имеем:
 (1.53)
(1.53)
Параметром
модели является
 ,
которая в рамках самой модели не
определяется, что является недостатком
модели. Кроме того,
,
которая в рамках самой модели не
определяется, что является недостатком
модели. Кроме того,
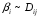 -
(прямая пропорциональность), что не
подтверждается на практике. Данная
модель пригодна лишь для качественного
анализа.
-
(прямая пропорциональность), что не
подтверждается на практике. Данная
модель пригодна лишь для качественного
анализа.
Модель турбулентного диффузионного пограничного слоя
Ландау – Левича
Модель
применима для больших значений
диффузионного критерия Прандтля
 ,
т.е. для жидкостей.
,
т.е. для жидкостей.

Рис.1.8. Схема турбулентного диффузионного пограничного слоя
Предполагается,
что в ядре потока концентрация вещества
постоянна, в пределах
 (турбулентный погранслой) концентрация
снижается, в вязком подслое
(турбулентный погранслой) концентрация
снижается, в вязком подслое
 концентрация уменьшается очень быстро,
в пределах диффузионного подслоя
концентрация уменьшается очень быстро,
в пределах диффузионного подслоя
 молекулярный перенос становится
основным.
молекулярный перенос становится
основным.
Для систем жидкость – твёрдое тело m=3, для систем г-ж, ж-ж m=2.
Получено
для m=3:
 ,
,
m=2:
 ,
(1.54)
,
(1.54)
где

Модель обычно используется для описания массоотдачи в жидкой фазе.
Модель обновления (Хигби).
Предполагается нестационарный молекулярный массоперенос в слой неограниченной толщины, неподвижный относительно границы раздела фаз.
Модель обновления поверхности фазового контакта часто называют моделью проницания. По модели предполагается, что турбулентные пульсации постоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени t, после чего данный элемент обновляется. Предполагается, что t=const для всех элементов поверхности. Формула Хигби:
 (1.55)
(1.55)
Кишиневский,
как и Хигби принимает время контакта
t=const,
но учитывает ещё турбулентные пульсации.
Тогда в формуле (1.55) вместо D
надо принимать (D+Dт).
Модель проницания можно использовать
для массоотдачи в слой ограниченной
толщины, если толщина слоя намного
больше

Недостаток модели: трудность определения t. Так, в насадочном аппарате при стекании жидкой пленки с одного насадка на другой можно допустить ее полное перемешивание .В этом случае в качестве времени контакта t можно использовать время стекания пленки по отдельному элементу насадки.
30. Классификация и основы расчета массообменных аппаратов.
Массообменные аппараты могут подразделяться по различным признакам:
по способу организации процесса:
— периодические,
— непрерывные;
по расположению в пространстве:
— вертикальные,
— горизонтальные,
— наклонные;
по давлению в аппарате:
— атмосферное,
— под избыточным давлением,
— под вакуумом;
по назначению: абсорберы, перегонные аппараты, ректификационные колонны, экстракторы, адсорберы, сушилки, кристаллизаторы и т.д.;
по способу организации контакта фаз:
— с непрерывным контактом фаз (плёночные, насадочные),
— со ступенчатым контактом фаз (тарельчатые);
по конструкции (будет рассматриваться при изучении конкретных типовых процессов).
Технологический расчет аппарата с непрерывным контактом фаз
Большинство массообменных процессов проводят в цилиндрических вертикальных аппаратах (колоннах) непрерывного действия. Технологический расчёт заключается в определении основных размеров аппарата, для колонны это диаметр D и высота Н.
Исходными данными при проектном расчёте являются:
-
расход одной из фаз
 ,
начальная и конечная концентрация
распределяемого компонента в ней
,
начальная и конечная концентрация
распределяемого компонента в ней
 и
и
 .
.
-
начальная концентрация распределяемого
компонента в другой фазе
 .
.
Определяются в ходе расчёта:
-
конечная концентрация
 и расход второй фазы
и расход второй фазы
 .
.
Расчёт ведётся по основному уравнению массопередачи:
 (1.56)
(1.56)
Согласно
этому уравнению, для нахождения F
необходимо найти количество распределяемого
компонента, переходящего из одной фазы
в другую за единицу времени
 ,
среднюю движущую силу
,
среднюю движущую силу
 и коэффициент массопередачи
и коэффициент массопередачи
 .
.
Определение
 и
и
 .
.
Запишем уравнение материального баланса для распределяемого вещества для аппарата в целом:
 (1.57)
(1.57)
По
известным
 ,
,
 ,
,
 находим
находим
 .
По уравнению
.
По уравнению
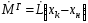 найти
найти
 и
и
 невозможно.
невозможно.
Задаваясь
произвольным значением
 можно найти
можно найти
 ,
однако на
,
однако на
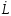 существует ограничение, связанное с
направлением процесса массопередачи.
Допустим, надо организовывать процесс
переноса распределяемого компонента
из фазы у в фазу х. Условие его проведения
у > y*
= mx
(рис.1.9).
существует ограничение, связанное с
направлением процесса массопередачи.
Допустим, надо организовывать процесс
переноса распределяемого компонента
из фазы у в фазу х. Условие его проведения
у > y*
= mx
(рис.1.9).

Рис.1.9.Располажение рабочей и равновесной линий (противоток)
Точка
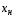 ,
, соответствует верхнему сечению аппарата.
Из точки
соответствует верхнему сечению аппарата.
Из точки
 ,
,
 проводим серии рабочих линий, до касания
равновесной, для точки касания движущая
сила равна нулю и
проводим серии рабочих линий, до касания
равновесной, для точки касания движущая
сила равна нулю и
 =
= min,
min, :
:

Надо,
чтобы
 >
>
 min.
min.
 можно найти решив задачу оптимизации.
Для начала можно брать
можно найти решив задачу оптимизации.
Для начала можно брать
 .
Для этого случая
.
Для этого случая
 находим из (1.57)
находим из (1.57)
 ,
а затем среднюю движущую силу
,
а затем среднюю движущую силу ;
;
 ,
,
 - движущая сила массопередачи в верхнем
и нижнем сечениях аппарата.
- движущая сила массопередачи в верхнем
и нижнем сечениях аппарата.

Определение
скорости движения фаз и диаметра аппарата
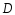 .
.
Расчётные формулы:
 (1.58)
(1.58)
Здесь
 ,
,
 - объёмные расходы фаз;
- объёмные расходы фаз;
 ,
,
 -
первоначальные фиктивные скорости фаз,
отнесенные ко всей поперечной площади
аппарата
-
первоначальные фиктивные скорости фаз,
отнесенные ко всей поперечной площади
аппарата
 .
По D
подбираем по каталогу колонных аппаратов
.
По D
подбираем по каталогу колонных аппаратов
 и далее уточняют фиктивные скорости.
Реальные фиктивные скорости отличаются
от первоначальных. Для первоначального
подбора
и далее уточняют фиктивные скорости.
Реальные фиктивные скорости отличаются
от первоначальных. Для первоначального
подбора
 и
и
 обычно пользуются эмпирическими
зависимостями.
обычно пользуются эмпирическими
зависимостями.
От скорости движения фаз зависят гидродинамический режим работы аппарата, коэффициенты массопередачи, величина поверхности контакта фаз.
Расчёт
коэффициента массопередачи

Вначале
находят коэффициент массоотдачи каждой
из фаз, пользуясь критериальным уравнениям
для
 .
При выборе критериальных зависимостей
необходимо отдать предпочтение
уравнениям, полученным путем решения
дифференциальных уравнений. Эмпирические
зависимости, обычно, имеют границы
применения.
.
При выборе критериальных зависимостей
необходимо отдать предпочтение
уравнениям, полученным путем решения
дифференциальных уравнений. Эмпирические
зависимости, обычно, имеют границы
применения.
Определение требуемой межфазной поверхности F
По основному уравнению массопередачи определяется требуемая межфазная поверхность:

Нахождение высоты аппарата Н
Используя
величину удельной поверхности контакта
фаз

 вначале можно определить рабочий объем
аппарата:
вначале можно определить рабочий объем
аппарата:

а затем его высоту:
 (1.59)
(1.59)
Проблема
состоит в определении
 .
.
При плёночном течении жидкости по стенкам цилиндрического аппарата и контакте её с газовым потоком имеем:
 (1.60)
(1.60)
Для
насадочного аппарата величину
 можно выразить через удельную поверхность
насадки
можно выразить через удельную поверхность
насадки
 и долю активной поверхности
и долю активной поверхности
 :
:
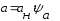 (1.61)
(1.61)
Величина
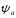 может быть и больше единицы за счёт
образования волн на поверхности плёнки
и брызг жидкости при высоких скоростях
газового потока.
может быть и больше единицы за счёт
образования волн на поверхности плёнки
и брызг жидкости при высоких скоростях
газового потока.
Таким образом, проектный расчёт аппарата с непрерывным контактом фаз в первом приближении завершён, D и Н найдены. Остаётся вопрос, оптимальны ли размеры аппарата?
Критерием
оптимальности могут служить затраты
на проведение процесса. При заданных
характеристиках первой фазы ( ,
, ,
, ),
затраты на проведение абсорбции и
экстракции можно представить в виде
трёх слагаемых V,
Δp,
),
затраты на проведение абсорбции и
экстракции можно представить в виде
трёх слагаемых V,
Δp,
 .
.
В
качестве первого параметра оптимизации
берём расход второй фазы
 :
рост
:
рост
 приводит к росту
приводит к росту
 и Ку и к уменьшению V.
Однако растёт Δр на прокачку фазы
и Ку и к уменьшению V.
Однако растёт Δр на прокачку фазы
 .
.
В
качестве второго параметра оптимизации
возьмём фиктивную скорость
 .
При увеличении
.
При увеличении
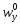 уменьшается D,
возрастает
уменьшается D,
возрастает
 и
и
 ,
что приводит к уменьшению V,
но растёт Δр аппарата.
,
что приводит к уменьшению V,
но растёт Δр аппарата.
Варьирование значениями параметров оптимизации позволяет спроектировать аппарат, обеспечивающий минимальные затраты на проведение процесса.
31. Технологический расчет аппарата со ступенчатым контактом фаз.
Особенность процесса – существенная дискретная неоднородность удельной поверхности контакта фаз по высоте аппарата. Кроме того, в большинстве случаев для них не приемлемо допущение о параллельном движении фаз в режиме идеального вытеснения, которое использовалось при выводе основного уравнения массопередачи.
Рассмотрим схему проектного технологического расчёта массообменного аппарата со ступенчатым контактом фаз на примере тарельчатой колонны с противоточным движением газовой и жидкой фаз (рис.1.10).
Расход
жидкой фазы
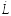 ,
его конечная концентрация, диаметр
аппарата
,
его конечная концентрация, диаметр
аппарата
 и
скорости движения фаз
и
скорости движения фаз
 и
и
 определяется также, как и для аппарата
с непрерывным контактом фаз.
определяется также, как и для аппарата
с непрерывным контактом фаз.

Рис. 1.10. Изменение концентраций фаз по высоте тарельчатой колонны (а) и схема тарельки (б)
Высоту
колонны можно связать с числом тарелок
N
и межтарельчатым расстоянием
 :
:
 (1.62)
(1.62)
Величина
 ,
являясь одним из параметров оптимизации,
в первом приближении может определяться
из условия максимально допустимого
уноса капель газовым потоком. Для
различных типов тарелок имеются
соотношения связывающие величину уноса
е с
,
являясь одним из параметров оптимизации,
в первом приближении может определяться
из условия максимально допустимого
уноса капель газовым потоком. Для
различных типов тарелок имеются
соотношения связывающие величину уноса
е с
 и скоростью газовой фазы
и скоростью газовой фазы
 .Обычно
допускают 0,1
кг жидкости
на 1 кг газа.
.Обычно
допускают 0,1
кг жидкости
на 1 кг газа.
Основная
задача – определение N,
обеспечивающих необходимый перенос
распределяемого компонента из одной
фазы в другую. Для этого вводится понятие
эффективности тарелки по Мэрфри (кпд
тарелки)
 ,
характеризующее степень достижения
равновесия между уходящими с тарелки
фазами:
,
характеризующее степень достижения
равновесия между уходящими с тарелки
фазами:
 (1.63)
(1.63)
где
 -
концентрация распределяемого компонента
в газовой фазе, равновесная с уходящим
с l-ой
тарелки потоком жидкости. Аналогичным
образом можно найти
-
концентрация распределяемого компонента
в газовой фазе, равновесная с уходящим
с l-ой
тарелки потоком жидкости. Аналогичным
образом можно найти
 ,
используя концентрации жидкой фазы.
,
используя концентрации жидкой фазы.
Если
 ,
то такую тарелку называют теоретической.
Т.е. имеем такой объём аппарата,
концентрация распределяемого вещества
на выходе из которого
,
то такую тарелку называют теоретической.
Т.е. имеем такой объём аппарата,
концентрация распределяемого вещества
на выходе из которого
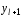 равна равновесной концентрации на входе
в него:
равна равновесной концентрации на входе
в него:
 .
В этом объёме аппарата происходит
процесс полного (теоретического) обмена
распределяемого вещества между обеими
фазами.
.
В этом объёме аппарата происходит
процесс полного (теоретического) обмена
распределяемого вещества между обеими
фазами.
Следует
отметить, что при этом составы фаз
рассматриваются в различных сечениях
аппарата ( -
над l-ой
тарелкой,
-
над l-ой
тарелкой,
 -
под ней). Таким образом, в любом поперечном
сечении аппарата равновесие не достигается
-
под ней). Таким образом, в любом поперечном
сечении аппарата равновесие не достигается
 ,
иначе отсутствовала бы движущая сила
массопередачи.
,
иначе отсутствовала бы движущая сила
массопередачи.
Рассмотрим различные способы определения число тарелок N.
Потарелочный расчёт колонны.
Это аналитический метод определения N основан на решение уравнений материального баланса, равновесия и использования эффективности по Мэрфи для каждой тарелки.
Для
нижней тарелки под номером 1составы фаз
известны
 .
.
Рассмотрим вторую тарелку. Запишем необходимые уравнения:
уравнение
равновесия
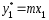 ,
(1.64)
,
(1.64)
уравнение
Мэрфри
 ,
(1.65)
,
(1.65)
уравнение
рабочей линии
 ,
(1.66)
,
(1.66)
Итак нашли составы фаз для тарелки 2. Далее, также для 3 тарелки и т.д.
Для
тарелки
 имеем:
имеем:
 (1.67)
(1.67)
 (1.68)
(1.68)
 (1.69)
(1.69)
Расчёт
заканчивается при значении l,
для которого
начинает выполняться условие
 ,
при этом число тарелок N=l.
Поскольку число тарелок в аппарате
может достигать сотни и более, данный
алгоритм необходимо реализовать на
компьютере.
,
при этом число тарелок N=l.
Поскольку число тарелок в аппарате
может достигать сотни и более, данный
алгоритм необходимо реализовать на
компьютере.
Для ориентировочных расчётов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.
Определение числа тарелок с помощью кинетической кривой.
Эффективность по Мэрфри рассчитывается не для каждой тарелки, а лишь для нескольких сечений колонны, аналитическое решение уравнений (1.64-1.69) заменяется графическим.
Алгоритм действий следующий:
— строятся рабочая и равновесная линии;
— для
нескольких сечений аппарата (нескольких
рабочих концентраций ;
;
 ;
;
 )
рассчитываются эффективности по Мерфри
)
рассчитываются эффективности по Мерфри

—находят
величины.
 (1.70)
(1.70)
— на
диаграмме х – у наносятся точки
 и т.д. Соединяя их получим кинетическую
кривую.
и т.д. Соединяя их получим кинетическую
кривую.
— из
точки
 спускаемся по лестнице до тех пор, пока
для точки
спускаемся по лестнице до тех пор, пока
для точки
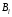 не выполнится
условие
не выполнится
условие
 .
На этом построение заканчивается,
необходимое число тарелок в колонне
.
На этом построение заканчивается,
необходимое число тарелок в колонне
 .
.
Таким образом, аналитическое решение заменяется графическим определением число ступеней лестницы.

Рис.1.11. Определение числа тарелок с помощью кинетической кривой:
1 – рабочая линия, 2 – равновесная линия, 3 – кинетическая кривая.
Определение числа тарелок с помощью кпд колонны
Кпд колонны:
 (1.71)
(1.71)
где
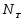 -
теоретическое число тарелок, N
– действительное число тарелок. Величина
-
теоретическое число тарелок, N
– действительное число тарелок. Величина
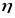 находится
из опыта. Найти
находится
из опыта. Найти
 опытным путём достаточно сложно.
Необходимы данные по идентичной колонне.
опытным путём достаточно сложно.
Необходимы данные по идентичной колонне.
Алгоритм действий следующий:
аналитическим
или графическим способом определяется
 .
.
по
известным эмпирическим формулам
рассчитывается к.п.д. колонны
 .
.
по
формуле (1.71) находят необходимое
 .
.
32. АБСОРБЦИЯ.
Абсорбцией называется процесс избирательного поглощения газов или паров из газовых или парогазовых смесей жидким поглотителем – абсорбентом. Если поглощаемый газ – абсорбтив – химически не взаимодействует с абсорбентом, то такая абсорбция физическая, если же абсорбтив образует с абсорбентом химическое соединение, то такой процесс называется хемосорбцией. Физическая абсорбция обратима, выделение поглощаемого газа из раствора – десорбция. Сочетание абсорбции и десорбции позволяют многократно использовать поглотитель и выделять поглощённый газ в чистом виде. Инертный газ – компонент газовой смеси не переходящий границу раздела фаз.
Абсорбция применяется:
для
получения готового продукта (абсорбция
 в производстве серной кислоты, абсорбция
HCl,
оксидов азота водой в производстве
азотной кислоты);
в производстве серной кислоты, абсорбция
HCl,
оксидов азота водой в производстве
азотной кислоты);
для выделения ценных компонентов из газовых смесей (абсорбция бензола из коксового газа, абсорбция ацетилена из газов крекинга или пиролиза природного газа и т.д.), при этом абсорбцию проводят в сочетании с десорбцией;
для очистки газовых выбросов от вредных примесей;
для осушки газов.
Равновесие при абсорбции. Закон Генри.
Система
состоит из трёх компонентов (распределяемое
вещество А и два распределяющих вещества)
и двух фаз – жидкой и газовой. Такая
система по правилу фаз имеет три степени
свободы:
 .
Для абсорбции переменными являются Т,
Р, концентрация компонента А в газовой
и жидкой фазах. Следовательно, в состоянии
равновесия при Т=const
и постоянном общем давлении Р зависимость
между парциальным давлением газа
.
Для абсорбции переменными являются Т,
Р, концентрация компонента А в газовой
и жидкой фазах. Следовательно, в состоянии
равновесия при Т=const
и постоянном общем давлении Р зависимость
между парциальным давлением газа
 или его концентрацией и составом жидкой
фазы однозначна. Эта зависимость
выражается законом Генри: парциальное
давление
или его концентрацией и составом жидкой
фазы однозначна. Эта зависимость
выражается законом Генри: парциальное
давление
 растворённого газа пропорционально
его мольной доле
растворённого газа пропорционально
его мольной доле
 в растворе:
в растворе:
 (2.1)
(2.1)
где
 - парциальное давление поглощаемого
газа над раствором, находящегося в
равновесии, при концентрации раствора
- парциальное давление поглощаемого
газа над раствором, находящегося в
равновесии, при концентрации раствора
 ,
Е – константа Генри. Е не зависит от
общего давления в системе, но зависит
от природы абсорбента и поглощаемого
газа, а также от Т.
,
Е – константа Генри. Е не зависит от
общего давления в системе, но зависит
от природы абсорбента и поглощаемого
газа, а также от Т.
Растворимость газа в жидкости при данной температуре пропорционально его парциальному давлению над жидкостью:
 (2.2)
(2.2)
Здесь
 -
концентрация газа в растворе, равновесная
с газовой фазой, в которой парциальное
давление поглощаемого компонента равна
-
концентрация газа в растворе, равновесная
с газовой фазой, в которой парциальное
давление поглощаемого компонента равна
 .
.

Рис.2.1 Растворимость газа в жидкость от Т.

Для идеальных растворов на диаграмме р–х (рис.2.1) зависимость равновесных концентраций от давления изображается прямой, с наклоном, равным Е.
Как видно из рис.2.1,чем больше Т, тем меньше растворимость.
Если
 –
молярная доля извлекаемого компонента
А в газовой смеси и Р – общее давление
в системе, то парциальное давление
–
молярная доля извлекаемого компонента
А в газовой смеси и Р – общее давление
в системе, то парциальное давление
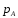 ,
по закону Дальтона, можно записать:
,
по закону Дальтона, можно записать:
 (2.3)
(2.3)
Тогда, с учетом уравнения (2.1) получим:

Итак для закона Генри имеем:
 (2.4)
(2.4)
Здесь
 - коэффициент распределения, или константа
фазового равновесия.
- коэффициент распределения, или константа
фазового равновесия.
Величина m уменьшается с увеличением Р и снижения Т. Таким образом, растворимость газа в жидкости растёт с ростом давления и снижения Т.
Когда в равновесии с жидкостью находятся смесь газов, закону Генри может следовать каждый из компонентов смеси в отдельности.
Закон Генри справедлив только для идеальных газов, а также к сильно разбавленным реальным растворам. Для хорошо растворимых газов, при больших концентрациях их в растворе, растворимость меньше, чем по закону Генри. Для систем, не подчиняющихся закону Генри, m является величиной переменной и линия равновесия представляет собой кривую, которую строят обычно по опытным данным.
При больших давлениях (1 МПа и выше) изменение объёма жидкости вследствие растворения в ней газа соизмеримо с изменением объёма газа и равновесие в этом случае не следует закону Генри. При этих условиях константу фазового равновесия можно определить как:
 (2.5)
(2.5)
 - фугитивность
(летучесть) поглощаемого газа, выраженная
в единицах давления.
- фугитивность
(летучесть) поглощаемого газа, выраженная
в единицах давления.
При записи уравнений материального баланса и рабочих линий целесообразно выбрать единицы измерения расходов таковыми, чтобы эти величины не менялись по высоте аппарата. Это сделает рабочие линии прямыми.
