1

Рис. 3.3. Противоточная многокорпусная выпарная установка

В качестве греющего теплоносителя в выпарных установках используется насыщенный водяной пар с давлением р = 0,5–1,0 МПа и температурой 140–180 С.

Конструкции выпарных аппаратов (ВА) многообразны: с паровой «рубашкой», змеевиковый, с горизонтальной греющей камерой, вертикальной греющей камерой (наиболее распространенные), пленочные, роторные и барботажные ВА (рис. 3.4).

Хорошая циркуляция раствора в аппаратуре способствует интенсификации теплообмена, предотвращает быстрое отложение накипи на стенках кипятильных труб.

ВА с естественной циркуляцией движение раствора вызвано различием плотностей парожидкостной смеси в циркуляционной трубе и кипятильных трубах. В этих аппаратах скорости циркуляции небольшие, поэтому реализуются небольшие значения коэффициентов теплопередачи. Скорость циркуляции раствора в ВА с вынесенной трубой больше, чем в аппаратах центральной циркуляцией. Более высокие скорости циркуляции достигаются в ВА с принудительной циркуляцией (для парожидкостной смеси w = 22,5 м/с), поэтому эти аппараты могут работать и при небольших значениях полезных разностях температур. Пленочные ВА используются для разделения нетермостойких растворов.

В пленочном выпарном аппарате с восходящей пленкой жидкости исходный раствор поступает в трубы снизу и заполняет одну четверть трубы. Происходит кипение раствора, образующийся пар увлекает раствор в виде кольцевой пленки. Кольцевая пленка при кипении испаряется (рис. 3.5). Для снижения температуры кипения растворов процесс, как правило, проводится под вакуумом.

Роторные ВА применяются для выпаривания высоковязких пастообразных продуктов. Барботажные ВА используются для выпаривания агрессивных жидкостей. Барботаж осуществляется дымовыми газами с помощью погружных горелок.

24. Материальный и тепловой балансы однокорпусной выпорной установки.

Процесс однократного выпаривания проводят в одном аппарате в непрерывном режиме (рис. 3.1). Схема массовых и тепловых потоков приведена на рис. 3.6.

Рис. 3.6. Схема массовых и тепловых потоков ВА

Материальный баланс по общему количеству продуктов

. (89)

Здесь  расход исходного и упаренного растворов, ;  выход вторичного пара, .

Материальный баланс по нелетучему продукту

, (90)

где x_н,, x_к  концентрация растворенного продукта в исходном и упаренном растворе на 1 кг продукта.

В этих уравнениях искомые величины:

(91)

По двум исходным уравнениям три величины найти невозможно, поэтому одной из величин, например, задаемся.

Расход теплоты на проведение процесса определяют из уравнения теплового баланса

. (92)

Здесь  расход греющего пара, ;  энтальпия, ;  потери теплоты в окружающую среду, . Индексы н – начальное, к – конечное, вп – вторичный пар, п – потери, г  греющий пар, гк – конденсат греющего пара.

Вводя упрощающие допущения в уравнение (92), приведем его к виду более удобному для пользования. Запишем тепловой баланс смешения, рассматривая исходный раствор как смесь упаренного раствора и испаренной влаги при постоянной температуре кипения, сделав допущение о постоянстве с_н в интервале температур Т_н и Т_к

, (93)

где с_в – удельная теплоемкость воды при температуре Т_к; – теплота концентрирования раствора в интервале изменения концентрации от х_н до х_к. Теплота концентрирования равна теплоте разбавления с обратным знаком

Тогда получим

. (94)

Здесь – количество теплоты, выделяющееся в выпарном аппарате при конденсации пара;  теплота на нагревание исходного сырья от до ;  теплота на испарение растворителя при . При небольшой степени концентрирования и хорошей изоляции выражение мало и им можно пренебречь. Если предположить, что T_н = T_к, т.е. раствор поступает в аппарат при температуре кипения, то

,

отсюда

, (95)

где r_п  теплота парообразования растворителя; r_к  теплота конденсации греющего пара.

Если в качестве греющего пара используют насыщенный водяной пар, а упаривают водный раствор, то . Это означает, что на испарение 1 кг растворителя затрачивается 1 кг греющего пара. Реально, , т.е. пара необходимо больше в 1,051,15 раз. Уравнение (94) используется для определения тепловой нагрузки. Потребная площадь теплопередачи определяется по основной расчетной формуле

.

Здесь искомая величина 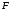, а K  коэффициент теплопередачи определяется по известным формулам. Возникает проблема расчета полезной разности температур .

25.Температурные потери в выпарных установках. Способы распределения полезной разности температур по корпусам.

Обычно в однокорпусных выпарных установках известны давления греющего и вторичного паров, т.е. их температуры. Разность между температурами греющего и вторичного паров называют общей разностью температур выпарных аппаратов

. (96)

Общая разность температур связана с полезной разностью температур соотношением

. (97)

Здесь   концентрационная температурная депрессия;   гидростатическая температурная депрессия.  определяют как разницу температур кипения раствора Т_{кип. р} и чистого растворителя Т_{кип. чр} при p = = const

 = Т_{кип. р} – Т_{кип. чр}, Т_{кип. чр} = T_вп,  = Т_{кип. р}  T_вп. (98)

Температура образующегося при кипении раствора вторичных паров ниже, чем температура кипения самого раствора, т.е. часть температур теряется бесполезно.

 характеризует повышение температуры кипения раствора с увеличением гидростатического давления. Обычно по высоте кипятильных труб определяют среднее давление, и для этого давления определяют среднюю температуру кипения растворителя Т_ср.

Здесь p_a  давление в аппарате; _пж  плотность парожидкостной смеси в кипятильных трубах ; H  высота кипятильных труб.

 = T_ср  T_вп, (99)

где T_ср  температура кипения растворителя при p = p_ср; T_вп  температура вторичного пара при давлении p_а.

Для определения поверхности теплопередачи корпусов необходимо знать полезную разность температур для каждого корпуса. Суммарную полезную разность температур в многокорпусной установке находят из уравнений

; (105)

Т_общ = Т_г1  Т_бк, (106)

где Т_г1  температура греющего пара в первом корпусе; Т_бк  температура вторичного пара, поступающего в барометрическую камеру

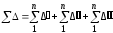. (107)

Здесь '''  гидродинамическая температурная депрессия. Она вызывается потерей давления вторичных паров при переходе из одного корпуса в другой на преодоление гидравлических сопротивлений. Потеря давления насыщенного пара влечет за собой уменьшение его температуры. Величина Δ''' небольшая, обычно ее не рассчитывают, принимают для каждого аппарата ~ 11,5 C.

распределяют между выпарными аппаратами различными способами:

1 способ: поверхности теплообмена по корпусам равны

; (108)

2 способ: суммарная поверхность теплообмена корпусов установки минимальна

. (109)

Рассмотрим 1 способ.

Основное условие первого способа распределения выражается соотношением (108). Полезная разность температур в корпусе

, (110)

тогда суммарная разность температур

. (111)

С учетом (110) получим

; (112)

(113)

Зная значение 1/F из (110) для первого корпуса, получим

. (114)

Аналогично для второго корпуса и т.д.

Таким образом, при равенстве поверхностей теплопередачи в каждом корпусе суммарная полезная разность температур распределяется пропорционально отношению тепловой нагрузки к коэффициенту теплопередачи в каждом корпусе.

Рассмотрим 2 способ.

Запишем уравнение (113) в виде

.

Для нахождения минимума функции F необходимо дифференцировать последнее выражение по , приравнивая полученное частное производное нулю, что является необходимым условием экстремума функции. В результате получено для n-го корпуса

. (115)

При минимальной суммарной поверхности теплоотдачи многокорпусной установки общая полезная разность температур распределяется пропорционально квадрату корня из отношения тепловой нагрузки к коэффициенту теплопередачи в каждом корпусе.

Распределение общей полезной разности температур этим способом приводит к удорожанию изготовления аппаратов и эксплуатации, но дает экономию металла.

26. Массообмен. Фазовые равновесия.

Основная задача химико-технологического процесса состоит в направленном изменении макроскопических свойств участвующих в процессе веществ: состава, агрегатного состояния, давления P и температуры Т. При этом происходит перенос субстанций: массы, энергии, импульса. Предельное состояние системы – подвижное равновесие, при котором не происходит изменений макроскопических свойств веществ. Равновесным называют такое состояние системы, при котором перенос субстанций отсутствует.

В изолированной системе условия равновесия определяется только внутренними условиями и записываются так:

, , (1.1)

Здесь, – химический потенциал -того компонента.

Условия (1.1) называют условиями механического, термического и химического равновесия.

Все самопроизвольные процессы сопровождаются увеличением энтропии системы. В состоянии равновесия энтропия достигает максимального значения:

(1.2)

Таким образом, условия равновесия системы определяются уравнениями (1.1) и (1.2).

Для открытой системы равновесное состояние может быть устойчивым лишь при её равновесии с окружающей средой. Движущая сила процессов переноса возникает вследствие отклонения от равновесия в самой системе или в окружающей среде. Все технологические схемы является открытыми системами.

Химический потенциал зависит не только от концентрации данного компонента, но и от вида и концентрации других компонентов системы.

Химический потенциал компонента непосредственно изменить невозможно. Для его расчета используют соотношения между термодинамическими функциями, которые, в свою очередь, зависят от состава смеси. Поэтому в инженерных расчетах для определения движущей силы процесса используют разность концентраций.

Возможное существование данной фазы в равновесии с другими определяется по закону равновесия фаз Гиббса:

(1.3)

Здесь С – число степеней свободы (Р,Т и концентрация) – минимальное число параметров, которые можно изменять независимо друг от друга, не нарушая равновесие данной системы; – число фаз системы; – число независимых компонентов системы; – число внешних факторов, влияющих на положение равновесия в данной системе.

Для процессов переноса массы =2 ( давление и температура). Правило фаз Гиббса определяет возможность существования фаз, но не указывает на количественных зависимостей переноса вещества между фазами.

Обычно зависимости между параметрами строят в плоских координатах. Такие диаграммы называются фазовыми.

Для бинарной смеси строят следующие фазовые диаграммы: – при Т=const, Т– при =const, y(x)– при T=const, y-x при =const. Здесь - концентрация, y и x – концентрация вещества в фазах.

Рис.1.1. Схема массообменного процесса.

Рассмотрим пример поглощения аммиака чистой водой из аммиачно-воздушной смеси: у - концентрация аммиака в воздухе, х - концентрация аммиака в воде. Аммиак - распределяемый компонент. С началом растворения аммиака в воде начнётся переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде. С течением времени скорость переноса аммиака в воду будет снижаться, а скорость обратного переноса возрастать. Такой двусторонний перенос будет продолжаться до установления динамического равновесия – когда переходы в обоих направлениях будут равны.

При равновесии достигается определённая зависимость между равновесными концентрациями распределяемого вещества в фазах при Т и = const:

, (1.4)

где у* - равновесная концентрация аммиака в воздухе, при концентрации аммиака в воде х.

Графическое изображение зависимости (1.4) и есть линия равновесия. Эту зависимость представим в виде:

у* = mx (1.5)

где m – коэффициент распределения.

Для двухкомпонентной двухфазной системы коэффициент распределения будет зависеть от двух переменных m=f(T,x)=f(,x)=f(,T).

Материальный баланс.

В стационарных условиях закон сохранения массы для всего аппарата в виде материального баланса может быть представлен:

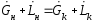(1.6)

, – соответственно, расходы жидкой и газовой фаз; х, у – концентрация распределяемого компонента в фазах; н – начальное, к – конечное состояние.

Материальный баланс по распределённому компоненту при отсутствии химических реакций имеет вид:

(1.7)

В случае постоянства расходов и уравнение (1.7) упрощается:

(1.8)

Для элементарного участка аппарата имеем:

–dy=dx (1.9)

Знак минус свидетельствует о противоположном изменении концентрации распределяемого компонента в фазах, если в одной фазе увеличивается, то в другой – наоборот, уменьшается.

Уравнения рабочих и равновесных линий.

Предположим, что перенос распределяемого компонента происходит из фазы в фазу .

Рис.1.2. Схема массообменного процесса в противоточном аппарате.

Из уравнения материального баланса можно получить уравнение рабочей линии.

Уравнение материального баланса для нижней части аппарата до сечения А-А:

(1.10)

поступает расходуется

Находим из (1.10) у:

В случае постоянства расходов и получим:

(1.11)

Полученное уравнение (1.11) является уравнением рабочей линии и представляет собой уравнение прямой линии.

Аналогичным образом может быть получено уравнение рабочей линии для прямоточного аппарата.

Рис.1.3. Схема массообменного процесса в прямоточном аппарате

(1.12)

поступает расходуется

Находим из (1.12) у: , если расходы не меняются, т.е. и =const, то:

(1.13)

а б

Рис.1.4. Рабочие линии: а – противоток, б – прямоток.

Запишем уравнение равновесной линии, связывающее рабочую концентрацию распределяемого компонента в одной из фаз с его равновесной концентрацией в другой фазе. Под равновесной концентрацией в произвольном сечении аппарата понимают концентрацию компонента в фазе, находящейся в равновесии с другой, состав которой определяется рабочей концентрацией. Уравнение равновесной линии:

у*=mх (1.14)

Здесь у* - равновесная концентрация в фазе G, х – рабочая концентрация в фазе L,

m – коэффициент распределения.

Рис.1.5. Рабочие (1 и 2) и равновесная (3) линии.

Рабочая концентрация распределяемого компонента в фазе G превышает равновесную. Поэтому распределяемый компонент будет переходить из G фазы во вторую фазу L, до равновесия т.к. .

27. Различные модификации уравнений массоотдачи и массопередачи.

Ранее было получено уравнение массопередачи, движущей силой, в которой являлась разница химических потенциалов компонента в ядрах различных фаз. Расчёт химических потенциалов, как известно, задача сложная. Поэтому на практике обычно пользуются уравнениями массотдачи и массопередачи, содержащими в качестве движущей силы разность концентраций компонента.

При использовании интегральной формы уравнений массотдачи и массопередачи большой проблемой является определение поверхности контакта фаз в реальном аппарате, т.к. она может складываться из поверхности струй, капель, пузырей, пены. В этом случае применяют модифицированные уравнения, не содержащие величину межфазной поверхности.

28.Объёмные коэффициенты массоотдачи и массопередачи.

В реальном аппарате определить поверхность контакта фаз, зачастую, бывает сложно, т.к. она может складываться из поверхности струй, пузырей, капель и т.д. Необходимо получить уравнения массотдачи и массопередачи, в которые межфазная поверхность не входит.

Введём понятие удельной поверхности контакта фаз , как поверхность контакта, образующаяся в единичном рабочем объёме аппарата:

(1.37)

Выразив , перепишем уравнения массотдачи и массопередачи:

(1.38)

(1.39)

объёмные коэффициенты массоотдачи и массопередачи. Определить эти коэффициенты теоретическим путём достаточно сложно. Они, обычно, определяются экспериментально. Связь между обычными и объемными коэффициентами массоотдачи и массопередачи имеет следующий вид:

При расчете аппарата со ступенчатым контактом фаз коэффициенты массоотдачи и массопередачи удобнее относить не к объему аппарата, а к площади рабочего сечения контактного устройства , например, площади рабочего сечения тарелки. Вводя удельную поверхность контакта фаз (межфазная поверхность, образующаяся на данном контактном устройстве, отнесенная к его рабочему сечению) можно записать уравнение массопередачи следующим образом:

(1.40)

(1.41)

Аналогичным образом можно переписать и другие уравнения с использованием коэффициентов массоотдачи и массопередачи , отнесенных к площади рабочего сечения контактного устройства:

Число и высота единиц переноса

Для наиболее распространённого типа массообменных аппаратов – цилиндрические вертикальные колонны – основным размером, зависящим от скорости массопередачи, является высота Н.

Если S (площадь поперечного сечения аппарата) постоянная, то его объём можно записать:

(1.42)

Привлекая основное уравнение массопередачи и уравнение материального баланса определим высоту аппарата H:

,

(1.43)

Для процесса массотдачи можно получить Н аналогичным образом:

(1.44)

По другой фазе:

(1.45)

(1.46)

В уравнениях (1.43) – (1.46) первые сомножители называются высотой единицы переноса (ВЕП), а вторые – числом единиц переноса (ЧЕП), причём - называются общими, а 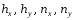- частными или фазовыми.

Тогда по смыслу и - общее ЧЕП – изменение рабочей концентрации распределяемого между фазами компонента, приходящееся на единицу движущей силы. Тогда одна единица переноса соответствует участку аппарата, для которого изменение рабочей концентрации фазы равно средней движущей силе на этом участке.

Общее ЧЕП можно представить по-разному.

(1.47)

Аналогичные соотношения могут быть получены и для частных ЧЕП: