1

Как правило, подобная качественная зависимость выполняется не только для плоского погранслоя, но и для более сложных случаев.

. Турбулентные пограничные слои (рис. 1.4)

Рис. 1.4. Гидродинамический и тепловой турбулентные пограничные слои

на плоской пластине

Задача рассматривается в изотермической постановке, тепловые граничные условия первого рода Т_ст = const.

По мере удаления от кромки пластины (увеличения координаты х) происходит рост _г(х). При этом неоднородность поля скорости w_x распространяется в области все более удаленные от границы раздела фаз, что является предпосылкой возникновения турбулентности. Наконец, при Re_x,кp начинается переход ламинарного режима в турбулентный. Переходная зона соответствует значениям х, рассчитанным по Re_x от 3,5  10⁵ ÷ 5  10⁵. На расстояниях Re_x > 5  10⁵ весь пограничный слой турбулизируется, за исключением вязкого или ламинарного подслоя толщиной _1г. В ядре потока скорость не меняется. Если Pr > 1 то внутри вязкого подслоя можно выделить тепловой подслой толщиной _1т, в котором молекулярный перенос тепла преобладает над турбулентным.

Толщина же всего турбулентного теплового пограничного слоя обычно определяется из условия ν_т = а_т, следовательно _г = _т.

Сначала рассмотрим турбулентный гидродинамический пограничный слой (рис. 1.4). Оставим в силе все приближения, сделанные для ламинарного слоя. Единственное отличие – наличие ν_т (у), поэтому

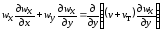. (35)

Сохраним и граничные условия. Решением системы уравнений (35) и (22) с граничными условиями (25), используя полуэмпирическую модель пристенчатой турбулентности Прандтля, можно получить характеристики турбулентного пограничного слоя. В вязком подслое, где реализуется линейный закон распределения скорости, можно пренебречь турбулентным переносом импульса, а вне его молекулярным. В пристенной области (за вычетом вязкого подслоя) обычно принимается логарифмический профиль скорости, а во внешней области – степенной закон с показателем 1/7 (рис. 1.4).

Как и в случае ламинарного пограничного слоя возможно использование осредненных по длине l коэффициентов импульсоотдачи

. (36)

Рассмотрим тепловой турбулентный пограничный слой. Уравнение энергии имеет вид

. (37)

Если Pr > 1, то внутри вязкого подслоя можно выделить тепловой подслой, где молекулярный перенос тепла

. (38)

Для локального коэффициента теплоотдачи решение математической модели имеет вид

. (39)

Среднее по длине пластины значение определяется так

. (40)

Ниже представлены образование турбулентного пограничного слоя (а) и распределение локального коэффициента теплоотдачи (б) при продольном обтекании плоской полубесконечной пластины (рис. 1.5).

Рис. 1.5. Пограничные слои _г и _т и локальный коэффициент теплоотдачи 

на плоской пластине

В ламинарном слое (х ≤ l_кр) тепловой поток реализуется только за счет теплопроводности, для качественной оценки можно использовать соотношение  ~ .

В переходной зоне общая толщина пограничного слоя увеличивается. Однако значение  при этом увеличивается, потому что толщина ламинарного подслоя уменьшается, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией вместе с перемещающейся массой жидкости, т.е. более интенсивно. В результате суммарное термическое сопротивление теплоотдачи убывает. В зоне развитого турбулентного режима коэффициент теплоотдачи вновь начинает убывать из-за возрастания общей толщины пограничного слоя  ~ .

Итак, рассмотрены гидродинамический и тепловой пограничные слои на плоской пластине. Качественный характер полученных зависимостей справедлив и для пограничных слоев, образующихся при обтекании более сложных поверхностей.

14. Теплообмен в круглой трубе

Рассмотрим стационарный теплообмен между стенками горизонтальной прямой трубы круглого сечения и потоком, обладающим неизменными теплофизическими характеристиками и движущимся за счет вынужденной конвекции внутри нее. Примем тепловые граничные условия первого рода, т.е. Т_ст = const.

Участки гидродинамической и термической стабилизации.

При входе жидкости в трубу за счет торможения, вызываемого стенками, на них формируется гидродинамический пограничный слой. По мере удаления от входа толщина пограничного слоя возрастает, пока пограничные слои, прилегающие к противоположенным стенам, не сомкнутся. Этот участок называется начальным или участком гидродинамической стабилизации – l_нг.

Подобно изменению профиля скоростей по длине трубы изменяется и профиль температур.

Рассмотрим ламинарное движение жидкости.

Ранее, в разделе дисциплины «Гидродинамика и гидродинамические процессы» [2], нами был рассмотрен гидродинамический начальный участок.

Для определения длины начального участка была предложена следующая зависимость

.

Для жидкости, как известно Pr > 1, следовательно, тепловой пограничный слой будет находиться внутри гидродинамического пограничного слоя. Это обстоятельство позволяет считать, что тепловой пограничный слой развивается в стабилизированном гидродинамическом участке и профиль скорости известен – параболический.

Температура жидкости во входном сечении теплообменного участка постоянна по сечению и равна и в ядре потока она не меняется. При этих условиях уравнение теплового пограничного слоя имеет вид

. (41)

Решение этого уравнения при вышеперечисленных условиях дает:

для длины теплового начального участка

; (42)

для местного коэффициента теплоотдачи

; (43)

для среднего коэффициента теплоотдачи длиной

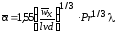; (44)

для местного числа Нуссельта

; (45)

для среднего числа Нуссельта

. (46)

Рассмотрим уравнение (42). Если , то . Для жидкостей Pr > 1, поэтому в большинстве случаев, особенно для жидкостей с большим Pr, теплообмен при ламинарном режиме движения осуществляется в основном на участке термической стабилизации. Как видно из соотношения (43)  для трубы на участке термической стабилизации уменьшается по мере удаления от входа (увеличивается толщина теплового пограничного слоя _т) (рис. 1.6).

Рис. 1.6. Профиль температуры на начальном и стабилизированном участке

при ламинарном течении жидкости в цилиндрической трубе

Рассмотрим турбулентное движение жидкости.

При турбулентном течении потока в трубе, как и на плоской пластине, во-первых, толщины гидродинамического и теплового пограничных слоев совпадают; а во-вторых, растут значительно быстрее, чем для ламинарных. Это приводит к уменьшению длины участков термической и гидродинамической стабилизации, что позволяет в большинстве случаев пренебрегать ими при расчете теплоотдачи

. (47)

. Стабилизированный теплообмен.

Рассмотрим ламинарное движение жидкости

Рассмотрим стационарный теплообмен в круглой трубе, когда теплофизические свойства жидкости постоянны (изотермический случай), профиль скорости не меняется по длине, температура стенки трубы постоянна и равна Т_ст, в потоке отсутствуют внутренние источники тепла, а количество тепла, выделяющееся вследствие диссипации энергии, пренебрежимо мало. При этих условиях уравнение теплообмена имеет такой же вид, что для пограничного слоя. Следовательно, исходным уравнением для изучения теплообмена является уравнение (41).

Граничные условия:

(48)

Решение этой задачи впервые было получено Гретцем, затем Нуссельтом, в виде суммы бесконечного ряда. Несколько иное решение было получено Шумиловым и Яблонским. Полученное решение справедливо и для участка термической стабилизации при условии предварительной гидродинамической стабилизации потока.

Для области стабилизированного теплообмена локальный коэффициент теплоотдачи равен предельному значению

или (49)

Как видно из рисунка (рис. 1.7), с увеличением число Nu уменьшается, асимптотически приближаясь на втором участке кривой к предельному значению Nu_пр = 3,66. Это происходит, потому что для стабилизированного теплообмена профиль температуры по длине трубы не меняется. На первом участке происходит формирование профиля температуры. Первый участок соответствует термическому начальному участку.

Рис. 1.7. Изменение местного и среднего по длине круглой трубы при Т_ст = const

Турбулентное движение жидкости.

Исходное уравнение

. (50)

Граничные условия:

(51)

При решении задачи возникает проблема выбора профиля скорости w_x. Одни для w_x используют логарифмический закон (А.И. Разинов), другие – закон 1/7 (В.Б. Коган). Отмечается консервативность турбулентных течений, которая заключается в слабом влиянии граничных условий и поля скорости w_x на коэффициенты теплоотдачи.

Для числа Нуссельта предлагается следующая формула

. (52)

Как и для ламинарного движения в области стабилизированного теплообмена при турбулентном течении среды Nu не зависит от координаты х.

Нами был рассмотрены выше частные случаи теплообмена, а именно: при изотермической постановке задачи и тепловых граничных условиях первого рода теплообмен в гладких цилиндрических трубах и плоских горизонтальных пластинах.

В литературе имеются решения тепловых задач и для других случаев. Отметим, что шероховатость поверхности трубы и пластины ведет к увеличению коэффициента теплоотдачи.

15. Теплообмен при изменении теплофизических характеристик теплоносителя.

Для жидкого однофазного теплоносителя характерно изменение теплофизических характеристик в зависимости от температуры и давления. Как показывает анализ, существенное изменение вязкости зависит от температуры.

Изменение (T) необходимо учитывать в исходных уравнениях. Если же задача решена без учета (T), то в конечную формулу в виде критериального уравнения вводят множитель .

Множитель учитывает изменение свойств теплоносителя по толщине пограничного слоя. При этом, как известно, меняются профили скорости и температуры в пограничном слое. Индекс «ж» указывает на необходимость использования теплофизических характеристик теплоносителя при температуре ядра потока, а индекс «ст» при температуре стенки. Этот множитель используется также и при обработке экспериментальных данных для жидких теплоносителей.

Учет зависимости плотности от температуры необходим при изучении естественной (свободной) конвекции. Естественная конвекция обусловлена разностью плотностей в различных точках объема жидкости, возникающей вследствии разности температур в этих точках. При этом возникает подъемная сила, которая должна быть учтена в правой части уравнения движения. Наличие естественной конвекции учитывается критерием Грасгофа

. (56)

Здесь  – коэффициент объемного расширения; , Т – температура жидкости в объеме; l – характерный линейный размер.

Критерий Грасгофа характеризует отношение подъемной силы, возникающей в следствии теплового расширения жидкости, к силам вязкости.

Для расчета коэффициента теплоотдачи в условиях естественной конвекции обычно используются зависимости типа

, (57)

при для вертикальной стенки.

Зависимость остальных характеристик (c_p, ) от температуры и давления незначительна.

Часто в процессе теплообмена нагреваемые или охлаждаемые материалы изменяют агрегатное состояние: испаряются, конденсируются, плавятся или кристаллизуются. Особенности таких процессов теплообмена заключаются в том, что тепло подводится к материалам или отводится от них при постоянной температуре и распространяется не в одной, а в двух фазах.

16. Теплоотдача при конденсации пара

Конденсация – процесс перехода вещества из парообразного состояния в жидкое. Основная особенность процесса – тепло подводится и отводится при постоянной температуре.

Теплоотдача при конденсации насыщенных паров представляет собой одновременно перенос теплоты (определяемой теплотой парообразования) и массы (определяемой количеством сконденсированного пара).

Молекулы пара переносятся к охлаждаемой стенке вихрями турбулентного потока, конденсируются, и при этом происходит резкое уменьшение его объема, таким образом, возникает собственное поступательное движение к стенке. Образовавшийся конденсат стекает по стенке, а к стенке подходит свежий пар. Перенос теплоты и основной массы пара к стенке идет настолько быстро, что степень турбулизации потока не оказывает существенного влияния на процесс и не учитывается в расчетах.

На хорошо смачиваемых поверхностях возникает жидкая пленка конденсата, на не смачиваемой (плохо смачиваемой) поверхности образуются капли и струи. При капельной конденсации коэффициент теплоотдачи в несколько раз выше, чем при пленочной конденсации. Однако организация капельной конденсации дороже пленочной. Поэтому на практике используется пленочная конденсация. В процессе теплоотдачи от пара к стенке можно выделить три стадии, каждая из которых обладает собственным сопротивлением:

подвод тепла и вещества от пара к стенке;

собственно процесс конденсации;

перенос тепла через пленку жидкого конденсата.

Первая стадия осуществляется за счет конвективного механизма, обусловленного градиентом давления, возникающим при переходе пара в жидкость, т.е. большой скоростью. Сопротивление второй стадии также невелико.

При пленочной конденсации пара термическое сопротивление сосредоточено в основном в пленке конденсата. Термическое сопротивление пленки определяется механизмом переноса теплоты, зависящим от режима течения конденсата.

По мере стекания пленки конденсата вниз под действием силы тяжести толщина ее будет увеличиваться вследствие увеличения количества конденсированного пара. Следовательно, возникает задача ламинарного течения вязкой жидкости по вертикальной стенке. Конвективное уравнение теплообмена для этого случая будет иметь такой же вид, что и уравнение термического пограничного слоя на начальном участке плоского слоя (24).

Однако упростим задачу. Малая толщина пленки конденсата позволяет считать температурный профиль в слое линейным. Это означает, что количество переданной теплоты через слой конденсата можно трактовать как кондуктивный теплоперенос через плоскую жидкую преграду.

Тогда получим

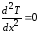. (58)

Граничные условия:

при x = 0 T = T_ст;

при x =  T = T_п.

Интегрирование уравнения (58) с учетом граничных условий дает

, (59)

отсюда

.

Как известно тепловой поток на границе фаз определяется как

. (60)

Из (60) получим . Следовательно, определение коэффициента теплоотдачи сводится к определению толщины пленки конденсата.

Задача определения толщины пленки решена используя балансовые соотношения. Сначала определяется средняя скорость , далее расход конденсата (она по высоте H переменная), далее определяется  и .

Локальное значение коэффициента теплоотдачи  получено в виде

; (61)

осредненное по высоте Н значение

. (62)

Здесь r – теплота конденсации.

Как видно из (61), локальный коэффициент теплоотдачи уменьшается по мере стекания пленки конденсата вследствие увеличения ее толщины.

Зависимость типа (62) может быть получена так же обработкой экспериментальных данных по теории подобия на основе критериального уравнения вида

. (63)

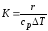
Здесь  критерий Галлилея характеризует отношение сил тяжести к силам вязкого трения;  критерий конденсации (характеризует отношение теплоты фазового перехода к теплоте охлаждения конденсата на твердой стенке).

Для ламинарного режима получено

; (64)

для вертикальной стенки A = 0,94, горизонтальной трубы A = 0,72.

Для турбулентного потока

. (65)

Все физические константы определяются при средней температуре процесса .

Формулы (64) и (65) получены для неподвижного пара. Теплоотдача при конденсации паров зависит от скорости и направления течения паров, от состояния поверхности конденсации, от состава паров и их перегрева. Известно, что  увеличивается, если поток уменьшает  и наоборот. Шероховатость увеличивает  и уменьшает .

Конденсация паровых смесей. При конденсации паровой смеси ее состав меняется, что вызывает изменение температуры конденсации, равной, в конечном счете, температуре конденсации самого низкокипящего компонента смеси. Таким образом, процесс конденсации паровой смеси протекает при переменной разности температур, значение которой зависит не только от физико-химических свойств смеси, но и от структуры потока охлаждающей жидкости и паровой смеси.

Конденсация парогазовой смеси. При наличии в паре даже небольших примесей воздуха или других неконденсирующихся газов  резко уменьшается. Содержание в водяном паре 1  воздуха уменьшает  на 60 , 3  воздуха – на 80 .

Инертные газы скапливаются у поверхности пленки конденсата, возникает дополнительное термическое сопротивление.

17. Теплоотдача при кипении жидкостей

Теплоотдача при кипении жидкостей отличается высокой интенсивностью и часто встречается в промышленной технологии: выпаривание, перегонка жидкостей, испарители и т.д. Для возникновения кипения необходимо, чтобы температура жидкости была выше температуры насыщения и наличие центров парообразования (микроскопические впадины).

Различают кипение на поверхности нагрева и кипение в объеме жидкости. Кипение на поверхности обусловлено подводом теплоты к жидкости от соприкасающейся с ней поверхностью. Кипение в объеме жидкости обусловлено наличием внутренних источников теплоты или значительного перегрева жидкости, возникающего, например, при внезапном снижении давления (ниже равновесного). Наиболее распространенным видом кипения является кипение на поверхности.

Рассмотрим кипение на поверхности.

Для передачи теплоты от стенки к кипящей жидкости необходим перегрев стенки относительно температуры насыщения ∆T = T_ст – T_кип.

На рис. 1.12. показана типичная зависимость коэффициента теплоотдачи и удельной тепловой нагрузки от температурного напора ∆T.

Рис. 1.12. Зависимость коэффициента теплоотдачи  и удельной тепловой нагрузки q

при кипении воды от температурного напора ΔT

В области АВ перегрев мал, мало активных центров парообразования, теплообмен определяется законами свободной конвекции около стенки,  ~ T^1/3. В области ВС перегрева больше, больше центров парообразования,  резко возрастает. Происходит турбулизация пограничного слоя около стенки. Пузыри, поднимаясь и увеличиваясь в объеме, увлекают значительные массы жидкости. На это место поступает новая порция жидкости, таким образом, реализуется циркуляция жидкости. Здесь  ~ T^2/3.

При ∆T ≥ T_кр происходит слияние близко образующихся пузырей. Если l < d пузырька, то на поверхности стенки образуется паровая пленка, создающая дополнительное термическое сопротивление процессу теплоотдачи. Такой режим кипения называется пленочным (рис. 1.13).

Рис. 1.13. Схема пузырчатого кипения

Для воды

Рассмотрим движение пузырька. Достигнув определенного диаметра , пузырек отрывается от твердой поверхности

. (66)

Здесь  и _п – плотность соответственно жидкости и пара;  – краевой угол смачивания,  – коэффициент поверхностного натяжения. В момент отрыва пузырька сила поверхностного натяжения жидкости, которая удерживает пузырек, равна Архимедовой подъемной силе. Поднимаясь, пузырек увеличивается в объеме за счет испарения жидкости внутри пузырька, сплющивается и приобретает форму гриба. Гриб имеет сложную траекторию, дробится и коалесценцируется.

Таким образом, транспорт теплоты при пузырчатом кипении состоит из переноса теплоты от стенки к жидкости, а затем жидкостью теплота передается внутренней поверхности пузырьков в виде теплоты испарения. Передача теплоты от стенки непосредственно пузырю ничтожно мала. Для того, чтобы теплота от жидкости передавалась пузырькам пара, жидкость должна иметь Т несколько выше температуры пара. Поэтому жидкость несколько перегрета относительно температуры насыщенного пара над поверхностью кипящей жидкости.

Скорость переноса теплоты при кипении зависит от физических свойств жидкости, давления, ∆T, свойств материала стенки и т.д.

Учесть все это трудно, трудно предлагать единую зависимость. Поэтому для определения  в литературе предлагаются различные физические модели. Но общепринятой модели нет. Формальный вид

= Aqⁿ, 0,6 < n < 0,7, (67)

где А – сложный комплекс многих величин, влияющих на интенсивность переноса теплоты при кипении. Иногда предлагают критериальное уравнение вида

, (68)

значения A, m, n обычно определяют экспериментально.

18. Тепловое излучение. Радиационно-конвективная теплоотдача.

Во всех телах, температура которых выше 0 K происходит превращение тепловой энергии в лучистую. Носителями лучистой энергии являются электромагнитные колебания. Тепловое излучение аналогично излучению света: поглощается, отражается и преломляется.

Длины волн теплового излучения лежат, в основном, в невидимой (инфракрасной) части спектра и имеют длину 0,8–40 мкм. Световые волны 0,4–0,8 мкм. Твердые тела обладают сплошным спектром излучения: они способны испускать волны всех длин при любой температуре. Интенсивность теплового излучения возрастает с повышением температуры тела, и при T ≥ 600 C лучистый теплообмен между твердыми телами и газами приобретает доминирующее значение.

Когда поток излучения Q_U из окружающей среды попадает на какое-либо тело (рис. 1.14), то в общем случае часть этого потока Q_R отражается от тела, часть Q_A поглощается телом и часть Q_D проходит через тело. Тогда уравнение баланса энергии в общем виде запишется так

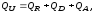(73)

а в долях от общей энергии излучения

Рис. 1.14. Схема тепловых потоков при излучении

Если А = 1 (R и D = 0), тогда тело полностью поглощает все падающие на него лучи, тело абсолютно черное.

Если R = 1(D и A = 0)  полное отражение лучей, тело абсолютно белое.