Часть 1. Продольные волны.

   Допустим, что каждый шарик может двигаться только в направлении вдоль цепочки.

1. Найдите собственную частоту колебаний одного из шариков ω_o, если два соседних закреплены.

2. По цепочке распространяется продольная волна. Найдите сдвиг фаз между колебаниями двух соседних шариков при частоте волн w.

3. При каких частотах колебаний ω по цепочке могут распространяться бегущие волны?

4. Найдите скорость распространения продольной волны по цепочке. Постройте примерный график этой зависимости.

5. Найдите скорость распространения продольной волны при частотах ω << ω_o. Покажите, что полученное выражение можно считать аналогом формулы для скорости звука в упругой среде с = √(E/ρ), где E − модуль Юнга, ρ − плотность среды.

6. В цепочке неподвижно закрепили неподвижно два шарика так, что между ними оказалось n шариков. Определите все частоты собственных колебаний этого участка цепочки, соответствующие различным модам стоячих волн.

Часть 2. Поперечные волны.

   Пусть шарики способны перемещаться только в направлении перпендикулярном цепочке, причем их смещения малы (Δx << l).

1. Определите частоту поперечных колебаний одного шарика, если два соседних закреплены.

2. Найдите скорость распространения поперечной волны по цепочке.

3. Найдите скорость распространения поперечной волны при частотах ω << ω_o. Покажите, что полученное выражение можно считать аналогом формулы для скорости поперечных волн в упругой среде с = √(G/ρ), где G − модуль сдвига, ρ − плотность среды.

4. Найдите минимально возможную длину волны, которая может распространяться по цепочке.

5. На основании качественных рассуждений определите, как зависит скорость распространения поперечной волны от ее амплитуды, когда смещение шариков сравнимо с расстоянием между ними.

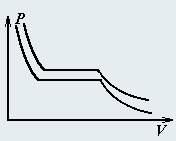
Один моль идеального одноатомного газа совершает циклический процесс, изображенный на рисунке: 1 → 2 прямая, 2 → 1 − адиабата.

1. Найдите отношение V₁/V_o.

2. Какова максимальная температура газа в цикле?

3. Постройте примерный график зависимости теплоемкости газа на участке 1 → 2 от его объема.

4. Постройте график зависимости количества теплоты, полученной газом при расширении на участке 1 → 2, от его объема.

5. Найдите КПД цикла.

 Рассмотрите свойства идеального кристалла с кубической решеткой, образованного одинаковыми атомами массой m. Потенциальная энергия взаимодействия двух атомов в кристалле зависит от расстояния между их центрами r по закону

U(r) = a/r¹² − b/r⁶,

где a, b − некоторые положительные константы. Сила взаимодействия двух атомов связана с потенциальной энергией соотношениемF = −U_r^/, где U_r^/ − производная энергии по r. При расчете всех характеристик можно учитывать взаимодействие атома только с его ближайшими соседями.    Выразите через параметры a, b, m следующие характеристики кристалла:

1. Плотность ρ.

2. Удельную теплоту сублимации (перехода из кристаллического в газообразное состояние) λ.

3. Модуль Юнга кристалла E.

4. Максимальное относительное удлинение кристалла до его разрушения ε_пр.

5. Предел прочности на разрыв (максимальное механическое напряжение, который может выдержать кристалл без разрушения) − σ_пр.

6. Линейный коэффициент термического расширения кристалла α.

   Рекомендуем использовать приближенную формулу, справедливую при малых величинах x:

(1 + x)^α ≈ 1 + αx + α(α − 1)x²/2,

в которой вы можете использовать столько членов, сколько требуется в конкретной ситуации.

 На рисунке изображены две изотермы вещества, совершающего фазовый переход газ-жидкость, соответствующие двум очень близким температурам T и T + ΔT. Рассмотрите цикл Карно между горизонтальными участками изотерм.

   1. Покажите, что уравнение (которое называется уравнением Клапейрона-Клаузиуса), связывающее изменение давления насыщенных паров изменением температуры имеет вид

Δ/ΔT = q/{T(V₁ − V₂)};

где обозначено: λ − удельная теплота перехода, V₁ и V₂ − удельные объемы газовой и жидкой фаз, соответственно.    2. Считая изменения ΔP и ΔT бесконечно малыми, полагая q независящим от температуры, V₂ < < V₁, считая пар идеальным газом, найдите зависимость давления насыщенных паров воды от температуры.    3. Представьте полученную зависимость в таких координатах, чтобы она была линейной. В таблице задана зависимость давленияp насыщенных паров воды от температуры t. Используя все приведенные данные, найдите удельную теплоту парообразования воды.

t, °C	10	20	30	50	80	100
p, Па	1226	2333	4240	12330	47343	101325

   4. Воспользуйтесь полученным в пункте 1 уравнением для описания фазового перехода жидкость − твердое тело. Найдите на сколько надо изменить давление, чтобы температура замерзания льда изменилась на один градус. Удельная теплота плавления льда равна 332 кДж/кг.

   При постоянной температуре T зависимость давления газа P от высоты h, определяется барометрической формулой

P = P_oe^−μgh/(RT),

где μ − молярная масса газа, g − ускорение свободного падения, R − газовая постоянная. Молярную массу воздуха принять равной μ = 0,029 кг/моль.    1. Оцените высоту, на которой давление воздуха уменьшается на 1 %, если температура воздуха постоянна и равна t = 0 °C.    2. В очень высоком вертикальном цилиндрическом закрытом сверху сосуде с площадью основания S находится воздух, масса которого равна m. Найдите зависимость давления газа на дно сосуда от высоты сосуда и от температуры газа.    Рассмотрите два предельных случая а) μgh > > RT; б) μgh < < RT. Дайте физическое объяснение полученным результатам.    Постройте семейства графиков зависимостей давления газа на дно сосуда от температуры (для нескольких значений высоты сосуда h) и от высоты сосуда (при различных значениях температуры T).

   В качестве наглядной модели газа часто рассматривают множество маленьких жестких шариков, хаотически движущихся в некотором сосуде. В дальнейшем рассмотрим поведение упругого шарика движущегося вертикально в закрытом сосуде, находящемся в поле тяжести Земли. Столкновения шарика с дном и верхней крышкой сосуда будем считать абсолютно упругими. Будем изучать среднюю силу давления шарика на дно сосуда, причем будем полагать, что усреднение проводится по промежутку времени, значительно превышающему время между двумя последовательными ударами шарика.    3. Найдите зависимость силы давления шарика на дно сосуда от его высоты h и его скорости v_o у дна сосуда.    Рассмотрите предельные случаи а) mgh > mv_o²/2; б) mgh < mv_o²/2. Постройте семейства зависимостей силы давления от высоты сосуда (при постоянной v_o) и от квадрата скорости v_o² (при постоянной высоте сосуда h).    4. Рассмотрите «адиабатный» процесс уменьшения высоты сосуда с прыгающим шариком. Пусть крышка сосуда медленно опускается, найдите зависимость силы давления шарика на дно от высоты сосуда. Определите «показатель» адиабаты для этой системы. Дайте объяснение полученному результату.

  1. Электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q₁ и −q₂. Покажите, что поверхность нулевого потенциала этого поля представляет собой сферу, найдите ее радиус.    2. Точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Найдите:    − суммарный индуцированный заряд сферы;    − силу взаимодействия заряда и сферы.    3. Точечный заряд q расположен на расстоянии l от центра металлической изолированной сферы радиуса R. Найдите:    − индуцированный дипольный момент сферы;    − силу взаимодействия заряда и сферы.    4. Точечный заряд q находится на расстоянии h от бесконечной плоской проводящей пластины. Найдите:    − распределение поверхностной плотности индуцированных зарядов на платине;    − силу взаимодействия заряда и пластины;    − энергию взаимодействия заряда и пластины;    5. Внутри равномерно заряженного шара с объемной плотностью заряда ρ вырезана сферическая полость, центр которой находится на расстоянии a от центра шара. Найдите напряженность электрического поля в полости.

   6. Металлический шарик радиуса r помещен в однородное электрическое поле напряженности E. Найдите:    − распределение поверхностной плотности зарядов на шарике;     − индуцированный дипольный момент шарика.    7. «Газ» состоит из одинаковых металлических шариков радиуса r, концентрация которых равна n. Среднее расстояние между шариками значительно больше их радиусов. Найдите диэлектрическую проницаемость такого «газа».    Указание. Воспользуйтесь соотношением

ε × ε_o × E = ε_o × E + P,

где P − поляризация среды (дипольный момент единицы объема).    Диэлектрическая проницаемость воздуха при нормальных условиях равна ε = 1,00058. Оцените средний размер молекул воздуха.    8. Точечный заряд q находится на расстоянии h от бесконечной плоской границы с бесконечным диэлектриком с проницаемостью ε. Найдите    − распределение поверхностной плотности поляризационных зарядов на платине;    − силу взаимодействия заряда и пластины.    9. Шар радиуса r, изготовленный из диэлектрика с проницаемостью ε, помещен в однородное электрическое поле напряженностиE. Найдите:    − распределение поверхностной плотности зарядов на шарике;    − индуцированный дипольный момент шарика.    10. Небольшой шарик радиуса r, изготовленный из диэлектрика с проницаемостью ε, находится на большом расстоянии l (l > > r) от точечного заряда q. Найдите силу, действующую на шарик со стороны заряда.

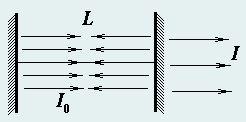
 Цепочка резисторов состоит из N одинаковых звеньев и подключена с одной стороны к источнику постоянного напряжения U_o, а с другой к источнику постоянного напряжения U₁.    Для построения требуемых графиков используйте следующие значения параметров R₂ = 20R₁, U_o = 2U₁.

1. Найдите значения напряжений на всех резисторах R₂. Постройте схематический график зависимости напряжения от номера резистора.

2. Найдите значения напряжений на резисторах R₂, если источник U₁ отключить. Постройте схематический график зависимости напряжения от номера резистора.

3. Найдите значения напряжений на резисторах R₂, если источник U₁ заменить на резистор сопротивлением r.

4. Найдите значения напряжений на всех резисторах R₂ при N → ∞.

5. Найдите сопротивление цепи, состоящей из N звеньев. Рассмотрите случай N → ∞.

6. Допустимая погрешность расчета сопротивления цепи, состоящей из N звеньев равна ε(ε < < l). При каком числе звеньев цепочку можно считать бесконечной? Получите результат в общем виде, а затем проведите численный расчет для а) R₂ = 20R₁; б) R₂ = 2R₁ при предельной погрешности e = 1 %.

7. Данная задача является прекрасной моделью для описания кабеля с небольшой утечкой. При этом сопротивления R₁описывают собственное сопротивление кабеля, а R₂ − сопротивление окружающей среды, по которой возможна некоторая утечка электрического тока.

   Очень длинный медный провод диаметром a = 1 мм, покрытый слоем лака толщиной h = 20 мкм, находится в хорошо проводящей среде. Потенциал одного конца провода поддерживают равным φ_o = 100 В. Найдите зависимость силы тока в проводе от расстояния до источника x. Чему равна сила тока, потребляемая от источника? На каком расстоянии сила тока уменьшится в два раза?    Удельное электрическое сопротивление меди принять равным ρ₁ = 2 × 10⁻⁸ Ом•м, удельное электрическое сопротивление покрывающего лака ρ₂ = 2 × 10⁸ Ом•м.

   Вертикальная катушка содержит N витков, высота катушки H, ее радиус a. На оси катушки находится тонкий деревянный стержень толщиной b, b < < a, по которому может скользить без трения проводящее кольцо, радиус которого чуть превышает радиус стержня. Электрическое сопротивление кольца R, индуктивность L, масса m. Если по катушке протекает переменный электрический ток круговой частоты ω с амплитудным значением силы тока I_o, то кольцо приподнимается над катушкой.    В пунктах (1) − (4) считать, что по катушке протекает постоянный электрический ток силой I.

   1. Найдите величину индукции магнитного поля, создаваемого одним витком катушки, на оси витка в зависимости от расстояния до центра витка.    2. Найдите зависимость индукции магнитного поля B на оси катушки от расстояния до нее h. При вычислениях воспользуйтесь формулой

∫{dx/(a² + x²)^3/2} = x/{a²√(a² + x²)}.

   3. Считая, что h << a << H, представьте полученное выражение для индукции поля в приближенном виде B = B_o(1 + βh).    Найдите значения постоянных B_o и β.    В дальнейших пунктах используйте это приближенное выражение.    4. Найдите горизонтальную составляющую индукции магнитного поля на малом расстоянии b от оси катушки на высоте h.    Далее будем считать, что по катушке протекает переменный электрический ток круговой частоты ω с амплитудным значением силы тока I_o.    5. Пусть кольцо находится на высоте h. Найдите значение силы тока в кольце и сдвиг фаз между током в кольце и током в катушке.    6. Найдите среднюю силу, действующую на кольцо, со стороны магнитного поля.    7. Считая высоту подъема кольца малой по сравнению с высотой катушки, покажите, что зависимость высоты подъема кольца от силы тока в катушке имеет вид h = A − B/I_o². Запишите выражения для параметров A, B.

• Следующая задача

  1. На двух проводящих горизонтальных параллельных рельсах, находящихся на расстоянии l друг от друга, перпендикулярно рельсам расположена проводящая перемычка массы m, которая может скользить по рельсам без трения. Вся система помещена в однородное вертикальное магнитное поле индукции B. Рельсы соединили с помощью резистора сопротивлением R, а к перемычке приложили постоянную горизонтально направленную силу F. Пренебрегая сопротивлением перемычки и рельсов и индуктивностью контура, найдите скорость установившегося движения перемычки.

   2. В системе, описанной в п. 1, резистор заменили на конденсатор емкости C. Как будет двигаться перемычка в этом случае?

   3. Замените в рассматриваемой системе конденсатор на катушку индуктивностью L и определите характер движения перемычки в этом случае.

   4. В установке, описанной в п. 1, перемычка покоится на некотором расстоянии x_o от резистора. Внешняя сила не действует, первоначально магнитного поля нет, а затем достаточно быстро включают вертикальное однородное магнитное поле индукции B. Как изменится расстояние между перемычкой и резистором по прошествии большого промежутка времени.

• Следующая задача

 В различных приборах для фокусировки заряженных частиц используется магнитное поле. В данной задаче изучаются условия фокусировки частиц.    1. Частица массы m влетает в магнитное поле индукции B со скоростью v, направленной под углом γ к вектору индукции поля. Покажите, что траектория частицы является цилиндрической спиралью, определите ее радиус R и шаг h.    2. Пучок частиц массы m вылетает из узкой щели, расположенной в плоскости XY. Скорости всех частиц равны v и направлены в пределах плоского малого угла 2α_o, биссектриса которого перпендикулярна плоскости XY. Над плоскостью создано однородное магнитное поле индукции B, направленное параллельно пластине. Считая, что вектора скоростей всех частиц направлены перпендикулярно вектору индукции поля, покажите, что частицы будут фокусироваться на пластине. Определите положение и ширину полосы, в пределах которой частицы будут попадать на пластину.

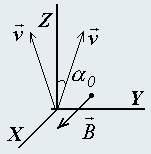
   3. Определите форму и размеры области попадания частиц на пластину в условиях, описанных в п. 2, если вектора скоростей частиц направлены внутри конуса с углом полураствора α_o.    4. Пучок частиц массы m, влетает из одной точки в однородное магнитное поле индукции B, направленное вдоль оси Z. Скорости частиц равны v, а вектора скоростей частиц направлены внутри конуса с углом полураствора α_o, ось которого совпадает с направлением вектора индукции поля. Найдите ширину пучка как функцию координаты z. Считая угол α_o малым, найдите на каком расстоянии от источника частицы сфокусируются. Оцените ширину пучка в области фокуса.

 Опишите прохождение световых лучей через центрированную оптическую систему состоящую из сферических преломляющих поверхностей, центры которых лежат на одной прямой, которая называется оптической осью системы. Заметим, что таким системам относятся телескопы, микроскопы, фотоаппараты, диапроекторы, глаза человека и т.д. Такие системы обладают осевой симметрией, поэтому достаточно рассмотреть ход лучей в одной плоскости, содержащей оптическую ось.    Пусть (см. рис. 1) OO₁ – оптическая ось системы, проведем произвольную плоскость P, перпендикулярную оси. Произвольный лучAB, пересекающий плоскость P однозначно определяется двумя параметрами: x – расстоянием от оптической оси до точки пересечения луча и плоскости, α – углом между направлением луча и оптической осью (договоримся отсчитывать этот угол в направлении «против хода часовой стрелки»). Очевидно, что параметры луча (x, α) могут быть как положительными так и отрицательными. Кроме того, будем полагать их малыми настолько, что везде, где это необходимо, будем считать синус и тангенс угла α равным величине самого угла, естественно, измеренному в радианах. Такое приближение называется параксиальным (близким к оси). В данном приближении в любой центрированной системе связь между параметрами одного и того же луча в разных плоскостях линейна, сколько бы преломляющих поверхностей не находилось между ними. Рассмотрите изменение этих параметров, когда луч проходит через следующие простые элементы оптической системы.

   1. Участок пустого пространства. Пусть между двумя плоскостями P_o (входной) и P₁ (выходной), находящихся на расстоянии dдруг от друга, преломляющих поверхностей нет (рис. 2). Установите связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча.

   2 Сферическая преломляющая поверхность. Луч преломляется на сферической поверхности радиуса R, за которой находится среда с относительным (второй среды относительно первой) показателем преломления n. Установите связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча.    3. Тонкая линза. Линза представляет собой две сферические поверхности, она считается «тонкой», если можно пренебречь горизонтальным смещением луча в самой линзе, иными словами, если ее толщина значительно меньше радиусов кривизны ее поверхностей. Покажите, что связь между выходными (x₁, α₁) и входными (x_o, α_o) параметрами луча, прошедшего через тонкую линзу, с радиусами кривизны поверхностей R₁, R₂ и показателем преломления n, выражается формулами

x₁ = x_o

α₁ = −(n − 1) × (1/R₁ + 1/R₂) × x_o + α_o.

   4. Используя результаты п. 3, получите формулу для фокусного расстояния F тонкой линзы.    5. Получите «формулу тонкой линзы», связывающую расстояние от предмета до линзы a с расстоянием от линзы до изображения b:

1/a + 1/b = 1/F.

   6. Рассмотрите оптическую систему состоящую из двух сферических зеркал, повернутых навстречу друг другу (рис. 3). Обозначим радиусы кривизны одного зеркала R₁ (его центр точка O₁); другого – R₂ (центр – O₂); расстояния между зеркалами – d. Цель исследования – выяснить при каких параметрах системы произвольный световой луч AB не будет покидать данную оптическую систему.

   Рассматриваемая нами система является оптическим резонатором, повсеместно используемым в оптических квантовых генераторах (лазерах). Если для него выполняется условие задачи, то такой резонатор называется устойчивым, в противном случае неустойчивым.    Заменим систему зеркал на бесконечную цепочку линз (рис. 4), фокусные расстояния которых равны фокусным расстояниям зеркал, которые, в свою очередь, известны:

F₁ = R₁/2; F₂ = R₂/2.

   Понятно, что такая система полностью эквивалентна резонатору.

   6.1. Используя линейные преобразования, полученные ранее, запишите формулы преобразований для произвольного луча за полный проход резонатора. Выразите формулы этих преобразований через безразмерные параметры, определяющие геометрию оптической системы

ξ₁ = 1 − d/R₁; ξ₂ = 1 − d/R₂.

   6.2. В некоторых случаях явные выражения для параметров луча могут быть представлены в виде x_n = A × γⁿ; y_n = B × γⁿ, где γ– некоторая постоянная. Выразите возможные значения этого параметра параметры системы ξ₁, ξ₂.    При каком соотношении между параметрами ξ₁, ξ₂, резонатор будет устойчивым? Изобразите область устойчивости на диаграмме (ξ₁, ξ₂).

• Следующая задача

  «Объясняя» возникновение радуги, авторы учебных пособий весьма часто ограничиваются указанием на то, что это замечательное природное явление демонстрирует явление дисперсии света. Иногда приводят типичный рисунок двойного преломления луча света в сферической капле воды (рис. 1), позаимствованный еще из работы Р.Декарта. Приведенные утверждения справедливы: действительно изображение радуги формируют солнечные лучи, дважды преломившиеся на поверхности капли (и конечно, один раз отразившиеся от ее внутренней поверхности); действительно показатель преломления воды зависит от длины волны падающего света, поэтому углы выхода лучей из капли различны для различных длин волн. Однако объяснение и описание радуги не столь просто, как это кажется на первый взгляд, хотя эффекты данного явления вполне объяснимы в рамках геометрической оптики.

   Рассмотрим прохождение лучей через сферическую каплю.

   Назовем оптической осью прямую O₁O₂, проходящую через центр капли и параллельную падающему лучу S_o. Обозначим:    S₁ – луч, сразу отразившийся от поверхности капли;    S₂ – луч, испытавший два преломления на поверхности капли;    S₃ – луч, испытавший два преломления и одно отражение внутри капли;    S₄ – луч, испытавший два преломления и два отражение внутри капли.    Углы, под которыми лучи отходят от капли θ₁, θ₂, θ₃, θ₄, будем отсчитывать от оптической оси. Назовем прицельным параметромρ отношение расстояния между падающим лучом и оптической осью к радиусу капли. (Для лучей, падающих на каплю, этот параметр изменяется от −1 до +1).    1. Найдите зависимости углов, под которыми лучи отходят от капли θ₁, θ₂, θ₃, θ₄, от прицельного параметра ρ.    2. Покажите, что зависимости углов θ₁, θ₂ от прицельного параметра ρ являются монотонными. Покажите, что для лучей S₃, S₄существуют минимальные значения углов отклонения θ₃, θ₄. Найдите значения этих минимальных углов.    3. Покажите, что лучи, вышедшие из различных капель под одинаковыми углами к оптической оси, расположенных в разных точках пространства, дают изображение на сетчатке глаза в виде дуги окружности. Постройте ход этих лучей в глазу человека.    4. Покажите, что минимальным углам отклонения соответствует яркая граница, которая определяет угловой размер радуги.    5. Вычислите угловой наблюдаемый размер α основной и вторичной радуги. (На рис. 3 показана только одна из них).

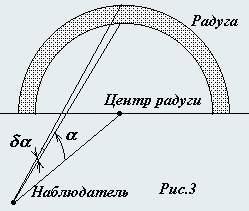
   6. Вычислите угловую ширину δα каждой дуги радуги.    Значения показателя преломления воды, для различных длин волн.    Длина волны (нм), цвет: 759,0 (красный); 589,8 (желтый); 486 (голубой); 397,0 (фиолетовый)    Показатель преломления: 1,329; 1,333; 1,337; 1,344

• Следующая задача

  В интерференционной схеме Юнга две узкие параллельные щели S₁ и S₁, расстояние между которыми равно a, освещаются плоской волной, падающей нормально на экран со щелями. На расстоянии L(L >> a) расположен экран, на котором наблюдается интерференционная картина. Исследуется зависимость интенсивности света на этом экране от координаты x(x << L) − расстояния до оси симметрии системы.

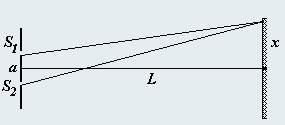
   1. Щели освещены монохроматической волной с длиной волны λ. Найдите распределение интенсивности света на экране. Определите ширину интерференционной полосы (расстояние между двумя последовательными максимумами интенсивности).    2. Пусть щели освещены двумя монохроматическими волнами равной интенсивности с близкими длинами волн λ и λ + Δλ (Δλ >> λ). Опишите распределение интенсивности света на экране в этом случае.    3. Щели осветили немонохроматическим излучением, содержащим непрерывный спектр длин волн, лежащих в узком интервале отλ_o и λ_o + Δλ (Δλ >> λ_o). Опишите распределение интенсивности света на экране в этом случае.    4. Рассмотрим следующую модель частично когерентного света. Световой поток представим в виде случайной совокупности цугов − ограниченных во времени и пространстве участков синусоидальных волн. Все цуги имеют одинаковую частоту, амплитуду и длительность τ. Однако начальные фазы колебаний изменяются от цуга к цугу случайным образом.

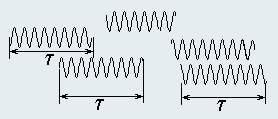
   Опишите интерференционную картину на экране в интерференционной схеме Юнга, если щели освещены частично когерентным светом, модель которого представлена выше. Покажите, что качественно интерференционная картина совпадает с картиной, описанной в п.3. Установите связь между величинами τ и Δλ (а также с шириной спектра Δv), чтобы две описанные интерференционные картины качественно совпадали.

• Следующая задача

   Все взаимодействия, все сигналы распространяются с конечной скоростью, поэтому любая воспринимаемая нашими органами чувств и приборами информация «запаздывает»: то, что мы видим «сейчас», на самом деле произошло «раньше». Нам повезло − скорость света настолько велика, что упомянутое «запаздывание» практически не оказывает никакого влияния на наше поведение. Тем, не менее, в некоторых случаях его необходимо учитывать. Этой проблеме и посвящена данная задача.

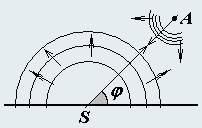
   Положение некоторого движущегося тела A (объекта наблюдения) с помощью сонара (звукового радара) S. Сонар посылает очень короткий звуковой сигнал в виде изотропной сферической волны и улавливает отраженную от тела волну. Скорость распространения волны известна и равна c.    Сонар фиксирует следующие величины:    время, когда послан сигнал − t_o; время прихода отраженной волны − τ, направление на точку, из которой пришел отраженный сигнал, задаваемое с помощью угла φ.    Будем считать, сигналы сонара каким-то образом различаются, поэтому компьютер сонара в момент регистрации отраженного сигнала, точно «знает», когда именно этот сигнал был послан. Затуханием сигнала можно пренебречь.    Введем систему координат xOy, начало которой совместим с сонаром. Будем рассматривать тела, движущиеся в этой плоскости.

   Для определения положения тела приняты следующие правила: положение тела в момент прихода отраженного сигнала задается измеренным углом φ, а расстояние до него рассчитывается по формуле

r^/ = (τ − t_o)c/2. (1)

   Определенное по этим правилам положение тела будем называть изображением объекта.    1. Пусть наблюдаемое тело движется равномерно вдоль оси OX. Закон движения тела имеет вид

x = x_o + v_ot. (2)

   1.1. Определите скорость движения изображения тела.    1.2. Найдите закон движения изображения.    2. Наблюдаемое тело движется равноускоренно вдоль оси OX. Закон движения тела имеет вид

x = at²/2. (3)

   2.1. Определите скорость и ускорение движения изображения тела, как функции времени. Постройте примерные графики этих зависимостей.    2.2. Найдите закон движения изображения.    3. Наблюдаемое тело движется в плоскости xOy по закону известному закону

x = x(t), y = y(t). (4)

   3.1. Получите общее уравнение, связывающее время отправления сигнала t_o и время прихода отраженного сигнала τ.    3.2. Покажите, что траектория движения изображения совпадает с траекторией движения тела.    3.3. Считая, что скорость сигнала значительно превышает скорость движения наблюдаемого тела и время распространения сигнала также является малой величиной, получите приближенные явные выражения для определения координат изображения, учитывающие малые поправки, связанные с запаздыванием, только первого порядка по малому параметру γ = v/c.    4. Пусть наблюдаемое тело движется по закону

x = v_ot, y =l. (5)

   4.1. Найдите зависимость скорости движения изображения тела от времени. Постройте примерный график этой зависимости.    4.2. Найдите зависимость скорости движения изображения тела от его наблюдаемой координаты x^/. Постройте примерный график этой зависимости.    5. Предложите правила определения закона движения тела, дающие точный результат при определении закона движения наблюдаемого объекта.

• Следующая задача

 Движение со сверхзвуковой скоростью − давняя мечта авиаконструкторов. Однако при таких скоростях возникает ряд неожиданных эффектов, исследовать которые − ваша задача.    1. Самолет движется горизонтально на высоте h над поверхностью земли (Землю считайте плоской) с постоянной скоростью V. Наблюдатель находится в точке C на поверхности земли.

   Совместим ось Ox с траекторией движения самолета, ось Oy направим вертикально, проходящую через точку наблюдателя. Закон движения самолета запишем в виде

x = Vt. (1)

   Скорость звука в воздухе известна и равна c.    1.1. В какой момент времени τ звуковая волна, испущенная самолетом в точке с координатой x, достигнет наблюдателя?    1.2. Постройте примерные графики зависимости времени прихода волны от координаты точки ее испускания τ(x) для значений следующих скорости самолета:

V₁ = 0,10c; V₂ = 0,50c; V₃ = c; V₄ = 1,5c; V₅ = 2,0c.

   Считайте, что t ∈ [− ∞, +∞].

   2. «Гудящий» самолет начинает двигаться из начала координат в момент времени t = 0. Временем разгона самолета можно пренебречь.    2.1. Определите область пространства (множество точек (x, y)), до которой дошла звуковая волна к моменту времени t. Для аналитического описания этой области можете выбрать ту форму, которая вам нравится.

   2.2. Постройте эту область для следующих значений скорости движения самолета:

V₁ = 0,50c; V₃ = c; V₅ = 2,0c.

   3. В качестве характеристики звуковой волны примем отклонение давления воздуха Δp от среднего давления. Будем также считать, что неподвижный самолет испускает сферическую монохроматическую волну с частотой ν _o. Пусть самолет движется так, как описано в пункте 1. Считайте, что амплитуда звуковой волны убывает обратно пропорционально расстоянию до источника.    3.1. Запишите выражение для величины Δp в точке наблюдения, как функцию времени.

   3.2. Постройте примерный график зависимости частоты звука, воспринимаемого наблюдателем, от времени. Предварительно дайте ваше определение «частоты в данный момент времени». Рассмотрите следующие значения скорости движения самолета:

V₁ = 0,50c; V₃ = c; V₅ = 2,0c.

   3.3. Пусть звук самолета пришел из точки A, направление на которую задается углом α над горизонтом. Найдите зависимость частоты пришедшего звука от этого угла.    4. Узкий пучок электронов движется в воде со скоростью V = 0,90c, где с − скорость звука в вакууме. Торможением электронов можно пренебречь.

   Показатель преломления воды n = 1,33. При движении электронов возникает свечение Вавилова − Черенкова. На оси пучка и перпендикулярно ему расположена собирающая линза радиуса r = 5,0 см с фокусным расстоянием F = 50 см, на расстоянии a = 45 см за ней плоский экран.    Укажите область экрана, освещенную, благодаря излучению электронов.

• Следующая задача

 Водопроводный смеситель холодной (T₁ = 10 °C) и горячей (T₂ = 70 °C) воды состоит из двух одинаковых труб AB и CB, переходящих в удлинитель BD (рис.). Краны K₁ и K₂ регулируют расход q (т.е. объем воды, проходящий через трубу в единицу времени) и температуру T воды, выходящей из смесителя.    Опыт показывает, что расход воды через трубу AB (или CB) пропорционален разности гидростатических давлений p_A и p_B на ее концах q = αC(p_A − p_B), где α − некоторый безразмерный коэффициент «открытия крана», принимающий значение от нуля (кран закрыт) до единицы (кран полностью открыт), а C − некоторый постоянный размерный коэффициент для данной трубы.

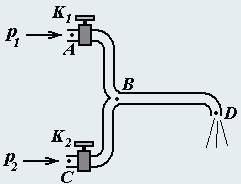
   Расход воды через удлинитель BD также пропорционален разности давлений жидкости на его концах q = C(p_B − p₀), где p₀ − нормальное атмосферное давление на выходе из трубы в точке D (см. рис.).    Давления в магистралях холодной p₁ = p_A = 3,0 атм. и горячей p₂ = p_В = 2,6 атм. труб поддерживаются постоянными. Воду будем считать несжимаемой жидкостью, а потери теплоты при прохождении смесителя − пренебрежимо малыми.    Если полностью открыть (α₁ = 1,0) кран холодной воды при полностью закрытом кране горячей воды, то расход воды будет равен q₁ = 1,4 л/с.

1. Вычислите значение коэффициента C и укажите его размерность.

2. Найдите расход q₂ воды при полном открытии крана с горячей водой (при закрытом втором кране).

3. Вычислите расход воды q₃ и ее температуру T₃ в случае, когда два крана открыть полностью (α₁ = α₂ = 1,0).

4. Найдите расход воды q₄ и ее температуру T₄ в случае, когда один кран холодной воды открыт на α₁ = 0,30, а кран горячей − на α₂ = 0,70.

5. В «час пик» при большом количестве пользователей давление p₂ в магистрали горячей воды может значительно упасть. При каком давлении p_2min подача горячей воды в смеситель полностью прекратится, если кран холодной воды открыт на α₁ = 0,30, а кран горячей − на α₂ = 0,70?

• Следующая задача

Часто простейшие модели позволяют достаточно эффективно описывать сложные механические системы. Например, при прыжке человек приседает, слегка нагнувшись, затем толкается ногами, распрямляет корпус и, собственно, … взлетает! Попробуем описать этот процесс с помощью «гантельной» модели человека с нежесткой связью.    Представим человека в виде упрощенной механической модели, состоящей из двух одинаковых грузов некоторой массы, расстояние между которыми может регулироваться человеком сознательно по требуемому закону (Рис. 1).

   В рамках этой модели прыжок человека вверх описывается следующим образом: верхний груз опускают на расстояние h = 30 см(человек приседает). Затем «включаются» «мышцы ног», развивающие постоянную вертикальную силу F = η × mg, где η − некоторый постоянный безразмерный «коэффициент перегрузки», действующую между грузами. По достижении верхним грузом исходного положения работа мышц прекращается, и расстояние между грузами при дальнейшем движении остается неизменным. Для расчета примите, что η = 7,0.

   1. Вычислите максимальную высоту H₁, на которую поднимется нижний груз при подобном прыжке. Чему равно время t₁отталкивания от плоскости? Вычислите КПД К прыжка в рамках данной модели.    2. Предположим, что человек помещен на массивную горизонтальную платформу, совершающую гармонические колебания с амплитудой A = 20 см и частотой ν = 1,0 Гц (Рис. 2).

   Человек может подпрыгнуть в произвольной точке траектории, причем можно считать, что параметры прыжка будут аналогичны параметрам в пункте 2.1 задачи. На какую максимальную высоту H₂ может подпрыгнуть человек с массивной платформы?    3. В рамках данной модели рассмотрим раскачивание человека на качелях длиной L методом «сел-встал» (рис. 3).

   Суть метода проста: в одних нужных точках траектории нужно вставать, а в других − садится, причем в процессе движения человек от качелей не отрывается. Будем считать, что при вставании человека масса m приближается к оси вращения на расстояниеh = 0,10L (h << L), а при приседании она возвращается обратно. Предположим качели отклонили на угол α_o = 10° и отпустили. На какой максимальный угол α могут отклониться качели за один период колебаний?    4. При тренировке космонавты крутят «солнышко», делая полный оборот в вертикальной плоскости на качелях длиной L. В нижней точке траектории угловая скорость вращения космонавта ω_o. Методом «сел-встал», описанным в предыдущем пункте задачи, космонавт может изменить угловую скорость ω вращения качелей за один оборот. Причем это нужно делать циклически, возвращаясь в исходное положение в нижней точке траектории. На какую величину Δω космонавт может увеличить угловую скорость вращения в нижней точке траектории методом «сел-встал» за один оборот качелей? Время вставания и приседания считайте достаточно малым.

   Примечание: при вращательном движении в отсутствие моментов внешних сил справедлив закон сохранения момента импульса: произведение импульса p материальной точки на расстояние до оси вращения r есть величина постоянная

m₁v₁r₁ = m₂v₂r₂ ⇔ m₁ω₁r₁² = m₂ω₂r₂².

Многие свойства кристаллов могут быть объяснены на основе законов классической физики. В данном задании вам необходимо оценить некоторые характеристики ионного кристалла, в качестве которого рассматривается кристалл поваренной соли NaCl.

   Кристаллическая решетка поваренной соли является простой кубической, то есть ионы разных знаков (положительные Na⁺(относительная атомная масса A_rNa = 23) и отрицательные Cl⁻ (A_rCl = 35)) расположены в узлах кубической решетки. Радиусы этих ионов приблизительно равны.    В данном задании эти ионы следует рассматривать как жесткие равномерно заряженные непроводящие сферы одинаковых радиусов. При расстояниях между ионами большими или равными диаметру иона взаимодействие между ними является чисто электростатическим

   Часть 1. «Ионные радиусы»    Плотность поваренной соли равна ρ = 2,16 × 10³ кг/м³. Определите средний ионный радиус рассматриваемых элементов.    Часть 2. «Растворимость»    2.1. Рассчитайте энергию взаимодействия одного иона кристалла со всеми остальными.    2.2. Кристаллы поваренной соли могут растворяться в различных жидкостях, полностью распадаясь на отдельные ионы. Оцените, какова должна быть минимальная диэлектрическая проницаемость жидкости ε_min, чтобы соль могла растворяться в ней.    2.3. Диэлектрическая проницаемость воды равна ε = 81. Рассчитайте удельную теплоту растворения (количество теплоты, выделяющейся при растворении единицы массы) поваренной соли в воде.    Заряд электрона e = 1,6 × 10 ⁻¹⁹ Кл, постоянная Авогадро N_A = 6,02 × 10²³ моль⁻¹.    Диэлектрическая постоянная ε_o = 8,85 × 10 ⁻¹² Ф/м.    При решении задачи Вам может пригодиться следующая сумма:

   Если же Вы столкнетесь с ещё какой-либо трудно вычисляемой суммой, обозначьте ее буквой, которая Вам нравится.

• Следующая задача

  На горизонтальной плоскости находится цилиндрическая труба, радиусом R. Какую минимальную скорость необходимо сообщить телу, находящемуся на горизонтальной плоскости, чтобы перебросить его через цилиндрическую трубу?

   Решение:    Траектория тела − это парабола, которая касается цилиндра в симметрично расположенных точках B и B^/ на двух сторонах ствола (рис.).

   Тело удаляется от точки бросания с начальной скоростью v₁ под углом α к горизонту. В точках касания B и B^/ скорость тела v₂составляет угол β с горизонталью.    Выберем угол β в качестве независимой переменной задачи. Тогда в точке B вертикальная составляющая скорости равна

v₂sinβ = gt₂,

где t₂ − время полета на участке BC траектории (C − максимальная точка подъема, максимум параболы). Соответствующее горизонтальное перемещение BF равно

v₂t₂cosβ = Rsinβ.

После перемножения этих двух уравнений получаем

v₂² = gR/cosβ.

   Закон сохранения энергии при полете между точками A и B дает

mv₁²/2 = mv₂²/2 + mg(R + Rcosβ),

или

v₁² = v₂² + 2gR(1 + cosβ) = gR/cosβ + 2gR(1 + cosβ).

   Мы получили выражение для начальной скорости в виде

v₁² = 2gR(1 + cosβ + 1/(2cosβ))

и можем вычислить минимальное значение v ₁, используя дифференциальное исчисление. Приравняв производную

d(1 + cosβ + 1/(2cosβ))/dβ.

к нулю, получаем cos²β = 1/2. Таким образом, минимальный угол, который дает минимум начальной скорости, равен 45°.    Имеется и другой метод, который использует неравенство между средним арифметическим и средним геометрическим. В нашем случае можно записать

(1/2)(cosβ + 1/(2cosβ)) ≥ √{cosβ/(2cosβ)} = √2/2,

так что минимальное значение суммы cosβ + 1/(2cosβ) равно √2, откуда следует, что β = 45°.    Это и есть угол, под которым тело касается цилиндра при полете в оптимальном случае. Если допустить β = 0 (точка E), то потребуется большая начальная скорость, так как cosβ + 1/(2cosβ) = 1,5 > √2. Из этого следует, что траектория с минимальной начальной скоростью не касается ствола в его самой высокой точке (точка E). Гравитационная потенциальная энергия тела больше на пике параболы, чем в высшей точке цилиндра, но его кинетическая энергия и полная энергия меньше, чем они были бы для траектории, касающейся вершины.    Таким образом, минимальная начальная скорость тела равна

v_1min = √{2gR(1 + √2)} = √{4,83gR}.

   Примечания.    а) Можно показать, что часть параболической траектории над точкой B не пересекает цилиндр.    б) Довольно легко определить также угол начального броска и расстояния AD. Расчеты дают

α ≥ 3π/8 = 67,5°, AD = R(1 + √2/2).

   в) Обратите внимание на то, что точка F является фокусом параболы.    г) Минимальная скорость тела, если оно, перелетая цилиндр, все же касается в верхней точке траектории вершины может быть найдена из следующих соображений.    Воспользуемся законом сохранения энергии для точки E

mv₁²/2 = mv_x²/2 + mg2R.

   Нормальное ускорение тела в верхней точке траектории

a_n = v_x²/R₁ = gcosα₁,

где α₁ − угол между вектором скорости тела в точке траектории и горизонталью, радиус кривизны в данной точке. Для верхней точки

α₁ = 0 и R₁ = R, тогда v_x² = gR.

   Сделаем подстановку в закон сохранения для верхней точки

v₁² = 5gR и v₁ = √{5gR}.

   Как видим v₁ > v _1min.

  Открытый сверху вагон, катящийся по рельсам без трения, заезжает на загрузку песка. Начальная скорость вагона v_o, масса пустого вагона m_o, масса загруженного песка m₁. Подача песка осуществляется равномерно так, что оно покрывает пол вагона слоем постоянной высоты. Найдите время загрузки Т вагона.    Примечание: форма вагона представляет собой параллелепипед.

   Решение:    Введем одномерную систему координат Ox, совпадающей с рельсом (любым). Начало координат – передняя часть вагона перед началом засыпания песка; направление – вдоль скорости вагона. Координата x – положение передней стенки вагона (x_o = 0).

   Координата x меняется со временем, когда весь вагон загрузится песком (через время T), она будет равна длине вагона: x(T) = L.    Так же, как видно из рисунка, такое положение начала координат позволяет заявить, что длина насыпанной части песка в момент времени t равна x(t).    Основа решения: закон сохранения импульса. Рассмотрим его проекцию на ось Ox (здесь не будем учитывать импульс падающего песка):

m_ov_o = const = m(t)v(t).

   Так как масса с насыпанием песка увеличивается, то скорость вагона уменьшается.    Рассмотрим момент времени t (начало отсчета времени – начало засыпания песка). Найдем массу песка:

m_n = ρV = ρbhx, m_n(t) = ρbh × x(t),

где ρ – плотность песка, b – толщина вагона, h – высота слоя песка, x – координата.    Мы знаем, что

m_n(T) = m₁; x(t) = L; m₁ = ρbhL,

отсюда

ρbh = (m₁/L),

и

m_n(t) = (m₁/L) × x(t).

   Вернемся к закону сохранения импульса:

m_ov_o = m(t)v(t) = {(m₁/L)x(t) + m_o}v(t), m_ov_o = m(t)v(t) = {(m₁/L)x(t) + m_o}x^/(t). (1)

   Получили дифференциальное уравнение, но решить его несложно, можно даже до конца его не решать. Перепишем (1) в другом виде:

m_ov_o = {(m₁/L)x(t) + m_o}dx/dt,

или

m_ov_o = {(m₁/L)x(t)dx/dt + m_odx/dt

и

m_ov_odt = {(m₁/L)x(t)dx + m_odx.

   Проинтегрируем от начала отсчета времени (начало координат) до времени t (когда координата x):

₀∫^tm_ov_odt = ₀∫^x(m₁/L)dx + ₀∫^xm_odx,

m_ov_ot = (m₁/L)x²/2 + m_ox.

Получаем:

m_ox(t) +[m₁/(2L)]x²(t) = m_ov_ot.

   В принципе, отсюда, решая квадратное уравнение можно получить функцию x(t), но нам для решения это не понадобиться. Зная, что x(T) = L, найдем T:

m_oL + m₁/(2L) × L² = m_ov_oT,

   Откуда

T = (m_o + m₁/2)L/(m_ov_o).

• Следующая задача

С поверхности бесконечной пластины с начальной скоростью v_o, направленной перпендикулярно пластине, вылетает электрон. Определите, на какое максимальное расстояние от пластины удалится электрон, если    а) над пластиной создано однородное электрическое поле, напряженности E, направленной перпендикулярно пластине;    б) над пластиной создано однородное магнитное поле, индукции B, направленной параллельно пластине;    в) над пластиной созданы однородное электрическое поле, напряженности E, направленной перпендикулярно пластине, и однородное магнитное поле, индукции B, направленной параллельно пластине.

   Решение:    1) По мере удаления электрона от пластины возрастает его потенциальная энергия в электростатическом поле пластины.

В точке максимального подъема кинетическая энергия (и скорость) обратится в нуль. По закону сохранения энергии

mv_o²/2 + 0 = 0 + eEh₁,

где m_o – масса электрона, e – его заряд. Тогда

h₁ = m_ov_o²/(2eE).

   2) В магнитном поле на заряд будет действовать сила Лоренца, вследствие которой он будет двигаться по дуге окружности (пролетит пол-окружности и ударится о плоскость).

   По второму закону Ньютона:

m_ov_o²/R = ev_oB

и

R = m_ov_o/(eB).

Из рисунка ясно, что максимальное расстояние от электрона до пластины – радиус окружности:

h₂ = R = m_ov_o/(eB).

   3) Рассмотрим электрон в некоторой точке A (рис.),

его скорость v_n. На него действуют силы: F_k = Ee и F_L = e(v_n × B) (векторное произведение) . На ось Ox может иметь только проекцию только F_L.    Запишем второй закон Ньютона для этой проекции:    Ox: m_oa_x = F_Lcosα = ev_nBcosα, но v_ncosα = v_nsin(90° − α) = v_ny – проекция скорости на ось Y.    Получаем: m_oa_x = eBv_ny, вспомним смысл ускорения и скорости:

m_odv_x/dt = eBdy/dt, m_odv_x = eBdy.

   Взяв за начало координат точку запуска электрона, и с учетом того, что в начале движения v_x = 0, проинтегрируем:

₀∫^v_xm_odv_x = ₀∫^yeBdy, m_ov_x = eBy. (1)

   В процессе полета электрона, F_k и F_L только уменьшают его проекцию скорости на ось Oy (v_y) (F_k всегда направлена вниз, а F_Lповорачивает ее, тем самым уменьшая проекцию). Можно утверждать, что в точке максимального удаления от пластины v_y = 0(дальше будет становиться отрицательной и электрон начнет приближаться к пластине). Поэтому в точке максимального удаления v = v_x, и уравнение (1) для этой точки:

m_ov = eBh₃, v = eBh₃/m_o.

   Закон сохранения энергии в момент вылета и в точке максимального подъема:

m_ov_o²/2 + 0 = m_ov²/2 + eEh₃,

m_ov_o²/2 = m_oe²B²h₃²/(2m_o²) + eEh₃,

выразим h₃:

h₃² × e²B²/(2m_o) + h₃eE − m_ov_o²/2 = 0,

h₃ = [−m_oE ± m_o√{E² + B²v_o²}]/(eB²),

h₃ ≥ 0, поэтому один корень отбрасываем:

h₃ = (m_o/(eB²)) × (√{E² + B²v_o²} − E).

• Следующая задача

  На корабле, отплывающем от крутого берега, время от времени измеряют глубину моря. На расстоянии L₁ = 100 м от берега глубина моря оказалась h₁ = 150 м, на удалении L₂ = 140 м зафиксирована глубина h₂ = 200 м, на расстоянии L₃ = 210 м от берега эхолот зарегистрировал два отражённых сигнала. Один из них соответствует глубине h₃ = 300 м, а другой h₄ = 400 м. Было высказано предположение, что второй сигнал обусловлен изменением знака наклона морского дна. Исходя из этого предположения, определите каков угол подъёма морского дна далее по курсу корабля.    При измерении глубины с корабля посылается направленная акустическая волна вертикально вниз. При взаимодействии со дном волна изотропно отражается во все стороны. На корабле регистрируется отражённый сигнал. При решении задачи могут понадобиться некоторые свойства эллипса. Напомним их. Сумма расстояний от любой точки эллипса до его фокусов − постоянная величина, равная длине его большей оси. Малая полуось эллипса b = √{a² − c²}, где a − большая полуось, а c − расстояние от фокусов эллипса до его центра. Уравнение эллипса имеет вид:

x²/a² + y²/b² = 1,

где начало декартовой системы координат расположено в центре эллипса, ось x направлена вдоль большой оси, а y − вдоль малой. Нормаль к эллипсу в точке является биссектрисой угла между прямыми, соединяющими эту точку с фокусами эллипса.

• Следующая задача

 Снег, лежащий на склоне гор, иногда приходит в движение, образуя снежные лавины. Снежные массы неожиданно начинают спускаться сверху, увлекая за собой всё, что находится на склоне горы. Энергия лавины быстро нарастает, превращая её в грозное стихийное бедствие. Для описания движения лавины воспользуемся следующей моделью.

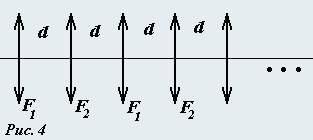
   На длинной наклонной плоскости с углом α через одинаковые промежутки L расставлены тяжёлые бруски (рис.). От скольжения по плоскости их удерживают сила сцепления, которая исчезает при сколь угодно малом толчке. После освобождения бруски скользят с ничтожным трением. Если верхний брусок придёт в движение, он столкнётся со вторым бруском, далее цепочка из двух брусков столкнётся с третьим и так далее. Все соударения предполагаются абсолютно неупругими. В результате возникает длинная цепочка, к которой присоединяются всё новые и новые бруски. Этот процесс и моделирует движение лавины по горному склону.

1. Пусть в цепочке движется n брусков. Определите приращение кинетической энергии ΔE цепочки после столкновения с (n + 1)−м бруском по сравнению с энергией после столкновения с n-м бруском.

2. Найдите разность энергий цепочек из n>> 1 и k > n брусков E_k − E_n.

3. Как сказывается на движении лавины учёт силы трения? Ответьте на вопросы предыдущих заданий, полагая, что угол наклона плоскости α больше «лавиноопасного» угла β.

• Следующая задача

  Одним из важных и обширных приложений классической механики является небесная механика, описывающая движение космических объектов.    В данной задаче речь идёт о движении двух планет Солнечной системы − Земли и Марса. Период обращения Земли вокруг Солнца равен T_E = 365 суток, а марсианский год составляет T_M = kT_E, где k = 1,88. В отдельные моменты времени планеты оказываются в положении, которое называют противостоянием. При противостоянии Марс виден с Земли в направлении, противоположном Солнцу. При этом он совершает так называемое «попятное движение», то есть вблизи точек противостояния меняет на противоположное направление своего движения относительно звёзд.    1. На рисунке показано положение Земли E, Марса M и Солнца S в противостоянии. Предполагая, что движение планет происходит по концентрическим окружностям вокруг Солнца, определите радиус R_М орбиты Марса, а также промежуток времени τ между двумя последовательными противостояниями, полагая известным радиус земной орбиты R_E = 1,50 × 10¹¹ м.

   2. Считая, что планеты движутся по часовой стрелке (рис.), найдите, на какой угол φ повернётся линия противостояния за времяτ.    3. Наблюдения показывают, что промежутки времени между последовательными противостояниями не одинаковы. Указанные промежутки плавно изменяются от значения τ_min = 764 суток до τ_max = 811 суток. Можно предположить, что это обусловлено отличием орбиты Марса от окружности. Считая, что движение Марса происходит по эллипсу, покажите, что промежуток времени между последовательными противостояниями вблизи перигелия (ближайшей к Солнцу точки орбиты) наибольший, а вблизи афелия (наиболее удалённой от Солнца точки орбиты) − наименьший. Найдите минимальное R_min и максимальное R_max удаление Марса от Солнца.

• Следующая задача

   Для определения масс ионов используют масс-спектрографы. В школьном курсе физики вы познакомились с приборами, в которых пространственное разделение ионов различных масс происходит в постоянном магнитном поле. Возможны и другие физические принципы разделения ионов. Так, в динамических масс-спектрографах селекция ионов происходит благодаря различию скоростей движения ионов в электрическом поле.    Часть 1. Постоянное поле.    Предлагаем рассмотреть простейший динамический масс-спектрометр, схема которого изображена на рисунке.

   Однозарядные ионы вылетают из источника ионов И с пренебрежимо малой скоростью, затем попадают в область ускоряющего электрического поля 1, ширина которой равна S. В этой области электрическое поле создается постоянным напряжением U, приложенным к пластине П1, расположенной непосредственно у источника, и сетке С1. Ускорившиеся ионы, свободно пролетают через сетку, и, пройдя эквипотенциальный промежуток длиной L, попадают на коллектор (устройство, собирающее ионы), подключенный к прибору, регистрирующему силу ионного тока в зависимости от времени. Источник и регистрирующее устройство включают в момент времени t = 0. Источник является импульсным, то есть ионы испускаются в течение малого промежутка времениτ, плотность потока ионов в этом временном промежутке можно считать постоянной.    1.1 Пусть источник испускает одинаковые ионы массой m. Постройте график зависимости регистрируемого ионного тока от времени.    1.2 Пусть источник испускает ионы двух типов, массы которых отличаются незначительно и равны m и m + δm, причем δm << m. Присутствие ионов двух типов проявляется в виде двух импульсов на графике I(t). Ионы различных типов называются разрешёнными, если соответствующие им импульсы ионного тока не перекрываются во времени. Покажите, что минимальная разность масс ионов, которые разрешаются рассматриваемым прибором, удовлетворяет условию δm = α√m.    1.3 Получите формулу, связывающую коэффициент α с параметрами прибора.    Рассчитайте численное значение этого коэффициента при τ = 1,0 × 10⁻⁶ c, S = 0,30 м, L = 2,0 м, U = 200 B и для массы ионов, измеряемой в а.е.м. (атомных единицах массы).    1.4 Сможет ли масс-спектрометр с такими параметрами разрешить ионы ⁵⁴Fe⁺ и ⁵⁶Fe⁺ Заряд электрона e = 1,6 × 10⁻¹⁹ Кл, постоянная Авогадро N_A = 6,02 × 10²³ 1/моль.

   Часть 2. Высокочастотное поле.    Рассмотренный выше масс-спектрометр обладает рядом недостатков: во-первых, достаточно большие размеры, во-вторых, высокие требования к источнику ионов. Существуют более компактные масс-спектрометры, не требующие импульсных источников ионов. Рассмотрим, так называемый, радиочастотный масс-спектрометр, схематически изображённый на рисунке.

   Источник однозарядных ионов работает непрерывно и скорость ионов на его выходе практически равна нулю. Поток ионов проходит через ряд сеток, между которыми создаются электрические поля различных типов. После их прохождения ионы собираются коллектором К, соединенным с измерителем ионного тока. К сеткам, ограничивающим промежуток 1, прикладывается постоянная разность потенциалов U_o = 1,0 кВ, создающая поле, ускоряющее ионы. Это же напряжение прикладывается к сеткам, ограничивающим промежуток 3, в котором оно создает постоянное тормозящее электрическое поле. В промежутке 2, ширина которого h, создается высокочастотное электрическое поле. К границам этого промежутка прикладывается переменное напряжение, циклическая частота которого ω может изменяться в пределах (5 ÷ 15) × 10⁶ c⁻¹. Амплитудное значение этого напряжения равноU₁ = 1,0 B. Наконец, к промежутку 4 прикладывается регулируемая задерживающая разность потенциалов U_з, величина которой близка к амплитудному значению напряжения высокочастотного поля.    Прибор регистрирует значение ионного тока, усредненное по промежутку времени, значительно превышающему период изменения высокочастотного поля.    Ионы, ускорившиеся в промежутке 1, попадают в область высокочастотного поля в различные моменты времени. Изменение энергии ионов в области высокочастотного поля зависит от типа ионов и момента попадания в рассматриваемую область. При некоторых условиях приращение энергии этих ионов может быть достаточным для того, чтобы преодолеть области задерживающих полей 3 и 4. Эти ионы попадут на коллектор и создадут регистрируемый ионный ток. Зависимость среднего ионного тока от частоты переменного поля в промежутке 2 может иметь ряд достаточно резких максимумов, положение которых зависит от масс исследуемых ионов. Тем самым существует возможность различать ионы различных типов. В данной части вам предлагается проанализировать работу этого прибора.

   2.1 Определите скорость v₁ иона массы m после прохождения ускоряющего напряжения в промежутке 1 и максимальное ускорениеa₁ этого иона в промежутке 2. Найдите численное значение v₁ для иона ⁵⁶Fe⁺.    2.2 Оцените по порядку величины ширину промежутка 2, при которой указанный ион, влетев в промежуток в удачный момент времени, максимально увеличит свою энергию в высокочастотном поле при его частоте ω = 10 × 10² c⁻¹.    Совместим начало отсчета оси координат Ox с началом области высокочастотного поля.    2.3 Пусть ион массы m, прошедший ускоряющий промежуток 1, попадает на левую сетку промежутка 2 в момент времени τ, при котором разность потенциалов в промежутке 2 U = U₁sinωτ. Найдите зависимость ускорения, скорости и координаты иона от времени a(t), v(t), x(t), где t отсчитывается от момента попадания иона в промежуток 2.    2.4 Из-за малости U₁, изменение скорости иона в промежутке 2 незначительно, поэтому, при расчете времени пролета этого промежутка, изменением скорости иона можно пренебречь. Определите время t₁ пролёта этого промежутка для иона массы m, используя это приближение. Оцените относительную погрешность полученного выражения.    2.5 При заданной ширине промежутка высокочастотного поля h, изменение энергии ΔE ионов массы m, при его пролёте, зависит от частоты переменного поля ω и момента времени прихода τ.    Установите зависимость изменения энергии иона в этой области от указанных величин ΔE(ω, τ).    Воспользуйтесь формулой:

cosα − cosβ = −2sin[(α + β)/2]sin[(α − β)/2].

   2.6 Так как источник ионов работает непрерывно, то ионы попадают в область высокочастотного поля в произвольные моменты времени τ. Некоторые из них, попадающие в эту область в оптимальные моменты времени (которые, возможно зависят от частоты поля), приобретают максимальную энергию (при заданном значении частоты поля ω) ΔE(ω). Для анализа зависимости изменения энергии от параметров установки и типа ионов удобно представить зависимость ΔE_max от безразмерного параметра φ = ωh/v_o − изменение фазы высокочастотного поля за время пролета иона. Постройте примерный график зависимости ΔE_max от указанного параметра.    Полученная вами функция, скорее всего, имеет множество экстремумов в зависимости от φ, многие из которых пригодны для анализа состава потока ионов. Если частота переменного поля такова, что ионы определенной массы m, приобретают дополнительную энергию большую, чем ионы других близких масс, то, изменяя задерживающее напряжение, существует возможность выделить из всего потока ионов только ионы данной массы m. В этом случае только эти ионы будут создавать ионный ток. Ионы другой массы будут достигать коллектора при другой частоте переменного поля. Таким образом, в зависимости ионного тока от частоты поля будут наблюдаться максимумы, каждый из которых соответствует ионам определенной массы.    2.7 Укажите на графике значение параметра φ_o, вблизи которого рассматриваемый прибор способен анализировать состав ионного потока наиболее эффективно.    Пусть источник испускает одинаковые ионы массы m. Ширина промежутка h.    2.8 Определите частоту поля ω_o, при которой приращение энергии этих ионов будет максимально в указанной оптимальной области работы прибора. Найдите это максимальное приращение энергии ΔE_max и значение времени прихода ионов τ_o, при котором оно реализуется.    2.9 Пусть частота поля равна найденной частоте ω_o. Чему должно быть равно максимальное значение запирающего напряженияU_з0, при котором ионный ток становится равным нулю. Представьте это значение в виде U_з0 = αU₁, рассчитайте численное значение коэффициента α с точностью до трех значащих цифр.    2.10 Для регистрации тока запирающее напряжение нужно немного уменьшить. Пусть U_з = U_з0(1 − η), где η > > 1. Найдите зависимость ионного тока от величины η. Сила тока, создаваемая рассматриваемыми ионами массы m, на выходе источника равна I_o.    2.11 При заданной величине η можно регистрировать ток даже в том случае, если частота ω отличается от ω_o на некоторую малую величину Δω. Найдите максимальное значение этой величины.    2.12 Пусть источник испускает ионы двух близких масс m и m + δm. При заданном η определите при каком минимальном отношении δm/m эти ионы ещё могут быть разрешены.

• Следующая задача

  В данной задаче рассматривается достаточно простая модель, демонстрирующая принципы работы оптического квантового генератора.    Согласно квантовой теории атомы и молекулы могут находиться в дискретном наборе состояний, энергии которых имеют строго определенные значения. Невозбужденные молекулы находятся в основном состоянии с минимально возможным значением энергии. При поглощении кванта света, энергия которого равна разности энергий возбужденного и основного состояний, молекула переходит в возбужденное состояние. Поглощательная способность молекулы характеризуется так называемым сечением поглощения σ.

   Часть 1. Поглощение и испускание.    1.1 Пусть световой поток малой плотности I_o (число фотонов пересекающих площадку единичной площади в единицу времени) падает на тонкий слой вещества толщиной Δx, концентрация поглощающих молекул в котором равна γ, причем среднее расстояние между молекулами значительно превышает их размеры.

Определите плотность светового потока I на выходе из этого слоя. Относительное изменение плотности потока p = I/I_o при прохождении поглощающего слоя назовем коэффициентом пропускания.    Поглощающие молекулы можно представить в виде шариков с площадью поперечного сечения равной сечению поглощения σ.

   1.2 Теперь будем считать, что толщина слоя очень велика. Оцените среднюю длину пробега фотонов в этом веществе.    1.3 Если молекула находится в возбужденном состоянии, то она самопроизвольно переходит в основное состояние с испусканием кванта света. Этот процесс является случайным, подобным радиоактивному распаду. Если число возбужденных молекул равно N_o, то за малый промежуток времени Δt в основное состояние перейдут ΔN = AN_oΔt молекул, где A − постоянный коэффициент, называемый коэффициентом Эйнштейна для спонтанного испускания. Оцените среднее время жизни молекулы в возбужденном состоянии.    1.4 Если молекула находится в возбужденном состоянии, то при ее взаимодействии с квантом света, энергия которого равна разности энергий возбужденного и основного состояний, молекула может испустить квант света, аналогичный исходному. Этот процесс называется вынужденным испусканием. Для такого процесса также определяется сечение вынужденного испускания σ₁. При переходах молекулы между одной и той же парой энергетических уровней сечения поглощения (переход «вверх») и сечение вынужденного испускания (переход «вниз») равны. Определите зависимость пропускания слоя, описанного в пункте 1.1, от плотности падающего потока.

   Часть 2. Резонатор.    2.1 Оптический резонатор образован двумя плоскими зеркалами, направленными друг на друга и расположенными на расстоянии Lдруг от друга. Одно зеркало является идеальным, то есть его коэффициент отражения равен 1. Коэффициент отражения второго зеркала незначительно меньше единицы и равен ρ, поэтому часть излучения выходит из резонатора. Поглощением излучения внутри резонатора и в зеркалах можно пренебречь.

Пусть поток фотонов распространяется внутри резонатора параллельно его оси. Оцените время жизни фотона в резонаторе.

   Часть 3. Лазер.    Резонатор, описанный выше, полностью заполнен веществом − раствором, содержащим активные молекулы, концентрация которых равна γ. Раствор непрерывно освещается сбоку световым потоком плотности I_o (плотность накачки).

   Частота этого излучения такова, что под его действием молекулы вещества переходят из основного (0) в возбужденное состояние(1). Сечение поглощения молекул при этом переходе равно σ_o. Далее молекулы практически мгновенно переходят в промежуточное состояние (2). Коэффициент Эйнштейна для спонтанного перехода из этого состояния во все нижележащие равен A. При определенных условия возможна генерация излучения, благодаря вынужденным переходам молекул из состояния (2) в промежуточное состояние (3). Сечение испускания этого перехода равно σ₁. Из промежуточного состояния (3) молекула практически мгновенно переходит в основное состояние (0). Генерируемый поток распространяется вдоль оси резонатора. Так как переходы с поглощение и испусканием происходят между различными парами уровней, то излучение накачки не поглощается и не вызывает вынужденного испускания в канале (3) − (2), а излучение генерации не поглощается и не вызывает вынужденного испускания в канале (0) − (1). Концентрация активных молекул достаточно мала, так что длины пробегов фотонов заметно превышают размеры резонатора.

   3.1 Определите минимальную плотность потока накачки (пороговое значение), при которой возможна генерация излучения.    3.2 Найдите зависимость интенсивности генерированного излучения лазера после выхода из резонатора, постройте схематический график этой зависимости.

• Следующая задача

1. На поверхность воды падает γ-излучение с длиной волны λ = 0,414 пм. На какой глубине интенсивность излучения уменьшится в 2 раза? [решение]

 2. Однородный шар скатывается без скольжения с плоскости, наклоненной под углом α к горизонту. За какое время он пройдет путь l и какой будет его скорость в конце пути? [решение]

 3. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам x₁ = acosωt, x₂ = acos2ωt. Найти максимальную скорость точки. [решение]

 4. Найти период малых вертикальных колебаний шарика массы m = 40 г, укрепленного на середине горизонтально натянутой струны длины l = 1,0 м. Натяжение струны считать постоянным и равным F = 20 Н. [решение]

 5. Колебания обычного математического маятника изохронны (точнее, приблизительно изохронны) только тогда, когда их амплитуды малы. Гюйгенс задался целью построить маятник, который совершал бы строго изохронные колебания при любых амплитудах. Он показал, что таковым является циклоидальный маятник. Циклоидальный математический маятник представляет собой материальную точку, совершающую колебания, двигаясь под действием силы тяжести по дуге циклоиды. Показать, что колебания циклоидального маятника изохронны, и вывести формулу для его периода. [решение]

 6. Однородный тонкий стержень массой М и длиной L висит на шарнире без трения. В нижней своей части, как показано на рисунке, он связан со стеной посредством пружины, обладающей жесткостью k. Чему равен период колебаний стержня? [решение]

 7. Камень дважды бросают с одной и той же по модулю скоростью. Первый раз на максимальную высоту H = 90 м. Найти в градусах угол, под которым брошен камень во второй раз, если его скорость в верхней точке траектории равна 15 м/с. [решение]

  1(РГУНГ 2002). Автомобиль, двигаясь равноускоренно, через 4 с после начала движения достиг скорости 8 м/с. Какой путь прошел автомобиль за четвертую секунду движения? [решение]

   2(РГУНГ 2002). Камень, брошенный под углом к горизонту, достиг наибольшей высоты 5 м. Найдите полное время полета камня. [решение]

   3(РГУНГ 2003). Из окна, расположенного на высоте 20 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень? [решение]

   4(РГУНГ 2003). За четвертую секунду равноускоренного движения тело проходит путь 4 м и останавливается. Какой путь оно прошло за вторую секунду? [решение]

   5(РГУНГ 2003). С высоты 12 м брошен мяч вертикально вверх со скоростью 2 м/с. На какой высоте окажется мяч через 1 с? [решение]

   6(РГУНГ 2004). Из некоторой точки горы с углом наклона к горизонту 30° бросают горизонтально мяч с начальной скоростью 30 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости упадет мяч? [решение]

   7(РГУНГ 2005). За две секунды движения тело прошло путь 20 м, при этом его скорость, не меняя направления, увеличилась в 3 раза по сравнению с первоначальной. Каково было ускорение тела? [решение]

   8(РГУНГ 2005). Мяч брошен с некоторой высоты вертикально вниз со скоростью 4,5 м/с. Найдите среднюю скорость движения мяча за первые пять секунд движения. Ускорение свободного падения 9,8 м/с². [решение]

   9(РГУНГ 2006). Тело брошено горизонтально. Через 3 с после броска угол между направлением полной скорости и направлением полного ускорения стал равным 60°. Определите величину полной скорости тела в этот момент времени. [решение]

   10(РГУНГ 2006). Из одной точки одновременно бросают два тела: одно горизонтально со скоростью 6 м/с, а другое – вертикально со скоростью 8 м/с. На каком расстоянии друг от друга будут находиться тела через 2 c? [решение]

   11(РГУНГ 2007). Камень, брошенный под углом к горизонту, находился в полете 4 с. Какой наибольшей высоты достиг камень? [решение]

   12(РГУНГ 2007). Автомобиль, двигаясь равноускоренно, через 4 с после начала движения достиг скорости 8 м/с. Какой путь прошел автомобиль за четыре секунды движения? [решение]

   13(МГИЭТ 2002). Легковой автомобиль движется прямолинейно со скоростью v₁ = 72 км/ч за грузовиком, скорость которого v₂= 54 км/ч. Когда расстояние между автомобилями составило L = 15 м, легковой автомобиль начал тормозить с ускорением a = 2,5 м/с² и остановился. Найдите минимальное расстояние L_min между автомобилями при их движении. [решение]

   14(МГИЭТ 2002). Две шестерни с радиусами R₁ = 8 см и R₂ =3 см находятся в зацеплении друг с другом (рис.). Большая из них вращается с угловой скоростью w₁ = 20 рад/с. а) Найдите угловую скорость w₂ второй шестерни. б) В некоторый момент времени метки A и B, поставленные на шестернях, совпадают. Определите минимальное время t, через которое метки опять совпадут. [решение]

   15(НГУ).Какое расстояние |AB| пролетит мячик, брошенный под углом α к горизонтальной плоскости со скоростью v, если он ударился о потолок? Высота потолка H, удар упругий, трения нет. [решение]

   16(МГИЭТ 2004). Два камня брошены из одной точки под различными углами к горизонту со скоростями v₁ и v₂, как показано на рисунке. Во сколько раз отличаются горизонтальные дальности их полета? Сопротивлением воздуха пренебречь. [решение]

   17(Ш). Самолет летит горизонтально на высоте H со сверхзвуковой скоростью. Наблюдатель на Земле услышал звук двигателя самолета через время Δt после того, как самолет оказался над ним. Определить скорость самолета v_с, если скорость звука в воздухеv_з. [решение]

   18(Ш). С подводной лодки, погружающейся вертикально и равномерно, испускаются звуковые импульсы длительности τ_o. Длительность приема отраженного от дна импульса τ. Скорость звука в воде c. С какой скоростью погружается подводная лодка? [решение]

   19(Ш).Первую треть пути велосипедист ехал со скоростью 20 км/ч. Средняя скорость велосипедиста на всём пути равна 25 км/ч. С какой скоростью он ехал оставшуюся часть пути? [решение]

   20(Ш). Точка движется в плоскости, причем ее прямоугольные координаты определяются уравнениями x = Acosωt, y = Asinωt, где A и ω – постоянные. Какова форма траектории точки? [решение]

21(Ш). Найдите радиус вращающегося колеса, если линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на l = 3 см ближе к оси колеса. [решение]

 22(Ш).Спортсмен пробегает 100 м за 10 с. Первые 10 м после старта он бежит с постоянным ускорением, остальную часть дистанции с постоянной скоростью. Найти ускорение на первых 10 м и скорость на остальной дистанции. [решение]

 23(А). Кошка бежит за мышкой по окружности радиусом 5 м постоянной скоростью 40 км/ч. Когда расстояние по дуге между ними было равно 1/8 длины окружности, мышка начала убегать со скоростью 50 км/ч. Через какое время мышка удалится от кошки на расстояние, равное половине окружности? [решение]

 24. Два тела начинают одновременно двигаться из начала координат вдоль оси OX. Зависимость проекций скоростей тел от времени представлена на рисунке.

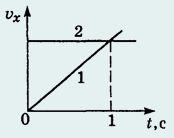
Тела встретятся в момент времени t, равный: 1) 1 с; 2) 2 c; 3) 3 c; 4) 4 c; 5) c. [ решение]

 25(Т). Тело брошено с высоты 20 м с горизонтальной скоростью 10 м/с. Перемещение тела за одну секунду равно … м. [решение]

 26(МГУ). Покоившееся тело падает с высоты H, проходя в последнюю секунду падения третью часть пути. Определить H. Сопротивлением воздуха пренебречь. Ускорение свободного падения принять равным 10 м/с². [решение]

 27. С высоты H = 30 м свободно падает стальной шарик. При падении он сталкивается с неподвижной плитой, плоскость которой наклонена под углом 30° к горизонту, и взлетает на высоту h = 15 м над поверхностью Земли. Каково время падения шарика до удара о плиту? Удар шарика считать абсолютно упругим. [решение]

 28. С катера, движущегося по течению реки, упал круг. Через 15 минут после этого катер повернул обратно. Через какое время он снова поравняется с кругом? [решение]

  1(РГУНГ 2002). Тело поднимают вверх вдоль наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой вдвое больше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, ее длина 5 м. Найдите ускорение тела, если коэффициент трения равен 0,2. [решение]

   2(РГУНГ 2005). В лифте, поднимающемся с ускорением 1,4 м/с², на пружине жесткостью 700 Н/м висит груз массой 0,5 кг. Чему равно (в мм) удлинение пружины? Ускорение свободного падения 9,8 м/с². [решение]

   3(РГУНГ 2004). Невесомый стержень вращается в горизонтальной плоскости с угловой скоростью 30 c⁻¹. На расстояниях 0,4 м и0,3 м от оси вращения закреплены грузы, имеющие массы 0,2 кг и 0,1 кг соответственно. Какая горизонтальная сила действует на ось вращения, если ось находится между грузами? [решение]

   4(РГУНГ 2003). Замкнутая цепочка массой 157 г надета «с натягом» на жесткий вертикальный цилиндр радиусом 5 см. Когда цилиндр раскрутили до угловой скорости 20 с⁻¹, цепочка с него соскользнула вниз. Чему равно натяжение цепочки? Коэффициент трения цепочки о цилиндр 0,1. Принять π = 3,14. [решение]

   5(РГУНГ 2006). Груз массой 3 кг подвешен к потолку лифта с помощью двух нитей, каждая из которых образует с вертикалью угол 60°. Каким будет натяжение каждой нити, если лифт будет опускаться с ускорением, направленным вниз и равным 2 м/с²? [решение]

   6(РГУНГ 2006). К невесомой нити длиной 1 м прикреплен шарик массой 200 г, который равномерно вращается в вертикальной плоскости. При какой минимальной угловой скорости вращения произойдет обрыв нити, если она выдерживает максимальную нагрузку 3,8 Н? [решение]

   7(РГУНГ 2007). Шарик, подвешенный на легкой нити к потолку, вращается по окружности, лежащей в горизонтальной плоскости, с угловой скоростью 5 рад/с. Найдите расстояние (в см) между точкой подвеса и центром окружности. [решение]

   8(РГУНГ 2007). Вверх по наклонной плоскости высотой 9 м и длиной 15 м пущена шайба. Коэффициент трения равен 0,5. Найдите ускорение шайбы. В ответе укажите абсолютную величину ускорения. [решение]

   9(РГУНГ 2006). Радиус некоторой планеты в √3 раза меньше радиуса Земли, а ускорение силы тяжести на поверхности планеты в3 раза меньше, чем на поверхности Земли. Во сколько раз масса планеты меньше массы Земли? [решение]

   10(МГИЭТ 2002). По наклонной плоскости скользит с ускорением a = 1 м/с² брусок массой m = 200 г. С какой силой F нужно прижимать брусок перпендикулярно наклонной плоскости, чтобы он начал двигаться равномерно? Коэффициент трения бруска о наклонную плоскость μ = 0,1. [решение]

   11(РГУНГ 2002). Невесомый стержень может свободно вращаться вокруг горизонтальной оси, проходящей через точку, которая делит стержень в отношении 1:2. На концах стержня закреплены одинаковые грузы массой 0,5 кг каждый. Стержень приводят в горизонтальное положение. С какой силой действует он на ось сразу после этого. Ускорение свободного падения принять равным 10 м/с². [решение]

   12(МГИЭТ 2003). К вертикальной железной стене «прилипла» намагниченная шайба. К шайбе привязали легкую нить и тянут за нее так, что нить все время остается параллельной стене. Когда нить тянут вертикально вверх, шайба начинает двигаться при минимальной силе F₁ = 1,6 Н; когда нить тянут вертикально вниз, шайба приходит в движение при F₂ = 0,6 Н. Найдите массу mшайбы. [решение]

   13(НГУ). На конце линейки длины L, лежащей на горизонтальной плоскости, находится маленький грузик. Линейку начинают поднимать за тот же конец с постоянной скоростью u, направленной вверх. Через какое время t грузик начнет соскальзывать? Коэффициент трения между грузиком и линейкой μ. [решение]

   14(МГУ). Начальный участок трассы скоростного спуска, расположенный вниз по склону горы с углом наклона α = 45° к горизонту, горнолыжник прошел, не отталкиваясь палками. Какую максимальную скорость мог развить спортсмен на этом участке, если его масса m = 70 кг? Коэффициент трения лыж о снег μ = 0,1, сила сопротивления воздуха пропорциональна квадрату скорости: F = kv², где постоянный коэффициент k = 0,9 кг/м. Ускорение свободного падения принять g = 10 м/с². [решение]

   15(МФТИ). Космонавты, высадившиеся на поверхность Марса, измерили период вращения конического маятника (небольшое тело, прикрепленное к нити и движущееся по окружности в горизонтальной плоскости с постоянной скоростью), и он оказался равным T = 3 c. Длина нити l = 1 м. Угол, составляемый нитью с вертикалью, α = 30°. Найдите по эти данным ускорение свободного падения на Марсе. [решение]

   16(РГУНГ 2002). Тело массой 1 кг вращается в вертикальной плоскости на нити длиной 2 м. Когда тело при подъеме проходит точку, расположенную на 1 м выше точки подвеса нити, она обрывается. На сколько выше точки подвеса поднимется тело, если натяжение нити перед обрывом было равно 35 Н? [решение]

   17(Ш). Вообразим, что строительная техника позволяет возводить сколь угодно высокие сооружения. Какую высоту должна иметь башня, расположенная на экваторе Земли, чтобы тело, находящееся на ее вершине, было невесомым? [решение]

   18(Ш). Шайба, скользившая по льду, остановилась через время t = 5 c после удара о клюшку на расстоянии l = 20 м от места удара. Масса шайбы m = 100 г. Определите действовавшую на шайбу силу трения. [решение]

   19(Ш). В электронно-лучевой трубке электроны с начальной горизонтальной скоростью v влетают в область электрического поля напряженности E, где на них действует вертикальная сила со стороны заряженных отклоняющих пластин. Чему равна эта сила, если электроны, попадая на экран, смещаются на расстояние Y по сравнению со случаем незаряженных пластин? Экран находится на расстоянии L, от центра области действия электрической силы. Масса электрона m. [решение]

   20(Ш). Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно T₁ и T₂, а вертикальных T₃, T₄. С каким ускорением тележка движется по горизонтальной плоскости? [решение]

  21(П). Кабина лифта массой m = 1000 кг равномерно опускается со скоростью v_o = 1,0 м/с с помощью троса, перекинутого через барабан. Когда кабина опустилась на l = 10 м, барабан заклинило. Найдите максимальную силу упругости T_max, действующую на трос вследствие внезапной остановки лифта. Длина троса в момент остановки равна l = 10 м, площадь поперечного сечения троса S = 20 см², модуль Юнга материала троса E = 2,0 × 10¹¹ Па. Ускорение свободного падения g = 10 м/с². [решение]

   22. Какой должна быть скорость мотоциклиста (в метрах в секунду), чтобы он мог ездить внутри поверхности вертикального цилиндра по горизонтальному кругу, если при движении по горизонтальной поверхности при том же коэффициенте трения и скорости18 км/ч минимальный радиус поворота составляет 4,5 м? Радиус вертикального цилиндра 8 м. [решение]

   23(T). Если допустить, что Земля движется вокруг Солнца по окружности радиуса 1,5 × 10⁸ км с периодом обращения один год, а радиус Солнца 7 × 10⁵ км, то ускорение свободного падения на поверхности Солнца равно … м/с². [решение]

   24. Кольцо, изготовленное из однородного резинового жгута длиной l, массой m и жесткостью k, вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через центр кольца, с угловой скоростью ω. Найдите радиус R вращающегося кольца. [решение]

 25(МГУ). Одина раз камень бросают со скоростью v₁ по горизонтальной поверхности льда, а второй раз − со скоростью v₂ под углом α = 45° к горизонту. В каком случае камню была сообщена большая скорость и во сколько раз, если в обоих случаях перемещение камней оказались равными? Коэффициент трения камня о лед равен μ = 0,02. Сопротивлением воздуха пренебречь и считать, что во втором случае после падения камень не перемещался. [решение]

 26(МГУ). Вверх по наклонной плоскости в направлении ее наиболее крутого подъема пущена шайба. Через некоторое время она остановилась и соскальзывает вниз. Каково отношение времени спуска шайбы t₂ ко времени ее подъема t₁, если коэффициент трения шайбы о плоскость μ = 0,07, а наклон самой плоскости к горизонту α = 60°? [решение]

   1(РГУНГ 2002). Санки передвигаются по горизонтальному участку дороги с, помощью веревки, наклоненной под углом 30° к горизонту. Сила натяжения веревки составляет 100 Н. Найдите работу силы натяжения на пути 15 м. Указание: √3 = 1,72. [решение]

   2(Ш). Тело массой m = 100 г падает свободно. Определите изменение импульса этого тела за первые две секунды падения. [решение]

   3(Ш). Плот массой m₁ свободно скользит по поверхности воды со скоростью v₁. На плот с берега прыгает человек массы m₂. Скорость человека перпендикулярна к скорости плота и равна v₂. Определить скорость v плота с человеком. Силами трения плота о воду пренебречь. [решение]

   4(Ш). Вертикально вверх произведен выстрел из пушки. Начальная скорость снаряда v_o. В точке максимального подъема снаряд разорвался на две равные по массе половины. Первая упала вблизи точки выстрела, имея скорость 2v_o. Через какое время после выстрела упадет вторая половина? Какую скорость она будет иметь в момент падения? [решение]

   5(Ш). Математический маятник, т. е. небольшой шарик на тонкой нити, массой которого можно пренебречь, первоначально находится в горизонтальном положении. Длина нити маятника l. На расстоянии l/2 под точкой подвеса расположена горизонтальная плита. На какую высоту поднимется шарик после удара о плиту. Удар упругий. [решение]

   6(Ш). Призма с массой M и с углом наклона α стоит на гладкой горизонтальной поверхности льда. На призме стоит собака, масса которой m. С какой скоростью будет двигаться призма, если собака побежит вверх со скоростью v относительно призмы? Трением пренебречь. [решение]

   7(Ш). Легкий теннисный мячик ударили ногой, и он полетел в направлении движения ноги. Какую скорость приобрел мячик, если скорость движения ноги при ударе u = 10 м/с. [решение]

   8(Ш). Через блок, перекинут шнур, на концах которого закреплены грузы массой M. На высоте h находится кольцо массой m, которое скользит без трения. Через какое время t расстояние между грузами станет h, после свободного падения кольца. [решение]

   9(Ш). Человек, имеющий массу M, прыгает под углом α к горизонту со скоростью v_o. В верхней точке траектории он бросает со скоростью v₁ вертикально вниз груз массой m. На какую общую высоту H подпрыгнул человек? [решение]

   10(Ш). Ядро, летевшее в горизонтальном направлении со скоростью 20 м/с, разорвалось на два осколка массами 10 кг и 5 кг. Скорость меньшего осколка равна 90 м/с и направлена вертикально вверх. Определить модуль и направление скорости большего осколка. [решение]

   11(Ш). Массивная плита движется с постоянной скоростью u_o в положительном направлении оси X, выбранной неподвижной системы отсчета (ось X перпендикулярна к плите). Шарик массы m движется со скоростью v_o в направлении, указанном на рисунке. Определить величину и направление скорости шарика v после удара о плиту, если удар абсолютно упругий. [решение]

   12(Ш). Из неподвижной лодки массой 140 кг под углом 30° к горизонту со скоростью 5 м/с прыгает человек массой 70 кг. На какое расстояние сместится лодка, если сила сопротивления воды 30 Н? [решение]

   13(Ш). На тросе висит небольшой ящик с песком, в котором застревает поток пуль, летящих горизонтально со скоростью v. При этом трос отклоняется на угол α от вертикали. Масса пули m много меньше массы ящика M (m << M). Сколько пуль в единицу времени попадает в ящик? [решение]

   14(Ш). Пять одинаковых по размеру шариков, центры которых лежат на одной прямой, находятся на небольшом расстоянии друг от друга. Масса каждого следующего шарика в два раза меньше массы предыдущего. В первый (самый массивный) шар попадает еще один шар, масса которого в два раза больше, чем у первого, а скорость, имеющая направление вдоль прямой, соединяющей шары, равны v_o = 10 м/с. Определите скорость последнего шара, считая соударения абсолютно упругими. [решение]

   15(Ш). Грузовик едет со скоростью 7 м/с. Мячик массой 0,25 кг, брошенный вдогонку грузовика, ударяется абсолютно упруго в его задний борт с горизонтальной скоростью 10 м/с. Определите импульс мяча сразу после удара. [решение]

   16(Ш). Ракета с начальной массой m запущена вертикально вверх. Скорость газов на срезе выходного отверстия двигателя равнаv, секундный расход топлива – μ. Найти ускорение ракеты через время t с момента запуска. [решение]

   17(Ш). Сосуд с водой движется горизонтально с постоянной скоростью под действием реактивной силы, возникающей благодаря струе воды, бьющей со скоростью v из отверстия площадью S, расположенного у дна сосуда. Масса сосуда с водой равна m. Найти коэффициент трения между сосудом и плоскостью (пренебрегая изменением массы воды). [решение]

   18(Ш). Ракета с массой M взлетает вертикально с ускорением 5g. Скорость истечения газов из сопла двигателя равна v. Найти расход горючего. [решение]

   19(Ш). Какую часть веса одно ступенчатой ракеты должен составлять вес горючего, если ракета, взлетая вертикально, должна приобрести в конце работы двигателя первую космическую скорость v_m = 7,9 км/с? Сопротивлением воздуха пренебречь. Скорость истечения газов из сопла двигателя v ≅ 3440 м/с. [решение]

   20(Ш). Автомобиль с ракетным двигателем равноускоренно движется вверх по наклонной плоскости с углом наклона α и коэффициентом трения k. Скорость газов на выходе сопла двигателя равна u, а их масса, отбрасываемая за 1 c, равна μ. Скорость автомобиля в начале подъема равна v_o. Найти время, за которое автомобиль увеличил скорость от v_o до v. [решение]

21(O). Гладкая однородная веревка длины l и массы m переброшена через небольшой блок так, что вначале находится в равновесии. Веревку немного смещают, и она начинает соскальзывать с блока. С какой силой действует она на блок в момент, когда длина веревки с одной стороны от него равна l/3? [решение]

   22(279 МГУ). На легкой нерастяжимой нити длиной L висит небольшой шарик массы m. По шарику нанесли удар в горизонтальном направлении. Известно, что пока шарик после удара двигался по дуге окружности, он поднялся на высоту h. Найти среднюю силу, действовавшую на шарик во время удара, если длительность удара t много меньше периода малых колебаний шарика. Трением пренебречь. [решение]

   23(П). Тело брошено вертикально вверх с начальной скоростью 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте h кинетическая энергия тела будет равна его потенциальной энергии. [решение]

   24(9.68). С горки высотой h = 2 м и длиной основания S = 5 м съезжают санки, которые останавливаются, пройдя горизонтально некоторый путь от основания горы. Чему равен этот путь, если коэффициент трения на всем пути μ = 0,05? [решение]

   25(10.24). Небольшое тело соскальзывает по наклонной плоскости, плавно переходящей в «мертвую петлю» радиусом 2 м. С какой минимальной высоты должно соскальзывать тело для благополучного прохождения всей петли? Высота отсчитывается от нижней точки петли. Трением пренебречь. [решение]

   26. Тонкую мягкую цепочку массой m = 200 г удерживают за один конец так, что другой ее конец касается стола. Цепочку отпускают, и она падает на стол. Считая, что все элементы цепочки находящиеся в воздухе, падают свободно, найдите силу давления на стол в том момент, когда в воздухе находится половина цепочки. [решение]

   27(T). Два шара массами m и 2m движутся по взаимно перпендикулярным направлениям с равными по величине скоростями. После соударения тело массой m останавливается. Какую часть его энергии (в %) составляет выделившаяся при ударе теплота? … %. [решение]

   28(T). Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна 200 м/с. В точке максимального подъема снаряд разорвался на два одинаковых осколка. Первый упал на землю вблизи точки выстрела со скоростью 250 м/с. Через какое время после этого упадет второй осколок? Сопротивлением воздуха пренебречь. [решение]

   29. Ракета имеет запас топлива m = 8 т. Масса ракеты (включая топливо) M = 15 т. Топливо сгорает за 40 c. Расход топлива и сила тяги F = 200000 H постоянны.    1) Ракета установлена горизонтально на тележке. Определить ускорение, которое имеет ракета в момент запуска. 2) Найти зависимость ускорения от времени движения ракеты и изобразить эту зависимость графически. 3) По графику оценить величину скорости, которую приобретает ракета через 20 c после начала движения. Трение не учитывать. [решение]

   30. Ракета запускается вертикально вверх. Измерения показали, что через 20 c ускорение ракеты равно 0,8g. Рассчитать силу сопротивления воздуха, которая действовала на ракету в этот момент. Ускорение g считать постоянным. [решение]

   31 Для измерения ускорения ракеты на ней помещен прибор, представляющий собой пружину, закрепленную в вертикальной трубке. В покое пружина растянута прикрепленным на ее конце грузом на l_o = 1 см. Определить зависимость растяжения пружины от ускорения ракеты. Что представляет собой шкала прибора? [решение]

  1(Ш). На стержень действуют две параллельные силы, равные F₁ = 10 H и F₂ = 25 Н и направленные в противоположные стороны. Определите точку приложения и величину силы, уравновешивающей силы F₁ и F₂, если их точки приложения находятся на расстоянии l = 1,5 м друг от друга. [решение]

   2(Ш). К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка висит, касаясь стенки, как показано на рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой μ = 0,1. При каком угле α между нитью и стенкой катушка висит неподвижно? [решение]

   3(Ш). В двух вершинах равностороннего треугольника помещены шарики массой m каждый. В третьей вершине находится шарик массой 2m. Найдите положение центра масс этой системы. [решение]

   4(Ш). Однородная тонкая пластинка имеет форму круга радиусом R, в котором вырезано круглое отверстие вдвое меньшего радиуса, касающегося края пластинки. Где находится ее центр тяжести? [решение]

   5(Ш). На столе лежит однородный стержень массой 6 кг так, что две трети его длины находятся за краем стола. Какую силу необходимо приложить к концу стержня для удержания его в горизонтальном положении? [решение]

   6(Ш). На абсолютно гладкой горизонтальной плоскости лежит обруч. На обруче находится жук. Какую траекторию будут описывать жук и центр обруча, если жук начнет двигаться вдоль обруча? Масса обруча M, радиус R, масса жука m. [решение]

   7(Ш). Невесомый жесткий стержень длиной l свободно лежит на двух опорах A и B. В точке C, отстоящей от A на расстоянии a, на стержень действует вертикальная нагрузка F. Найти реакцию опор. [решение]

   8(Ш). Балка весом P₁ свободно лежит на двух опорах A и B, расстояние между которыми равно l, и выступает за опору B на такую же длину l. На середине промежутка AB расположен груз P₂, а на выступающем конце – груз P₃. Найти реакции опор F_A, F_B. [решение]

   9(Ш). Куб опирается одним ребром на пол, другим – на гладкую вертикальную стенку. Определить, при каких значениях угла αвозможно равновесие куба. Коэффициент трения куба о пол равен μ, ребро куба равно a. [решение]

   10(Т). Глубина лунки в доске, в которую поставлен шар, в два раза меньше радиуса шара. При каком угле наклона доски α к горизонту шар выкатится из лунки? [решение]    1) α > 12° 2) α > 15° 3) α > 30° 4) α > 45° 5) α > 60°

   11(Т). Однородный брусок массой 720 г и длиной 120 см шарнирно закреплен на расстоянии 40 см от одного из его концов. Какую минимальную по модулю силу необходимо приложить к правому концу бруска (2), чтобы он находился в равновесии в горизонтальном положении? [решение]    1) 1,6 H 2) 2,4 H 3) 3,0 H 4) 1,8 H 5) 1,2 H

   12(Т). Использование неподвижного блока при подъеме груза обеспечивает... [решение]    1) выигрыш в силе 2) выигрыш в работе 3) выигрыш в силе и работе 4) изменение направления силы, выигрыша в силе нет 5) выигрыш в силе в 2 раза

 13(К). Какой минимальной горизонтальной силой можно опрокинуть через ребро куб, лежащий на горизонтальной плоскости? [решение]

 14(К). К цилиндрическому стержню, закрепленному сверху, в его нижнем сечении приложена сила F, направленная вдоль оси стержня (рис. а). Найти внутренние силы, возникающие в поперечных сечениях стержня. Массой стержня пренебречь. [решение]

 15(К). Определить удлинение стального ступенчатого стержня (рис. а), к которому приложены осевые силы F₁ и F₂ (|F₁| = 20 кН, |F₂| = 30 кН). Длины участков стержня равны l₁ = 1 м и l₂ = 2 м, поперечные сечения равны, соответственно, S₁ = 1 см² иS₂ = 2 см², модуль Юнга Е = 2 × 10⁵ МН/м². Стержень считать невесомым. [решение]

 16(К). Груз массы m = 2 т поддерживают два одинаковых круглых стальных стержня, соединенных шарнирно в узле А и составляющих угол α =60° с вертикалью (рис.). Определить диаметр сечения каждого стержня, если допускаемое напряжение для стали σ_доп = 160 МН/м². [решение]

   1(T). Пробирка с пластилином плавает в воде. Как изменится глубина погружения пробирки, если из нее вынуть пластилин и приклеить снаружи ко дну пробирки? [решение]    1) уменьшится 2) увеличится 3) не изменится 4) сначала придет в колебательное движение, а потом увеличится 5) после затухания колебаний не изменится.

   2(РГУНГ 2003). В цилиндрическом сосуде с водой площадью 200 см² плавает в вертикальном положении цилиндр высотой 30 сми площадью основания 100 см². Какую работу (в мДж) надо совершить, чтобы полностью извлечь цилиндр из воды, если он сделан из материала плотностью 400 кг/м³? Плотность воды 1000 кг/м³. [решение]

   3(МГУ 1996). Во сколько раз сила давления воды на нижнюю половину вертикальной стенки полностью заполненного колодца отличается от силы давления воды на всю стенку, если давление на дно колодца превышает атмосферное в n = 3 раза? [решение]

   4(МГУ 1996). В дне цистерны, заполненной нефтью, установлены два одинаковых крана K₁ и K₂ небольшого сечения, расположенных на равных расстояниях L от оси ее горловины. Считая, что скорость вытекания нефти пропорциональна перепаду давлений на кране, найти отношение масс вытекающей через краны нефти при движении цистерны по прямолинейному горизонтальному участку пути с ускорением a, если уровень нефти в центре горловины относительно дна равен h, и при движении цистерны нефть не выливается из горловины. [решение]

   5(94 НГУ). Деревянный стержень подвешен на нити над сосудом с водой. При подъеме сосуда стержень погружается в воду сначала вертикально, затем наклоняется, а при дальнейшем подъеме остается горизонтальным. Объясните демонстрируемое явление. [решение]

   6(133 МФТИ). Цилиндрическую гирю, подвешенную к динамометру, опускают в воду (рис.), пока уровень воды в сосуде не изменится на Δh = 8 см. Показание динамометра при этом изменилось на ΔF = 0,5 H. Определите сечение сосуда. [решение]

   7(Т). Уровень воды в цилиндрическом сосуде с площадью основания 5 дм² при полном погружении тела повысился на 2 см. Архимедова сила, действующая на тело, равна … H. [решение]

 8(C). Цистерну в форме куба со стороной 2 м, стоящую на платформе, заполнили водой почти доверху и закрыли. Платформа стала разгоняться с горизонтальным ускорением 2 м/с². Найдите силу давления (в кН) воды на заднюю стенку цистерны. Атмосферное давление не учитывать, g = 10 м/с². [решение]

 9(С). Открытую цистерну в форме куба со стороной 2 м, стоящую на платформе, заполнили жидкостью наполовину. Платформа стала разгоняться с ускорением 2 м/с². Насколько поднялся уровень (в см) жидкости у задней стенки платформы к тому моменту, когда жидкость и платформа стали двигаться как единое целое? g = 10 м/с². [решение]

 10(К). Батискаф представляет собой шар радиусом r = 2 м. При испытаниях в море в нижней части батискафа образовалась течь, и он затонул, а в его верхней части образовалась воздушная прослойка в виде шарового сегмента толщиной h = 1 м. Чему равна глубина моря Н, на которой затонул батискаф? Какая масса воздуха понадобится для того, чтобы вытеснить из батискафа всю воду? Начальное (атмосферное) давление воздуха в батискафе равно давлению, которое создает слой воды толщиной Н_o = 10 м.  Указание: объем шарового сегмента толщиной h равен ΔV = πh²(3r − h)/3. [решение]

 11(К). Свая в виде двух соосных цилиндров забита в грунт дна водоема глубиной H (рис.). Какая сила действует на сваю со стороны воды? Сечение верхнего цилиндра S₁, его высота h₁, сечение нижнего цилиндра S₂, высота его части, находящейся в воде, h₂. [решение]

 12(К). В стратифицированной жидкости плотность увеличивается с глубиной h no линейному закону ρ(h) = ρ(0)(1 + αh), где ρ(0) − известная плотность на поверхности. Для измерения константы α, в жидкость на нити, прикрепленной к динамометру, опускают цилиндрическое тело длиной L и сечением S. Когда тело перемещается по вертикали на Н, оставаясь целиком погруженным в жидкость, показания динамометра изменяются на ΔF. Чему равна константа α? [решение]

 13(К). В цилиндрический сосуд с площадью дна S налита вода. На сколько поднимется уровень воды, если в сосуд поместить деревянный брусок массой m? [решение]

 14(К). В цилиндрическом сосуде с площадью дна S плавает в воде кусок льда массой m_л. На сколько изменится уровень воды, если лед растает. [решение]

 15(K). В цилиндрическом сосуде площадью сечения S плавает в воде кусок льда, притянутый ко дну нитью. Когда лед растаял, уровень воды понизился на Δh. Чему была равна сила натяжения нити? [решение]

 16(К). В цилиндрическом сосуде площадью сечения S = 100 см² плавает в воде кусок льда, в который вморожен грузик из цинка массой m_ц = 35 г. На сколько понизится уровень воды, когда лед растает? Плотность цинка ρ_ц = 7000 кг/м³. [решение]

 17(К). На дне цилиндрического сосуда с водой площадью S = 300 см² стоит цилиндр высотой Н = 40 см и площадью основанияS_ц = 100 см², сделанный из материала плотностью ρ = 3000 кг/м³. Какую работу надо совершить, чтобы вытащить цилиндр из воды, если начальная толщина слоя воды h₁ = 30 см? Цилиндр поднимают в вертикальном положении. [решение]

 18(К). В цилиндрическом сосуде с водой площадью S = 300 см² плавает в вертикальном положении цилиндр высотой Н = 20 см и площадью основания S_ц = 100 см². Какую работу надо совершить, чтобы полностью извлечь цилиндр из воды, если он сделан из материала плотностью ρ = 300 кг/м³? [решение]

 19(K). В гладкий стакан высотой Н = 8 см и радиусом R = 3 см поставили однородную палочку длиной L = 12 см и массой m = 150 г. Стакан доверху наполнили жидкостью, плотность которой в 5 раз меньше плотности материала палочки. С какой силой давит палочка на край стакана? [решение]

 20. В сосуде, вертикальное сечение которого изображено на рисунке, находятся в равновесии два невесомых поршня, соединенные невесомой нерастяжимой нитью. Пространство между поршнями заполнено жидкостью, плотность которой ρ. Найти силу натяжения нити Т, если площади поршней S₁ и S₂, а длина нити l. Трением поршней о стенки сосуда пренебречь, ускорение свободного падения принять g. [решение]

1(П). Камеру объемом V = 10 л наполнили при температуре t₁ = 0 °C сухим воздухом, ввели в нее m = 3 г воды, закрыли, а затем нагрели до t₂ = 100 °C. Какое давление установится в камере, если первоначальное давление было p₁ = 10⁵ Па? [решение]

   2(П). В откачанный сосуд объемом V = 5 л поместили m = 1 г воды. Найдите давление паров воды в сосуде при температурах t₁= 20 °C и t₂ = 100 °C. Давление насыщенных паров воды при этих температурах равны соответственно p_н1 = 2,33 кПа и p_н2 = 100 кПа. [решение]

   3(НГУ 1975). В прямоугольном закрытом сосуде длиной 2l с непроницаемыми стенками находится слева тяжелая жидкость, например, ртуть, отделенная подвижным тонким поршнем от воздуха в правой части сосуда. В начальный момент поршень находится в равновесии и делит объем сосуда пополам. На сколько смещается поршень вправо, если абсолютная температура системы уменьшается в три раза? Тепловым расширением ртути и стенок сосуда, а также трением пренебречь. [решение]

   4(НГУ 1977). В запаянной с одного конца трубке сечения S находится поршень массы m на расстоянии l от запаянного конца. Другой коней трубки открыт, по обе стороны поршня – воздух с давлением p_o. Трубку начинают вращать с угловой скоростью ωвокруг вертикальной оси, проходящей через запаянный конец трубки. На каком расстоянии от дна трубки будет находиться поршень? Температура постоянна, трения нет. [решение]

   5(НГУ 1983). В центре закрытой с торцов трубы длиной 2l находится поршень массы m и площадью S, который может без трения перемещаться по трубе. Слева и справа от поршня имеется газ с давлением p. Трубу раскручивают в горизонтальной плоскости вокруг вертикальной оси, проходящей через ее центр. Найдите угловую скорость вращения, если поршень сместился на 1/2. Температуру газа считать постоянной. [решение]

   6(НГУ 1997). В вертикальном теплоизолированном сосуде под поршнем массы M необходимо подводить к нагревателю в жидкости, чтобы поршень поднимался с постоянной скоростью v? Температура внутри сосуда равна T, молярная масса μ, теплота парообразования λ. Внешнее давление отсутствует. Газовая постоянная равна R. [решение]

   7(НГУ 1999). В центре трубки с газом, запаянной с обоих концов, находится пробка, разделяющая трубку на две части длиной Lкаждая. Трубку медленно нагревают. Когда температура достигает значения T, пробка начинает перемещаться влево. При температуре 2T она сдвинется на 1/3. При какой температуре пробка окажется сдвинутой влево на расстояние 21/5? Считать, что сила трения не зависит от температуры. [решение]

   8(НГУ 2000). Цилиндрический теплоизолированный сосуд высотой 2L и площадью основания S стоит вертикально в поле тяжести (ускорение свободного падения g). Сосуд в начальный момент разделен на две одинаковые части теплопроводящим поршнем массыm, а в каждой из половинок находится газ с давлением p_o. Затем поршень отпускают, и он после затухания колебаний опускается на расстояние h от первоначального положения. Найти массу m поршня. Толщиной и теплоемкостью поршня пренебречь. Внутренняя энергия газа с давлением p и объемом V равна E = αpV, где α – некоторая константа. [решение]

   9(МИФИ 1972). В трубке, закрытой с одной стороны и закрепленной под углом α = 30° к горизонту, находится поршень массы m = 1 кг (рис.). Площадь сечения трубки S = 8 см₂. Поршень передвинули, увеличив объем воздуха под ним в n = 2 раза. Найти начальное ускорение поршня после того, как его отпустили. Трением пренебречь. Наружное давление воздуха р_o = 760 мм рт. ст. [решение]

   10(МИФИ 1980). В закрытом с обоих торцов горизонтальном цилиндре объемом V = 0,0012 м³ находится Воздух при давлении p_o= 100 кПа. Цилиндр разделен на две равные части тонким поршнем массой m = 0,1 кг. Длина цилиндра 2l = 0,4 м. Цилиндр привели во вращение с угловой скоростью ω вокруг вертикальной оси, проходящей через его середину. Найдите величину ω, если поршень оказался на расстоянии r = 0,1 м от оси вращения. [решение]

   11(РГУНГ 2007). Давление воздуха внутри плотно закупоренной бутылки при температуре 7 °С равно 150 кПа. До какой температуры (по шкале Цельсия) надо нагреть бутылку, чтобы из нее вылетела пробка, если известно, что для вынимания пробки до нагревания бутылки требовалась минимальная сила 90 Н? Площадь поперечного сечения пробки 8 см². [решение]

   12(МИФИ 1972). Внутри трубы, наполненной воздухом и закрытой с обоих торцов, может скользить без трения поршень массой m = 4 кг, плотно прилегающий к стенкам трубы. Площадь поршня S = 200 см². Определить отношение объемов воздуха в трубе по обе стороны от поршня при ее соскальзывании по наклонной плоскости, образующей с горизонтом угол α = 60°. Коэффициент трения между трубой и наклонной плоскостью k = 0,25. Известно, что в горизонтально лежащей трубе поршень занимает среднее положение, при этом, давление воздуха в трубе p = 1,25 × 10³ H/м². Температура воздуха в трубе постоянна. [решение]

   13(МИФИ 1975). В вертикальном цилиндрическом сосуде с гладкими стенками под поршнем с массой m = 10 кг и сечением S = 50 см² находится газ. При движении сосуде по вертикали с ускорением a = 1 м/с² высота столба газа под поршнем уменьшается на η = 5 % по сравнению с высотой в покоящемся сосуде. Считая температуру газа в сосуде неизменной, определите наружное давлениеp₂. Поршень герметично прилегает к стенкам сосуда, а закрытая часть его находится внизу. [решение]

   14(МИФИ 1980). В гладкой горизонтально закрепленной трубке, профиль которой показан на рисунке (см. в решении), находятся два поршня, соединенных жестким тонким стержнем. Плошали поршней S₁ = 10 см² и S₂ = 40 см². Правый поршень соединен с точкой O пружиной жесткостью k = 400 Н/м. В первоначальном состоянии температура всюду равна T_o = 300 К, давление воздуха между поршнями равно внешнему p_o = 100 кПа и пружина не деформирована. Затем газ между поршнями нагрели на ΔT = 100 K, а точку O переместили вправо на такое расстояние x, чтобы положение поршней не изменилось. Найдите х. [решение]

   15(МИФИ 1982). В цилиндре под поршнем массы М = 20 кг находится m = 1 г гелия при температуре T = 400 K (рис. смотри в решении задачи). Удлинение пружины A составляет x = 20 см, а энергия ее деформации E = 60 Дж. Определите высоту поршня над дном цилиндра. Давлением газа вне цилиндра пренебречь. [решение]

   16(МИФИ 1983). В трубке, запаянной с одного конца, находится столбик ртути длиной l = 0,3 см. Трубку вращают в горизонтальной плоскости вокруг оси, проходящей через ее закрытый конец. При какой угловой скорости вращения ртуть достигнет открытого конца, если в неподвижной горизонтальной трубке они находится на расстоянии d = 64 см от закрытого конца? Длина трубки b = 80 см. Внешнее давление p_o = 100 кПа Температура постоянна. Плотность ртути ρ = 13,6 × 10³ кг/м³. Капиллярными эффектами пренебречь. [решение]

   17(МГУ 1971). Два одинаковых баллона соединены короткой трубкой, в которой имеется клапан давления, пропускающий газ из одного баллона в другой при разности давлений Δp ≥ 80 см рт. ст. Один баллон наполнен газом, имеющим при температуре t₁ = 17 °С давление p = 760 мм рт. ст., в другом баллоне – вакуум. Какое давление установится в баллонах, если их нагреть до температуры t₂ = 109 °C? [решение]

   18(МГУ 1996). Внутри стеклянного шара радиуса r = 10 см содержится газ при давлении p₁ = 0,1 мм рт. ст. и температуре t₁ = 17 °C. При такой температуре стенки шара полностью покрыты мономолекулярным слоем адсорбированного газа. На сколько изменится давление в шаре, если его нагреть до температуры t₂ = 300 °C? Считать, что при таком нагреве все адсорбированные молекулы газа переходят со стенок в шар, а каждая адсорбированная молекула занимала поверхность S = 10⁻¹⁹ м². [решение]

   19(МГУ 1996). Идеальный газ в исходном состоянии имел температуру T_o. Затем давление газа уменьшили в n = 2 раза, увеличив его объем во столько же раз так, что объем изменялся в зависимости от давления по линейному закону. Найти максимальную температуру газа при этом процессе. [решение]

   20(МГУ 1996). В цилиндре под поршнем содержится воздух с относительной влажностью r = 80 % при температуре 100 °С и нормальном атмосферном давлении. Каким будет давление в цилиндре, если объем воздуха изотермически уменьшить в n = 2 раза? [решение]

 1(НГУ 1975). В цилиндрическом сосуде под невесомым поршнем находится насыщенный пар при температуре T. Определить, какая масса пара сконденсировалась, если при вдвигании поршня совершена работа A. Молекулярный вес пара μ, газовая постояннаяR. [решение]

 2(НГУ 1983). В теплоизолированной трубе под поршнем содержится один моль газа при давлении в два раза меньшем внешнего и температуре T. Поршень может свободно передвигаться в сторону увеличения объема и удерживается стопором от противоположного движения. Внутренняя энергия газа U = cT. газовая постоянная R. Какое количество теплоты надо подвести к газу, чтобы его объем увеличился в два раза? [решение]

 3(РГУНГ 2004). Давление идеального одноатомного газа изохорно увеличивают в 4 раза, затем объем газа увеличивают в 2,5 раза так, что давление линейно зависит от объема и возрастает в 2 раза, после чего газ возвращают в исходное состояние в процессе, в котором давление линейно зависит от объема. Найдите КПД (в процентах) такого цикла. [решение]

 4(РГУНГ 2006). В теплоизолированном цилиндре под невесомым поршнем находится идеальный одноатомный газ. Вначале поршень закреплен и соединен с дном цилиндра недеформированной пружиной. После того как поршень освободили и система пришла в равновесие, объем газа увеличился в 1,25 раза. На сколько процентов при этом уменьшилось давление? Над поршнем газа нет. [решение]

 5(НГУ 2002). Тяжелый поршень массой M может свободно перемещаться внутри вертикального теплоизолированного цилиндра сечением S, верхний торец которого закрыт, а нижний открыт в атмосферу. Внутри цилиндра имеется горизонтальная перегородка с маленьким отверстием, отсекающая от атмосферы 1 моль воздуха, который занимает объем V при атмосферном давлении p_o. Поршень, который вначале снизу к перегородке, отпускают. Полагая, что внутренняя энергия газа равна cT, найдите, насколько опустится поршень. [решение]

 6(МИФИ 1983). Пластилиновый шар бросают со скоростью v_o = 10 м/с под углом α = 60° к горизонту по направлению к вертикальной стенке, расположенной на расстоянии l = 6,3 м от точки бросания. Шар прилипает к стенке. Считая, что вся кинетическая энергия шара пошла на его нагревание, найдите приращение температуры шара. Удельная теплоемкость пластилина с = 2,5 × 103 Дж/(кг•К). [решение]

 7(МГУ 1971). Один моль азота (M = 28 г/моль) является рабочим веществом в замкнутом цикле 1 – 2 – 3 – 4 (см. рис.). Известны: p₁ =2 атм., V₁ = 10 л, T₁ = 244 К; p₂ = 4 атм., V₂ = 20 л и удельные теплоемкости c_V = 0,179 кал/(г•град) и c_p = 0,25 кал/(г•град). Какое количество тепла и на каких участках цикла поступает в систему? [решение]

 8(МГУ 1974). Цикл состоит из двух изохор и двух изобар (рис.). Температуры газа в точках 1 и 3 равны соответственно T₁ и T₂. Определить работу, совершенную одной грамм-молекулой газа за цикл, если известно, что точки 2 и 4 лежат на одной изотерме. [решение]

 9(МГУ 1996). В вертикальном цилиндре под массивным поршнем находится одноатомный газ. Сколько теплоты необходимо сообщить газу, чтобы он при расширении совершил работу ΔA? Теплообменом газа с окружающей средой пренебречь. [решение]

 10(МГУ 1996). Давление моля идеального одноатомного газа уменьшают с увеличением объема по линейному закону так, что в конечном состоянии его давление уменьшилось в n раз, а объем увеличился в k раз. Найти отношение суммарного количества переданного газу тепла к приращению его температуры при переходе газа из исходного состояния в конечное. [решение]

 11(МГУ 1996). Давление моля одноатомного газа в объеме V₁ равно p₁. Из этого состояния газ изобарически переводят в состояние 2, увеличив объем в n = 2 раза. Затем объем газа увеличивают еще в k = 1,5 раза так, что его давление уменьшается по линейному закону с ростом объема и становится в kn раз меньше p₁. Найти изменение внутренней энергии газа при переходе из состояния 2 в состояние 3. [решение]

 12(МГУ 1996). Идеальный одноатомный газ, имевший температуру T₁, изобарически переводят в состояние 2 с температурой T₂> T₁, затем изохорически – в состояние 3 с температурой T₃ < T₂, а после изобарического сжатия – в такое состояние 4, из которого его переводят в исходное состояние изохорически. Найти КПД этого цикла. [решение]

 13(МГУ 1996). Холодильник работающий по циклу Карно, поддерживает в камере температуру T_к = 260 K, отводя из нее за цикл работы энергию Q_к = 400 Дж. Температура радиатора холодильника равна T_р = 300 K. Какую среднюю мощность потребляет холодильник, если длительность его цикла равна τ = 1,5 с? [решение]

 14 (МГУ). Вертикально расположенная цилиндрическая теплоизолированная трубка диаметром d = 1 см, закрытая подвижным невесомым поршнем, содержит идеальный одноатомный газ. Внутри трубки содержится резистор с большим сопротивлением, соединенный через ключ с конденсатором емкостью С = 1 мкФ, заряженным до напряжения U = 200 В. Подводящие провода имеют ничтожно малое сопротивление и не нарушают герметичность трубки. На какое расстояние h поднимется поршень после замыкания ключа и установления теплового равновесия? Атмосферное давление р_o =10⁵ Па. [решение]

 15. Спираль, сопротивление которой r = 9 Ом, помещена в замкнутый сосуд. Сосуд содержит идеальный одноатомный газ, который занимает объем V = 6 л. В течение времени t = 1 мин по спирали пропускали постоянный ток, после чего давление возросло на величину Δр = 6 × 10⁴ Па. Найти силу тока I. [решение]

 16. Тепловая машина с максимально возможным КПД имеет в качестве нагревателя резервуар с кипящей водой при t₁ = 100 ^oС, а в качестве холодильника − сосуд со льдом при t₂ = 0 ^oС. Какая масса льда m растает при совершении машиной работы А = 10 Дж? Удельная теплота плавления льда λ = 334 Дж/г. [решение]

 17. В гладком вертикальном цилиндре под подвижным поршнем площадью S и массой M в объеме V содержится газ при температуре T. На сколько процентов увеличится температура газа, если на его нагревание затратить количество теплоты Q, атмосферное давление p_о, а теплоемкость газа при изохорическом процессе равна C_V? [решение]

 1.Ш Два разноименных заряда q₁ = 20 мкКл и q₂ = -30 мкКл находятся в вакуме на расстоянии r = 50 см друг от друга. Найдите моуль напряженности E электростатического поля в точке, находящейся на расстоянии соответственно r₁ = 40 см и r₁ = 30 см от данных зарядов. [решение]

   2.Ш К закрепленному шарику, заряженному зарядом −q, движется электрон. На расстоянии r = r_o скорость электрона v_o. Определите, на какое минимальное расстояние r_min приблизится электрон к шарику. [решение]

   3(РГУНГ 2003). Две частицы, имеющие массы 2 г и 3 г и одинаковые заряды 6 мкКл, приближаются друг к другу. В некоторый момент они находятся на расстоянии 30 м и имеют одинаковые скорости 3 м/с. Найдите наименьшее расстояние между частицами в процессе движения. Коэффициент в законе Кулона k = 9 × 10⁹ м/Ф. [решение]

   4(РГУНГ 2007). Шарик массой 5 г с зарядом 2 мКл подвешен на нити в горизонтальном электрическом поле с напряженностью 20 В/м, направленной слева направо. Шарик с нитью отводят вправо до горизонтального положения нити и отпускают. Найдите натяжение нити (в мН) в тот момент, когда она впервые составит с вертикалью угол α (cosα = 0,8). [решение]

   5(МИФИ 1972). Заряженный шарик массой m = 1 г висит на нерастяжимой изолирующей нити. Определить работу, которую необходимо совершить, приближая к нему издалека и очень медленно другой заряженный шарик, помещая его в точку, где вначале находился шарик на нити, который отклоняется при этом, поднимаясь на высоту h = 1 см. [решение]

   6(МИФИ 1974). Два небольших шарика A и B, каждый массой m = 0,1 кг, имеют одинаковые по модулю и противоположные по знаку заряды q = 10⁻⁶ Кл. Шарик A подвешен на изолирующей пружинке с жесткостью k = 9,8 H/м над шариком B, как показано на рисунке. В начальном положении сила кулоновского взаимодействия между шариками равна 4mg. Верхний конец пружинки начали медленно поднимать. На сколько сантиметров надо переместить точку O, чтобы натяжение изолирующей и нерастяжимой нити BCобратилось в нуль? [решение]

   7(МИФИ 1982). Два одинаковых заряженных шарика, масса и заряд каждого из которых равны m = 10 г и q = 5 × 10⁻⁷ Кл, соединены двумя изолирующими нитями длины l = 10 см и 2l (рис.). Систему удерживают за середину длинной нити, а затем точку подвеса O начинают поднимать вверх с ускорением a, равным по модулю ускорению свободного падения g. Определите натяжение короткой нити, соединяющей шарики, во время их подъема. [решение]

   8(НГУ 1975). В тонкостенной непроводящей равномерно заряженной зарядом Q сфере радиуса R и массы М имеются два небольших диаметрально противоположных отверстия. В начальный момент сфера покоится. По прямой, соединяющей отверстия, из бесконечности начинает двигаться со скоростью v частица массы m с зарядом q, одноименным с Q. Найти время, в течение которого заряд q будет находиться внутри сферы. [решение]

   9(НГУ 1975). Две частицы с массами m и M и противоположными зарядами под влиянием взаимного электрического притяжения движутся по окружностям. Скорость частицы с массой m мгновенно увеличивают, не изменяя ее направлении. В какое минимальное число раз нужно увеличить скорость, чтобы частицы после этого разлетелись неограниченно далеко друг от друга? [решение]

   10(НГУ 1975). На горизонтальной поверхности расположены закрепленный заряд Q и на расстоянии r_o от него масса m с одноименным зарядом q, которая может перемещаться вдоль поверхности с коэффициентом трения μ. В начальный момент масса mпокоилась, а затем начала двигаться под действием закрепленного заряда. На каком расстоянии от заряда Q она остановится? Ускорение силы тяжести g. [решение]

   11(НГУ 1980). Посередине плоского конденсатора, расстояние между пластинами которого 2l. находится заряженная сетка (рис.). Разность потенциалов между положительно заряженной пластиной B и сеткой вдвое больше разности потенциалов между сеткой и отрицательно заряженной пластиной A. Из пластины A под углом α к ее плоскости вылетает положительно заряженная частица и достигает точки, расположенной на расстоянии 1/2 от пластины B. Определите, на каком расстоянии от точки вылета частица попадает на пластину A. Силу тяжести не учитывать. [решение]

   12(НГУ 1994). На горизонтальной плоскости с коэффициентом трения μ покоились два тела с массами M и m заряженные разноименными зарядами Q и −Q. Тело массой m начинают медленно двигать к другому телу до тех пор, пока оно не начнет скользить дальше само. В тот момент, когда тело массой М сдвигается с места, электрические заряды быстро убирают. Во сколько раз должны отличаться массы, чтобы тела коснулись друг друга при их дальнейшем движении? Размеры тел считайте малыми. [решение]

   13(НГУ 1995). Маятник, имеющий на конце нити шарик массой m и зарядом q, находится в поле тяжести и однородном электрическом поле, напряженность E которого перпендикулярна ускорению свободного паления g. Маятник отклоняют до горизонтального положения в плоскости векторов E и g и отпускают. Найдите натяжение нити, когда маятник будет проходить положение равновесия в данных полях. [решение]

   14(НГУ 1997). На невесомом стержне длины L висит маленький шарик массы m с зарядом Q. На короткое время t включается постоянное горизонтальное электрическое поле напряженностью E. Найдите максимальный угол отклонения стержня от вертикали. [решение]

   15(НГУ 1998). Связанные нитью шарики массы m и M, которые имеют одинаковые заряды q, летят по направлению нити с равными скоростями v. Нить пережигают. Какова была длина нити, если после разлета шарик массы m остановился? [решение]

   16(НГУ 1998). На горизонтальную пластинку площади S с отрицательным зарядом −Q оседают из воздуха пылинки, масса каждой из которых m, а заряд +q. Какова наибольшая масса слоя пыли, осевшей на пластину? Ускорение свободного падения g. [решение]

   17(НГУ 1999). Внутренние металлические пластины заряжены зарядами q и −q соответственно. Внешние исходно незаряженные металлические пластины соединяют через сопротивление. Какой заряд пройдет через сопротивление, и какое количество теплоты выделится в нем? Расстояние между соседними пластинами d, площадь каждой пластины S. Линейный размер пластин много больше расстояния между ними. [решение]

   18(НГУ 2000). На нижнем конце неподвижной вертикально расположенной в поле тяжести спицы закреплена бусинка с зарядомq₁. Вторая бусинка с зарядом q₂ и массой m может свободно двигаться вдоль спицы. В начальный момент времени вторая бусинка имела нулевую скорость и находилась на высоте h над первой. Найти максимальную скорость второй бусинки. Ускорение свободного падения g. [решение]

   19(НГУ 2000). Три частицы с одинаковыми зарядами находятся в вершинах равнобедренного прямоугольного треугольника. При какой массе M частицы, находящейся в вершине прямого угла, все частицы при разлете будут находиться в вершинах подобного треугольника? Массы двух остальных частиц равны m. [решение]

   20(НГУ 2000). Два тела с массами m₁ и m₂ и зарядами q и −q соединены пружиной жесткости k и находятся в состоянии покоя (пружина не растянута). Мгновенно включается электрическое поле E, направленное вдоль пружины. Найти максимальные значения скоростей первого и второго тела при последующем движении. Электрическим взаимодействием тел между собой пренебречь. [решение]

 1(НГУ). Оцените сопротивление и мощность бытовой электрической лампочки накаливания сразу после ее включения. Предполагается, что Вы хорошо представляете явление, можете сами задать недостающие и необходимые для решения задачи величины, выбрать их числовые значения и получить численный результат. [решение]

   2(МГУ). Электрическая лампа с вольфрамовой нитью рассчитана на напряжение U = 220 B и потребляет в рабочем режиме мощность P = 100 Вт. Сопротивление отключенной от сети лампы при температуре 0 °С равно R_o = 40 Ом. Найдите температуру tнити лампы в рабочем режиме, если температурный коэффициент сопротивления вольфрама α = 4,1 × 10⁻³ К⁻¹. Изменением длины нити при нагреве пренебречь. [решение]

   3(МГУ). Спираль, свернутая из стальной проволоки, подключена к источнику постоянной ЭДС с пренебрежимо малым внутренним сопротивлением. Во сколько раз α изменится время нагрева определенного количество воды от комнатной температуры до температуры кипения, если заменить эту спираль на стальную спираль той же массы, свернутую из проволоки, имеющей в β = 2 раза меньшую длину? Потерями тепла пренебречь. [решение]

   4(МГУ). Две одинаковые лампочки мощностью P = 100 Вт каждая, рассчитанные на напряжение U_o = 127 B, включены в сеть напряжением U = 220 B параллельно. При каком сопротивлении резистора R, присоединенного к лампочкам последовательно, лампочки горят в нормальном режиме? [решение]

   5(МГУ). Два одинаковых вольтметра, соединенных последовательно, при подключении к источнику тока показывают напряжениеU₁ = 4,5 B каждый. Если к тому же источнику подключить один вольтметр, он показывает напряжение U₂ = 8 B. Чему равна ЭДС источника? [решение]

   6(МГУ). Амперметр, включенный в участок цепи, изображенный на рисунке, показывает силу тока I₁ = 0,5 А. Найдите силу тока через резистор R₄. Сопротивления резисторов: R₁ = R₄ = 2 Ом; R₂ = 4 Ом, R₃ = R₅ = 1 Ом. Сопротивлением амперметра пренебречь. [решение]

   7(НГУ). Определить заряды на конденсаторах в цепи, изображенной на рисунке. Внутренним сопротивлением батареек пренебречь. До включения в цепь заряд на пластинах конденсаторов был равен нулю. [решение]

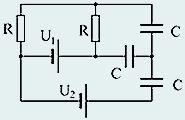
   8. На рисунке представлен замкнутый контур некоторой разветвленной электрической цепи. Определите заряды конденсаторовC₁, C₂ и C₃. Если C₁ = C₃ = С, C₂ = 2С, R₁ = R, R₂ = 2R, сила тока задана и направлена слева направо. [решение]

   9. Определите заряд q на конденсаторе C. Внутреннее сопротивление источника пренебрежимо мало. [решение]

 10. Электромотор питается от сети с напряжением U = 24 В. Чему равна мощность на валу мотора при протекании по его обмотке тока I = 8 А, если известно, что при полном затормаживании якоря по цепи идет ток I_o = 16 А? [решение]

 11. Электропоезд идет по горизонтальному пути со скоростью v₁, на его пути имеется подъем с уклоном α = 0,04. На горизонтальном участке потребляемая сила тока I₁ = 240 A, а на подъеме потребляемая сила тока I₂ = 450 A. Если коэффициент сопротивления движению равен μ = 0,02, то отношение скоростей v₁/v₂ равно … [решение]

   1. Частица массой m = 10⁻⁴ г, несущая заряд q = 10⁻⁷ Кл, движется в плоскости, перпендикулярной однородному магнитному полю с индукцией В = 1 Тл. Найти период обращения частицы Т. Силу тяжести не учитывать. [решение]

   2. Заряженная частица массой m = 6,4 × 10⁻²⁷ кг влетает со скоростью v _o = 100 км/с в область с постоянным и однородным магнитным полем, вектор индукции которого В перпендикулярен v _o. На какой угол α отклонится частица, если область, занимаемая магнитным полем, в котором движется частица, ограничена плоскостями, перпендикулярными v _o, расстояние между которыми L = 10 см? Заряд частицы q = 3,2 × 10⁻¹⁹ Кл, индукция магнитного поля В = 0,01 Тл. Силу тяжести не учитывать. [решение]

   3. Квадратная проволочная рамка может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из ее сторон. Рамка помещена в однородное магнитное поле с индукцией B, направленной вертикально. Когда по рамке течет ток I = 5 А, она отклоняется от вертикальной плоскости на угол α = 30^o. Определить индукцию магнитного поля В, если площадь сечения проволоки, из которой изготовлена рамка, S = 4 мм², а плотность материала проволоки ρ = 8,6 × 10³ кг/м³. Ускорение свободного падения принять g = 10 м/с². [решение]

   4. Два бесконечно длинных прямых проводника скрещены под прямым углом. По проводникам текут токи I₁ = 80 А и I₂ = 60 А. Расстояние между проводниками d = 10 см. Чему равна магнитная индукция в точке А, одинаково удаленной от обоих проводников? [решение]

   5. Квадратная проволочная рамка ACDE со стороной l = 0,2 м помещена в магнитное поле с индукцией В = 0,7 Тл, причем вектор Вперпендикулярен плоскости рамки (рис.).

По рамке с постоянной скоростью v = 0,6 м/с скользит перемычка MN, сделанная из той же проволоки. Найти разность потенциалов точек С и D в момент, когда перемычка находится: а) посередине рамки; б) у правого края рамки. [решение]

 6(K). Медное кольцо радиусом r = 5 см помещают в однородное магнитное поле с индукцией В = 8 мТл перпендикулярно линиям индукции. Какой заряд пройдет по кольцу, если его повернуть на 180° вокруг оси, совпадающей с его диаметром? Сопротивление единицы длины кольца ρ_l = 2 мОм/м. [решение]

 7(К). Сторона прямоугольного каркаса, имеющая длину l = 10 см, скользит со скоростью v = 1 м/с по двум другим сторонам, оставаясь с ними в электрическом контакте. Плоскость прямоугольника перпендикулярна линиям индукции однородного магнитного поля В = 0,01 Тл. Найдите силу тока в прямоугольнике через t = 0,9 с после начала движения. Сопротивление единицы длины провода ρ_l = 1 Ом/м. В начальный момент площадь прямоугольника равна нулю. [решение]

 8(K). Самолет летит горизонтально со скоростью v = 900 км/ч. Найдите разность потенциалов, возникающую между концами его крыльев, если вертикальная составляющая индукции магнитного поля Земли В_верт = 50 мкТл, а размах крыльев l = 12 м. [решение]

 9(K). С какой угловой скоростью надо вращать прямой проводник вокруг оси, проходящей через один его конец, в плоскости, перпендикулярной линиям однородного магнитного поля с индукцией В = 0,2 Тл, чтобы в проводнике возникла ЭДС индукции E_инд= 0,3 В? Длина проводника l = 20 см. [решение]

 10(K). Из проволоки, сопротивление единицы длины которой ρ_l = 0,1 Ом/м, сделали квадрат и поместили его в однородное магнитное поле с индукцией В = 4 мТл перпендикулярно линиям поля. По двум противоположным сторонам квадрата скользит со скоростью v = 0,3 м/с перемычка из такой же проволоки, оставаясь параллельной двум другим сторонам. Чему равен ток через перемычку в тот момент, когда она делит квадрат пополам. [решение]

 11(K). Длинную проволоку согнули под углом а таким, что sinα = 0,6, и поместили в однородное магнитное поле с индукцией В = 0,1 Тл перпендикулярно линиям поля. Вдоль сторон угла равномерно перемещают перемычку из такой же проволоки так, что она все время образует прямой угол с одной из его сторон. В начальный момент перемычка находится на расстоянии х₁ = 0,2 м, а через время t = 1 с − на расстоянии х₂ = 0,6 м от вершины угла. Какое количество теплоты выделилось в системе за это время? Сопротивление единицы длины проволоки ρ_l = 0,01 Ом/м. [решение]

 12(K). По П-образной рамке, помещенной в однородное магнитное поле, перпендикулярное плоскости рамки, движется без трения с постоянной скоростью v = 2 м/с перемычка, сопротивление которой R = 2 Ом. К перемычке приложена сила F = 4 H. Найдите силу тока в перемычке. Сопротивлением рамки пренебречь. Силу тяжести не учитывать. [решение]

 13(K). По П-образной рамке, наклоненной под углом α = 30° к горизонту и помещенной в однородное вертикальное магнитное поле, начинает соскальзывать без трения перемычка массой m = 30 г. Длина перемычки 1 = 10 см, ее сопротивление R = 1 мОм, индукция магнитного поля В = 0,1 Тл. Найдите установившуюся скорость движения перемычки. Сопротивлением рамки пренебречь. [решение]

 14(K). Замкнутый контур образован двумя вертикальными рейками, между нижними концами которых включен источник тока с ЭДС E = 60 мВ и внутренним сопротивлением r = 1 мОм, а верхние концы замкнуты перемычкой длиной l = 10 см и массой m = 10 г. Контур находится в перпендикулярном его плоскости однородном магнитном поле с индукцией B = 0,1 Тл. Когда перемычку освобождают, она начинает опускаться. Пренебрегая сопротивлением реек и перемычки, а также трением, найдите установившуюся скорость перемычки. [решение]

 15(K). По вертикальной П-образной рамке, помещенной в однородное магнитное поле, перпендикулярное плоскости рамки, может без трения скользить перемычка. В короткую сторону рамки включена катушка индуктивностью L = 0,4 мГн. Масса перемычки m = 10 г, ее длина l = 10 см, индукция поля В = 0,1 Тл. Перемычку сначала удерживают на месте, затем отпускают. Пренебрегая сопротивлениями всех элементов цепи, найдите максимальную скорость и максимальное смещение перемычки. [решение]

  1. В колебательном контуре с индуктивностью L и емкостью С конденсатор заряжен до максимального напряжения U_M. Каким будет ток I в контуре в тот момент, когда напряжение на конденсаторе уменьшится в два раза? Колебания считать незатухающими. [решение]

   2. В колебательном контуре конденсатору с емкостью С = 10 мкФ сообщили заряд q = 1 мКл, после чего возникли затухающие электромагнитные колебания. Сколько тепла Q выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше начального максимального напряжения в n = 4 раза? [решение]

   3. Катушка индуктивностью L = 2 мГн с сопротивлением обмотки R = 10 Ом и конденсатор емкостью С = 10⁻⁵ Ф подключены параллельно к источнику с ЭДС E = 100 В и внутренним сопротивлением r = 10 Ом. Какое количество тепла Q выделится в контуре после отключения источника? [решение]

   4. Конденсатор емкостью С = 0,1 мкФ, заряженный до напряжения U = 100 В, подсоединяют к катушке индуктивностью L = 1 мГн. Чему равна величина тока I через катушку спустя время t_o = 0,785 × 10⁻⁵ с после подключения конденсатора? Сопротивлением катушки и соединительных проводов пренебречь. [решение]

   5. Колебательный контур состоит из катушки индуктивности и четырех конденсаторов, соединенных как показано на рисунке. Во сколько раз а изменится период собственных колебаний в контуре, если замкнуть ключ, соединяющий точки А и В? С₁ = 10⁻⁸ Ф, С₂= 4 × 10⁻⁸ Ф. [решение]

   6. В цепи, показанной на рисунке, конденсатор емкостью С₁ = 10⁻⁵ Ф вначале заряжен до напряжения U₁ = 200 В, а конденсатор емкостью С₂ = 10⁻⁶ Ф разряжен. До какого максимального напряжения U_2max может зарядиться конденсатор С₂ в процессе колебаний, возникающих в цепи после замыкания ключа? Потерями в соединительных проводах и в катушке индуктивности пренебречь. [решение]

   7. Катушка индуктивностью L = 3 мГн подключена к двум последовательно соединенным конденсаторам (см. рисунок), один из которых, емкостью С₁ = 10⁻⁷ Ф, заряжен вначале до напряжения U₁ = 150 В, а второй, емкостью C₂ = 3 × 10⁻⁷ Ф, разряжен. Чему будет равна максимальная сила тока I_max в этой цепи после замыкания ключа? [решение]

Колебания и волны. Задачи для абитуриентов.

 1. Определите период колебаний малых колебаний математического маятника длиной 15 см, подвешенного к потолку вагона, движущегося с ускорением 5 м/с². [решение]

 2. Найдите период колебаний T идеальной жидкости плотностью ρ, налитой в U-образную трубку площадью поперечного сеченияS до высоты h. [решение]

 3. Определите период колебаний T шарика, скользящего без трения вниз и вверх по двум гладким наклонным плоскостям, расположенным под углом α и β. [решение]

 4. К свободному концу легкой вертикальной пружины, прикрепленной к потолку, осторожно подвешивают груз и отпускают без начальной скорости. Амплитуда возникших колебаний A = 40 мм. Определите период T колебаний и максимальную скорость движения груза. [решение]

 5. На какую часть необходимо уменьшить длину математического маятника, чтобы период его колебаний T на высоте 10 км над поверхностью Земли был равен его периоду колебаний на поверхности на поверхности? [решение]

 6. Определите период колебаний плавающего в воде соснового кубика с ребром 3 см. [решение]

 7. В открытые сообщающиеся сосуды с площадью поперечного сечения S и 2S налита ртуть массой m. Столбик ртути в одном из сосудов вывели из положения равновесия, вследствие чего она начала колебаться. Определить период колебаний ртути. [решение]

 8. В неподвижном лифте висит маятник, период колебаний которого T = 1 c. С каким ускорением движется лифт, если период колебаний этого маятника стал T₁ = 1,1 c? В каком направлении движется лифт? [решение]

 9. Как изменится период колебания математического маятника, если его точку подвеса двигать:

1. вертикально вверх с ускорением а,

2. вертикально вниз с ускорением a < g,

3. горизонтально с ускорением a. [решение]

 10. В некоторой среде распространяется волна. За время, в течение которого частица среды совершает n = 140 колебаний, волна распространяется на расстояние l = 110 м. Найти длину волны λ. [решение]

Оптика волновая. Задачи для абитуриентов.

   1. Какую наименьшую толщину должна иметь мыльная пленка, чтобы отраженные лучи имели красную окраску (λ = 0,63 мкм)? Белый луч падает на пленку под углом α = 30^o (n = 1,33). [решение]

   2. На дифракционную решетку (Д) нормально падает монохроматический свет с длиной волны 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние 0,5 м, наблюдается дифракционная картина. Расстояние между дифракционными максимумами первого порядка равно 10 см. Определить постоянную дифракционной решетки и общее число главных максимумов, получаемых с помощью этой решетки. [решение]

   3. От источника излучения с длиной волны λ свет падает на тонкую прозрачную пленку толщиной d с показателем преломления n(относительно воздуха). Определите результат интерференции для светового пучка, отраженного под небольшим углом α? Почему интерференционная картина не возникает на прозрачных пластинах значительной толщины (оконное стекло, например)? [решение]

 4. Два когерентных пучка света падают на экран: один по нормали, а другой − под углом α = 0,01 рад. Найти период dинтерференционной картины, т.е. расстояние между соседними светлыми полосами на экране, если длина световой волны в обоих пучках равна λ = 0,5 мкм. [решение]

 5. На стеклянную пластинку нанесен тонкий слой прозрачного покрытия, показатель преломления которого n = 1,41 меньше показателя преломления стекла. На пластинку под углом α = 30° падает пучок белого света. Какова минимальная толщина покрытия dmin, если в отраженном свете оно кажется зеленым? Длина волны зеленого света λ = 0,53 мкм. [решение]

1. Где видит наблюдатель рыбку, находящуюся в диаметрально противоположной от него точке шарообразного аквариума? Радиус аквариума R, показатель преломления воды n = 4/3. [решение]

 2. Стеклянная прямоугольная призма поставлена на монету (рис.). Коэффициент преломления стекла равен 1,5. Доказать, что монету нельзя увидеть через боковую грань призмы. [решение]

 3. Стержень опущен концом в прозрачную жидкость, показатель преломления которой равен n, и образует с поверхностью жидкости угол α. Наблюдателю, который смотрит сверху, конец стержня, погруженный в жидкость, кажется смещенным на угол β(рис.). При каком угле наклона стержня α угол смещения β будет максимальным? [решение]

 4. Плоскопараллельная пластинка находится в воздухе. Ход светового луча в пластинке показан на рисунке.

Показатель преломления материала пластинки равен:    1) 1,5; 2) 1,6; 3) 1,7; 4) 1,8; 5) 1,9. [решение]

 5. На стеклянную призму с преломляющим углом θ = 50° падает под углом ε = 30° луч света. Определить угол отклонения σ луча призмой, если показатель преломления n стекла равен 1,56. [решение]

 6. Оптическая система представляет собой тонкую плосковыпуклую стеклянную линзу, выпуклая поверхность которой посеребрена. Определить главное фокусное расстояние f такой системы, если радиус кривизны R сферической поверхности линзы равен 60 см. [решение]

 7. Точечный источник света расположен на дне водоема глубиной h = 0,6 м. В некоторой точке поверхности воды вышедший в воздух преломленный луч оказался перпендикулярным лучу, отраженному от поверхности воды обратно в воду. На каком расстоянииL от источника на дне водоема достигнет дна отраженный луч? Показатель преломления воды n = 4/3. [решение]

 8. Луч света падает на плоскопараллельную стеклянную пластину толщины d = 2 см под углом α = 30°. Какое расстояние абудет между лучами: прошедшим пластину без отражения (А) и претерпевшим двукратное отражение от ее граней (Б)? Показатель преломления стекла n = 1,5. [решение]

 9. На поверхности воды плавает непрозрачный шар радиусом R = 1 м, наполовину погруженный в воду. На какой максимальной глубине H_max нужно поместить под центром шара точечный источник света, чтобы ни один световой луч не прошел в воздух? Показатель преломления воды n = 1,33. [решение]

 10. В стекле с показателем преломления n₁ = 1,5 имеется сферическая полость радиуса R = 4,5 см, заполненная водой. Показатель преломления воды n₂ = 4/3. На полость падает широкий пучок параллельных световых лучей. Определить радиус rпучка световых лучей, которые проникают в полость. [решение]

 11. Два параллельных луча, расстояние между которыми равно радиусу R круглого прямого прозрачного цилиндра, падают на боковую поверхность этого цилиндра. Лучи параллельны основанию цилиндра. Найти величину показателя преломления n материала цилиндра, при которой лучи пересекаются на его поверхности. [решение]

 12. Луч света падает на стеклянный полушар радиуса R на расстоянии а от его оси симметрии параллельно ей. На какой угол α отклонится вышедший после преломления в полушаре луч, если а = 0,5R, n = 1,414? [решение]

 13. Световой луч падает на поверхность стеклянного шара. Угол падения α = 45°, показатель преломления стекла n = 1,41. Найти угол γ между падающим лучом и лучом, вышедшим из шара. [решение]

 14. На стеклянный шар радиусом R с показателем преломления n падает узкий пучок света, образуя угол α с осью, проведенной через точку падения и центр шара. На каком расстоянии d от этой оси пучок выйдет из шара? [решение]

 15. На поверхность стеклянного шара с показателем преломления n < 2 падает узкий пучок света, образуя малый угол α с осью шара, проведенной через точку падения и центр шара. Под каким углом γ к этой оси пучок выйдет из шара? При расчетах положитьsina ≈ а. [решение]

 16. Снаружи от прозрачного шара вплотную к его поверхности помещен точечный источник света. При каких значениях nпоказателя преломления материала шара все выходящие из него лучи (за исключением луча, прошедшего через центр шара) будут наклонены по направлению к оси, проведенной через источник и центр шара? [решение]

 17. Луч света, лежащий в плоскости рисунка, падает на боковую грань АВ призмы, имеющей при вершине угол 90°. В каких пределах лежат возможные значения угла падения а, если известно, что луч выходит из боковой грани АС? Показатель преломления призмы n = 1,25. [решение]

 18. Снаружи круглого прозрачного стержня вблизи от центра его торца помещен точечный источник света. При каких значениях показателя преломления материала стержня n свет не будет выходить через его боковую поверхность? [решение]

 19. Снаружи круглого прозрачного стержня вблизи от центра его торца помещен точечный источник света. Найти ширину l области на боковой поверхности стержня, через которую будут выходить наружу световые лучи. Радиус стержня R, показатель преломления n. [решение]

 20. Торец круглого прозрачного стержня с показателем преломления n освещается рассеянным светом. Под каким максимальным углом γ к оси стержня будут выходить световые лучи через его боковую поверхность? [решение]

1. Протон движется со скоростью 0,7 скорости света. Найти импульс и кинетическую энергию протона. [решение]

   2. Космическая ракета движется с большой относительной скоростью. Релятивистское сокращение ее длины составило 36 %. Определить скорость движения ракеты. [решение]

   3. Прямоугольный брусок со сторонами 3,3 и 6,9 см движется параллельно большому ребру. При какой скорости движения прямоугольный брусок превратится в куб? Как скажется движение на объеме тела? [решение]

   4. С момента образования до распада π-мезон пролетел расстояние 1,35 км. Время жизни π-мезона в неподвижной системе координат равно 5 мкс. Определить время жизни π-мезона по часам в системе координат, движущейся вместе с ним. [решение]

   5. При какой скорости движения кинетическая энергия электрона равна 5 МэВ? [решение]

   6. Определить импульс электрона, обладающего кинетической энергией 5 МэВ. [решение]

   7. Протон движется со скоростью, равной 0,8 скорости света. Навстречу ему движется электрон со скоростью 0,9 скорости света. Каковы их скорости относительно друг друга? Определить полную и кинетическую энергию электрона. [решение]

  1. Катод фотоэлемента облучается светом с длиной волны λ = 3,5 × 10⁻⁷ м. Какая энергия передана фотоэлектронам, если в цепи фотоэлемента протек заряд Q = 2 × 10⁻¹² Кл? Постоянная Планка h = 6,62 × 10⁻³⁴ Дж•с, величина заряда электрона |е| = 1,6 × 10⁻¹⁹ Кл, скорость света с = 3 × 10⁸ м/с. [решение]

   2. Какой максимальный заряд Q может быть накоплен на конденсаторе емкостью С_o = 2 × 10⁻¹¹ Ф, одна из обкладок которого облучается светом с длиной волны λ = 5 × 10⁻⁷ м? Работа выхода электрона составляет А = 3 × 10⁻¹⁹ Дж, постоянная Планка h = 6,62 × 10⁻³⁴ Дж•с, величина заряда электрона |е| = 1,6 × 10⁻¹⁹ Кл, скорость света с = 3 × 10⁸ м/с. [решение]

   3. На металлическую пластинку сквозь сетку, параллельную пластинке, падает свет с длиной волны λ = 0,4 мкм. Фототок прекращается при задерживающей разности потенциалов между пластинкой и сеткой U = 0,95 В. Определить красную границу фотоэффекта (максимальную длину волны λ_max). Постоянная Планка h = 6,62 × 10⁻³⁴ Дж•с, величина заряда электрона |е| = 1,6 × 10⁻¹⁹ Кл, скорость света с = 3 × 10⁸ м/с. [решение]

   4. Лазер излучает световые импульсы с энергией W = 0,1 Дж. Частота повторения импульсов ν = 10 Гц. Коэффициент полезного действия лазера, определяемый как отношение излучаемой энергии к потребляемой, составляет η = 0,01. Какой объем воды Vнужно пропустить за время τ = 1 час через охлаждающую систему лазера, чтобы вода нагрелась не более, чем на Δt = 10 ^oС? Удельная теплоемкость воды с = 4,2 Дж/(г•К), плотность воды ρ = 1 г/см³. [решение]

   5. Атом водорода испустил фотон с длиной волны 4,86 × 10⁷ м. На сколько изменилась энергия электрона в атоме? [решение]

   1. Вычислить дефект массы, энергию связи и удельную энергию связи ядра ¹⁶О. Масса атома водорода m(_H¹) = 1,00783 а.е.м.; масса нейтрона m_n = 1,00867 а.е.м.; масса атома кислорода m(_O¹⁶) = 15,99492 а.е.м.; Z = 8; А = 16. [решение]

   2. Ядро, состоящее из 92 протонов и 143 нейтронов, выбросило α-частицу. Какое ядро образовалось при α-распаде? Определить дефект массы и энергию связи образовавшегося ядра. [решение]

   3. В какой элемент превращается ₉₂³²⁸U после трех α-распадов и двух β-распадов? [решение]

   4. Период полураспада ₂₇⁶⁰Co равен примерно 5,3 года. Определить постоянную распада и среднюю продолжительность жизни атомов этого изотопа. [решение]

   5. Сколько ядер, содержащихся в 1 г трития ₁³H, распадается за среднее время жизни этого изотопа? [решение]

 Задача 1. За время t = 2 ч автомашина проехала расстояние S = 160 км. Двигатель развил среднюю мощность N = 70 кВт при КПД 25 %. Сколько горючего сэкономил водитель, если норма расхода m_o = 36 кг на пути S_o = 100 км? Удельная теплота сгорания топлива q = 4,2 × 10⁷ Дж/кг. [решение]

   Задача 2. Давление воздуха внутри плотно закупоренной бутылки при температуре 7 °С равно 150 кПа. До какой температуры (по шкале Цельсия) надо нагреть бутылку, чтобы из нее вылетела пробка, если известно, что для вынимания пробки до нагревания бутылки требовалась минимальная сила 90 Н? Площадь поперечного сечения пробки 8 см². [решение]

   Задача 3. Железная деталь массой m₁ = 500 г, нагретая до температуры t₁ = 800 °С, опущена в воду. При этом образовалось некоторое количество пара (его температуру считайте равной t_к = 100 °С), а температура воды повысилась на величину Δt = 1 °С. Определите массу образовавшегося пара, если объем первоначальной воды V₂ = 5,0 л, ее температура t₂ = 19 °С, плотность ρ₂ = 1,0 г/см³, удельная теплоемкость c₂ = 4,2 кДж/(кг•град), удельная теплота парообразования L₂ = 2,3 МДж/кг, удельная теплоемкость железа c₁ = 460 Дж/(кг•град). [решение]

   Задача 4. Какую минимальную горизонтальную скорость нужно сообщить шарику, подвешенному на вертикальном нерастяжимом и невесомом подвесе, чтобы шарик описал полную окружность в вертикальной плоскости. [решение]

   Задача 5. Из куска провода сделали равносторонний треугольник. Сопротивления измеренные между любыми двумя вершинами треугольника, равны R_o = 32 Ом. Определите сопротивление куска провода R. Чему равны сопротивления, измеренные между двумя вершинами квадрата, сделанного из этого куска провода? [решение]

   Задача 1. Радиус некоторой планеты в √3 раз меньше радиуса Земли, а ускорение силы тяжести на поверхности планеты в 3 раза меньше, чем на поверхности Земли. Во сколько раз масса планеты меньше массы Земли? [решение]

   Задача 2. В сосуде с вертикальными стенками находится вода. В нее опустили камень. На сколько процентов при этом изменилось гидростатическое давление воды на дно сосуда, если известно, что объем камня меньше объема воды в n = 14 раз? Считайте, что вода из сосуда не выливалась. [решение]

   Задача 3. В калориметре находится вода и плавающий в ней лед. В воду опустили нагреватель и начали через каждую минуту измерять ее температуру. В течение первой и второй минут температура воды не изменялась, к концу третьей минуты повысилась на величину Δt₁ = 2,0 °С и к концу четвертой − еще на величину Δt₂ = 5,0 °С. Определите массу воды и массу льда, первоначально содержащихся в калориметре, если мощность нагревателя P = 60 Вт, его КПД η = 81 %. Удельная теплоемкость воды с = 4,2 кДж/(кг•град), удельная теплота плавления льда λ = 0,33 МДж/кг. Теплоемкость калориметра и потери теплоты не учитывайте. [решение]

   Задача 4. Два маленьких металлических шарика одинакового радиуса r зарядили одноименными зарядами q₁ и q₂, и расположили их на расстоянии R друг от друга. Затем шарики на небольшое время соединили тонкой проволочкой.

1. Как при этом изменилась (увеличилась или уменьшилась) энергия взаимодействия

2. При каком условии это изменение максимально?

3. Чему оно равно?

4. Какое количество теплоты выделилось в проволочке за время соединения шариков? Считайте R >> r. [решение]

   Задача 5. Мост в форме выпуклой параболы перекинут через реку шириной l = 100 м. Самая верхняя точка моста находится над уровнем берегов на высоте h = 5 м. Автомашина массой m = 1000 кг движется по мосту с постоянной скоростью v = 20 м/с. Определите силу давления автомашины на мост в самой верхней его точке. [решение]

1.В стакане, наполненном до краёв водой, плавает кусок льда. Перельётся ли вода через край, когда лёд растает? Что произойдёт, если в стакане находится не вода, а 1) жидкость более плотная, 2) жидкость менее плотная?

2. В массивную трубку вставлена пружина, которая в свободном состоянии занимает всю длину трубки. На пружину положен шарик, который сжимает её примерно вдвое. Затем трубка начинает в наклонном положении свободно падать. Что произойдёт с шариком?

3. Комната освещена с помощью 40 электрических лампочек от карманного фонаря, соединённых последовательно и питаемых от городского тока. После того как одна лампочка перегорела, оставшиеся 39 лампочек снова соединили последовательно и включили в сеть городского тока. Когда в комнате было светлее: когда горело 40 лампочек или когда горело 39 лампочек? Почему?

4. Пассажир бежит вниз по эскалатору, идущему вниз, и считает ступеньки. Пробежав весь эскалатор, он насчитал100 ступенек. Проделав то же самое на эскалаторе, идущем вверх, он насчитал300 ступенек. Сколько ступенек он насчитал бы на неподвижном эскалаторе?

5. Сухие дрова плотностью ρ₁ = 600 кг/м³, привезенные со склада, свалили под открытым небом и ночью ничем не укрыли. Дрова промокли, и их плотность стала равной ρ₂ = 700 кг/м³. Для того чтобы в холодную, но не морозную погоду (при температуре t = 0 °C) протопить дом до комнатной температуры, нужно сжечь в печи М₁ = 20 кг сухих дров. Оцените, сколько нужно сжечь мокрых дров, чтобы протопить дом до той же комнатной температуры? Удельная теплота парообразования воды L = 2,3·10⁶ Дж/кг, удельная теплоемкость воды с = 4200 Дж/(кг·°C), удельная теплота сгорания сухих дров r =1,0 10⁷ Дж/кг.

10. класс (на конверте указывается Ф-10)

1. На веревке в петле в горизонтальном положении висит полено, один конец которого толще другого. Полено разрезают в том месте, где была петля. Одинаковы ли массы получившихся частей?

2. Вниз по реке плывет плот. Дви­жется ли он относительно воды? Если да, то в какую сторону? Чем объясня­ется это движение?

3. В ванну за одну секунду вливается кг воды, нагретой до температуры. Известно, что теплоотдача от ванны составляетгдеДж/(c,- температура окружающего воздуха. Определите установившуюся температуру воды в ванне, если уровень воды поддерживается постоянным за счет вытекания ее из ванны. Считайте, что втекающая вода успевает полностью перемешаться с водой, которая была в ванне. Удельная теплоемкость воды Дж/(кг.

4. По гладкому горизонтальному столу скользит однородная линейка длиной 50 см. В некоторый начальный момент времени скорости концов линейки направлены перпендикулярно к ней в разные стороны и равны см/с исм/с. Какая скоростьбудет у центральной точки линейки через времяпосле начального момента? За какое времяот начального момента линейка повернется на угол 90⁰ от исходного положения?

5. Тело массой М = 10 кг подвешено в лифте при помощи трех одинаковых легких веревок, натянутых вертикально. Одна из них привязана к потолку лифта, две другие – к полу. Веревки натянуты так, что в покое натяжение каждой из нижних веревок составляет F₀ = 5 Н. Найдите силу натяжения верхней веревки при ускорении лифта, равном a₁ = 1 м/с² и направленном вверх. То же – при величине ускорения лифта a₂ = 2 м/c². Ускорение свободного падения принять равным g = 9,8 м/c².