FTF 2 semestr.MARTINOV / 3

Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом  (набла). В прямоугольных декартовых координатах оператор набла определяется следующим образом:

,

где  — единичные векторы по осям x, y, z.

Через оператор набла выражаются основные операции : grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа.

Под n-мерным оператором набла подразумевается вектор с компонентами  в n-мерном пространстве.

Свойства оператора набла

1. Если умножить вектор 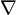 на скаляр 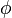, то получится вектор

,

который представляет собой градиент функции .

2. Если вектор 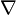 скалярно умножить на вектор 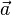, получится скаляр

,

то есть дивергенция вектора .

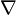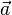3. Если  умножить на  векторно, то получится ротор вектора :