FTF 1 semestr.MAVRODI / 12

Подпоследовательности, частичные пределы.

- Пусть задана последовательность . Рассмотрим строго возрастающую последовательность

, т.е. такую, что . Тогда последовательность, где , называется подпоследовательностью последовательности и обозначается .

- Пусть - подпоследовательность последовательности 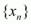, и пусть существует конечный или бесконечный . Тогда а называют частичным пределом последовательности .

Теорема Больцано-Вейерштрасса.

Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Док-во:

Пусть - ограниченная последовательность. Тогда . Разобьем отрезок пополам точкой d. Тогда по крайней мере один из отрезков [a,d], [d,b] содержит

бесконечно большое число членов последовательности . Если оба отрезка обладают этим свойством, возьмем, например, правый отрезок (и будем так поступать в дальнейшем). Выбранный

отрезок, содержащий бесконечное число членов данной последовательности, обозначим ,

его длина равна . Разделив отрезок пополам, выберем указанным выше способом из двух получившихся отрезков отрезок , содержащий бесконечное число последовательности . Продолжая эти рассуждения, получим последовательность отрезков таких, что:

1) ;

2) при .

Значит, - стягивающаяся последовательность отрезков. По т.Кантора существует единственная точка c, принадлежащая всем отрезкам, т.е. (1). Покажем, что найдётся подпоследовательность последовательности такая, что 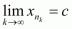(2). Т.к.

отрезок содержит бесконечное число членов последовательности , то .

Отрезок также содержит бесконечное число членов последовательности ,