ТЭС-уч.-к Дормидонт

ХФ h(X ) отображает сообщение X произвольной длины l в последова-

тельность символов (хэш-код H ) фиксированной длины m ; для снижения ско-

рости выбирают ml <<1.

Если различные сообщения X отображаются в один и тот же хэш-код, то такая ХФ допускает коллизии (склеивания) сообщений.

Основными свойствами ХФ являются чувствительность к изменениям текста сообщения, отсутствие эффективных алгоритмов поиска коллизий, однонаправленность и простота вычисления

Одной из важнейших характеристик ХФ является индекс хэширования (склеивания) I (h, S ) функции h , где S – словарь множества сообщений {X }. Ес-

ли I (h, S )= 0 , то коллизий не происходит; каждое сообщение хэшируется в свой,

отличный от других, хэш-код. ХФ, обеспечивающие I (h, S )= 0 , называются со-

вершенными ХФ.

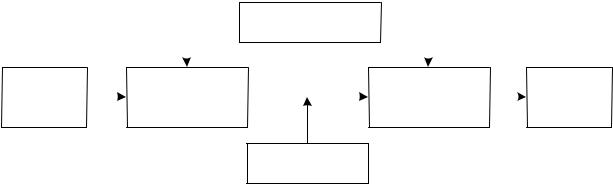
Если в процессе хэширования сообщений используется секретный ключ K , то такая функция H = h(X , K ) называется криптографической ХФ с секрет-

ным ключом (рис. 10.5,а). Криптографические ХФ, не использующие секретно-

быть разделены на однонаправленные ХФ и устойчивые к коллизиям ХФ.

Большинство известных бесключевых ХФ основано на разбиении произвольно длинных сообщений на блоки фиксированной длины и их последовательной обработке криптографической ХФ. Этот метод называется итеративным хэшированием. Хэшируемое сообщение X делится на i блоков от X1 до

Xi длиной по b бит. Если длина сообщения не кратна длине блока, то сообще-

421

ние должно дополняться до длины, кратной длине блока. Для инициализации процесса итеративного хэширования необходимо задать стартовый вектор хэширования H0 длиной n бит. Хэширование сообщения осуществляется на ос-

Криптографические ХФ в настоящее время широко используются для обеспечения безопасности информации (установление подлинности сообщений) и аутентификации пользователей криптографических систем и сетей.

В криптографических системах защиты информации ХФ используют для формирования дешифрующих последовательностей в шифрообразующих устройствах, для обеспечения секретности непрерывных и дискретных сообщений, а также для формирования случайных чисел в криптографических системах и во многих других приложениях.

422

10.3. Модели криптографических систем 10.3.1. Системы шифрования

Среди криптографических систем, обеспечивающих сохранение информации в тайне, наибольшее распространение получили системы шифрования информации. Рассмотрим обобщенную модель системы шифрования представленную на рис. 10.6.

нарушитель

Рис. 10.6. Обобщенная модель системы шифрования информация

Источник сообщений генерирует сообщения x , которые необходимо сохранить в тайне от нарушителя при передаче по незащищенному каналу. В системе имеется защищенный от нарушителя источник ключевой информации, который вырабатывает некоторый ключ e , предназначенный для шифрования сообщений отправителем сообщений и ключ d , предназначенный для дешифрования криптограмм получателем. Ключи шифрования и дешифрования связаны друг с другом и позволяют восстановить сообщение из криптограммы. Сформированная ключевая информация передается по защищенному каналу ее доставки. Под защищенным будем понимать канал передачи информации, в котором нарушитель не способен на успешные атаки. Отправитель сообщений шифрует сообщение x по ключу e , используя шифрующее преобразование c = Ee (x).

Образованная криптограмма c передается по незащищенному каналу передачи информации получателю. На приеме получатель способен из криптограммы однозначно восстановить сообщение x по ключу d , используя дешифрующее преобразование

Для однозначного восстановления сообщения из криптограммы требует-

423

ся, чтобы дешифрующее преобразование D являлось обратным к шифрующему преобразованию E при использовании ключей d и e соответственно

Системы шифрования информации разделяются на два больших класса: симметричные и несимметричные. Система шифрования информации называется симметричной, если для любой допустимой пары ключей (e, d ) вычисли-

тельно просто определить один ключ, зная другой, т.е. из e можно вычислить d и, зная d , «легко» определить e . В таких системах оба ключа должны быть секретными. Во многих симметричных системах ключ шифрования совпадает с ключом дешифрования: e = d = K . Поэтому симметричные криптосистемы иногда называют одноключевыми системами или системами с секретным ключом.

Система шифрования информации называется несимметричной, если для любой допустимой пары ключей (e, d ) вычислительно невозможно определить ключ дешифрования d , зная ключ шифрования e . В несимметричной системе шифрования ключ шифрования e может быть несекретным (открытым), известным для всех, включая нарушителя. Поэтому такие криптосистемы иногда называют системами с открытым ключом или двухключевыми системами. В таких системах должна обеспечиваться секретность ключа дешифрования d .

Несимметричные системы шифрования удобны для практического использования тем, что при доставке ключей отправителям сообщений не надо обеспечивать секретность ключевой информации шифрования сообщений.

Известно [36], что максимальная степень защищенности информации от чтения достигается, если произвольные передаваемые сообщения x и наблюдаемые нарушителем соответствующие им криптограммы c статистически независимы:

p xi cj = p(xi ).

Для приближения характеристик реальных шифраторов к характеристикам идеального используют сжатие сообщений до шифрования и рандомизацию шифруемых сообщений. Идея рандомизации заключается в уменьшении избыточности шифруемых сообщений за счет специального кодирования, обес-

424

печивающего равную вероятность появления символов, но длина сообщений при этом увеличивается.

Основной характеристикой шифра является криптостойкость, которая обычно определяется интервалом времени, необходимым для раскрытия шифра. К шифрам, используемым для криптографической защиты информации, предъявляется ряд требований:

достаточная криптостойкость (надежность закрытия данных); простота процедур шифрования и расшифрования; незначительная избыточность информации за счет шифрования; нечувствительность к небольшим ошибкам шифрования и др.

В той или иной мере этим требованиям отвечают шифры перестановок, шифры замены, шифры гаммирования и шифры, основанные на аналитических преобразованиях шифруемых данных [1, 19, 31, 36].

Шифрование перестановкой заключается в том, что символы исходного текста переставляются по определенному правилу в пределах некоторого блока этого текста. При достаточной длине блока, в пределах которого осуществляется перестановка, и сложном, неповторяющемся порядке перестановки можно достигнуть приемлемой для простых практических приложений стойкости шифра.

Шифрование заменой (подстановкой) заключается в том, что символы исходного текста заменяются символами того же или другого алфавита в соответствии с заранее обусловленной схемой замены. Возможны моно- и многоалфавитные подстановки. В случае моноалфавитных подстановок каждый символ исходного текста преобразуется в символ шифрованного текста по одному и тому же закону. При многоалфавитной подстановке преобразование меняется от символа к символу. Для обеспечения высокой криптостойкости требуется использование сложных ключей.

Шифрование гаммированием заключается в том, что символы исходного текста складываются с символами некоторой псевдослучайной последовательности, именуемой гаммой шифра. Примером может служить, поразрядное сло-

425

жение сообщения x и гаммы z при формировании криптограммы c = x z . На приеме необходимо генерировать такую же псевдослучайную последовательность ( z ) тогда дешифрование будет осуществляться на основе следующего

преобразования: ~ = = = . Стойкость шифрования определяется в

x c z x z z x

основном длиной (периодом) неповторяющейся части гаммы шифра. Поскольку с помощью ЭВМ можно генерировать гамму шифра очень большой длины, то данный способ является одним из основных для шифрования информации в автоматизированных системах.

10.3.2. Традиционные симметричные криптосистемы

Симметричные системы шифрования информации подразделяются на блочные и поточные системы.

В блочной системе шифрования информации сообщение разбивается на информационные блоки фиксированной длины n бит и весь блок шифруется одновременно. Такие системы получили название блочных шифров; они представляют собой семейство обратимых преобразований блоков исходного текста. Фактически блочный шифр это система подстановки блоков. В настоящее время блочные шифры наиболее распространены на практике. Российский и американский стандарты шифрования относятся именно к этому классу.

К элементарным блочным шифрам относятся шифры подстановки и перестановки. В шифре подстановки каждый символ сообщения заменяется символом, определяемым функцией подстановки Ee . Вид функции подстановки за-

дается ключом e . Каждый символ сообщения является информационным бло-

отображается с помощью функции подстановки Ee в соответствующий символ криптограммы того же алфавита, записанный под ним в нижней строке.

426

Если функция подстановки Ee фиксированная (ключ e является констан-

той), то такой шифр называется простой заменой, или одноалфавитной подстановкой. Такой шифр в силу его простоты широко использовался в дипломатической и военной связи несколько веков тому назад.

Например, пусть в качестве алфавита сообщений и криптограмм использован алфавит русского языка. Зададим фиксированную функцию подстановки следующим образом:

При шифровании очередной символ сообщения отыскивается в верхней строке и заменяется на соответствующий символ криптограммы, записанный снизу.

Для обеспечения однозначности операция дешифрования должна описываться подстановкой, обратной к подстановке операции шифрования.

В шифре перестановки сообщение делится на блоки фиксированной длины n и каждый символ переставляется в пределах блока в соответствии с функ-

отображает в соответствующий символ блока криптограммы, записанный под ним в нижней строке

Пусть, например, требуется зашифровать сообщение: «ПЕРЕСТАНОВКА» шифром перестановки при n = 6 . Зададим фиксированную функцию перестановки Ee вида:

«АНОВКА» длиною по 6 символов. С помощью функции перестановки полу-

427

чим блоки криптограммы «СРТПЕЕ» и «КОААНВ». Дешифрование выполняется, используя обратную перестановку.

Рассмотренные элементарные шифры подстановки и перестановки сами по себе не способны обеспечить требуемую в современных условиях стойкость криптографических систем, так как они уязвимы к атакам нарушителя на основе статистического анализа символов сообщений естественных языков, например таких, как телеграфные сообщения, написанные на русском языке. Однако, комбинируя элементарные шифры, можно построить широко используемые на

определяемая как f g(x)= f (g(x)) для всех x , принадлежащих множеству {X }.

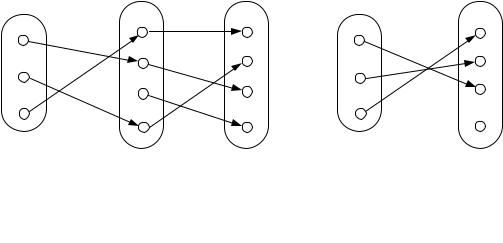
На рис. 10.7 показан пример композиции функций f и g . Композиция функций легко расширяется на случай произвольного числа функций, позволяя из элементарных функций шифрования синтезировать композиционные шифры с высокой стойкостью.

f g f g

В качестве элементарных шифрующих функцийудобно использовать инволюции, т. е., функции, у которых прямая функция совпадает с обратной к ней функцией. Использование инволюций позволяет существенно упростить построение блочных шифраторов и дешифраторов, так как композиционная функция шифрования совпадает с соответствующей функцией дешифрования.

428

дешифрования соответствующих исходных функций.

На практике удобно использовать подкласс композиционных шифров, называемый составными шифрами. В составных шифрах над блоком шифруемого сообщения многократно выполняются подстановки и перестановки. Последовательное использование подстановок и перестановок в составном шифре реализует два основных принципа построения симметричных блочных систем шифрования: рассеивание и перемешивание. Рассеивание заключается в распространении влияния всех символов блока открытого сообщения на все символы блока криптограммы, что позволяет скрыть статистические свойства шифруемой информации. Высокая степень рассеивания достигается многократными подстановками, зависящими не только от ключа, но и от промежуточных результатов шифрования. Одновременно рассеивание проявляется во влиянии каждого символа ключа на все символы блока криптограммы, что исключает восстановление взаимосвязи статистических свойств открытого и шифрованного текста. Перемешивание заключается в усложнении взаимосвязи статистических свойств сообщения и полученной из него криптограммы. Высокая степень перемешивания достигается при многократных перестановках в процессе криптопреобразований. Хорошее рассеивание и перемешивание обеспечивается использованием составного шифра, состоящего из последовательности элементарных шифрующих функций, каждая го которых вносит небольшой вклад в значительное суммарное рассеивание и перемешивание [1].

Современные составные шифры очень часто строятся как итеративные шифры, в которых над блоком сообщения многократно выполняется некоторый набор одних и тех же преобразований, называемых круговой функцией шифрования f . При выполнении каждой итерации круговой функции шифрования используется некоторая часть ключа шифрования, называемая подключом. Очередность выборки подключей из ключа шифрования называется расписани-

429

ем использования ключа шифрования. Итеративный процесс шифрования блока сообщения M можно записать в виде рекуррентной формулы:

C0 = x ,

Ci = f (Ci−1, K ), i =1,2,...,t ,

C = Ct ,

где Ci – значение блока криптограммы на i -й итерации шифрования; круго-

вая функция шифрования f отображает предыдущее значение блока крипто-

граммы Ci−1 под управлением подключа Ki в очередное значение блока крипто-

граммы Ci . Итоговое значение C определяется как значение блока крипто-

граммы Ct на последней итерации шифрования. В качестве начального значе-

ния криптограммы C0 используется значение блока сообщения x .

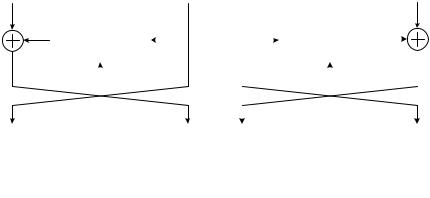
Итерационные блочные шифры вычислительно просто строить по схеме Фейстеля [1]. Для этого блоки сообщения и блоки криптограмм длиной по n бит разбиваются на левую L и правую R половины. Криптографическому преобразованию на каждой итерации шифрования подвергается только одна половина шифруемого сообщения; на следующей итерации половины меняются местами. Такой способ построения блочного шифра позволяет относительно просто при большом количестве итераций (циклов) обеспечить хорошее рас-

сеивание и перемешива-

следующей рекуррентной процедурой. Вначале производится разбиение блоков на левую и правую половины: (L0 , R0 )= x . Затем над правым полублоком выпол-

няются криптографические преобразования по круговой функции шифрования:

430