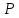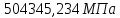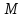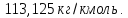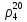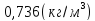- •Содержание:
- •1. Основные свойства битумов и методы их определения.
- •1.1 Битумы
- •1.2 Свойства битумов и методы их определения.
- •1.3 Применение и виды битумов.
- •2. Определение шифра коробковской нефти (бобриковский горизонт) по гост 38.1197-80 и гост р51858-2002.
- •Определение шифра нефти в соответствии с технологической классификацией.
- •Определение шифра нефти в соответствии с технической классификацией
- •3. Задачи Задача №1.
- •Задача №2
- •Задача №3
- •Задача №4
- •Задача №5
- •Задача №6
- •Задача №7
- •Задача №8
- •Задача №9
- •Задача №10
- •Приложения.
Задача №5
Найти абсолютную и относительную плотность газа при нормальных условиях (T_н=0℃=273 K,p_н=1 атм=101325 Па.), а также плотность этого газа при температуре t = 100°С и давлении Р = 0,8 МПа, зная массовый состав газа (% масс.).
Дано:
Таблица №8
|
Азот |
5 |
|
Углекислый газ |
1 |
|
Сероводород |
1 |
|
Метан |
74 |
|
Этан |
8 |
|
Пропан |
6 |
|
Изо-бутан |
2 |
|
Н-бутан |
2 |
I шаг
Молярная масса – величина аддитивная, и для смеси ее можно определить по формуле:
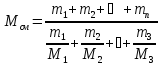
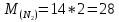 (кг/моль)
(кг/моль)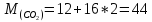 (кг/моль)
(кг/моль)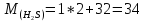 (кг/моль)
(кг/моль)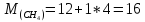 (кг/моль)
(кг/моль)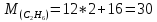 (кг/моль)
(кг/моль)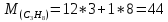 (кг/моль)
(кг/моль) (кг/моль)
(кг/моль) (кг/моль)
(кг/моль)
 (кг/моль)
(кг/моль)
II шаг
Относительная
плотность газа равна отношению массы
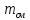 газа, занимающего объемV
при некоторой температуре и давлении,
к массе
газа, занимающего объемV
при некоторой температуре и давлении,
к массе
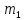 воздуха, занимающего тот же объемV
при тех же температуре и давлении. Если
считать газ идеальным, то при Т=273 К и
давлении Р = 1 атм. и V=22,4м3
масса m
равна молекулярной массе M
газа (
воздуха, занимающего тот же объемV
при тех же температуре и давлении. Если
считать газ идеальным, то при Т=273 К и
давлении Р = 1 атм. и V=22,4м3
масса m
равна молекулярной массе M
газа (
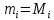 ).
).
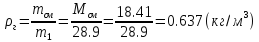
III шаг
Абсолютную плотность газов при нормальных условиях можно найти, зная массу M и объем 1 кмоль газа (22,4 м3), по формуле:

IV шаг
Плотность
газа при заданных условиях
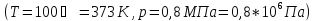 можно определить по формуле
Менделеева-Клапейрона:
можно определить по формуле
Менделеева-Клапейрона:

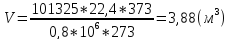
V шаг
Абсолютную
плотность газов при этих условиях можно
найти, зная массу
 :
:
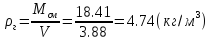
Ответ представлен в таблице №9
Таблица №9
|
|
0.637 |
|
|
0.823 |
|
|
4.74 |
Задача №6
Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения t1, °С. Определить давление насыщенных паров этой фракции при t2, °С, молярную массу и относительную плотность .
Дано:
Таблица №10
|
t1 ,°С |
125 |
|
t2 ,°С |
250 |
Решение:
I шаг
Для подсчета давления насыщенных паров узких нефтяных фракций при низких давлениях используют формулу Ашворта:
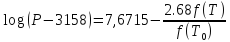
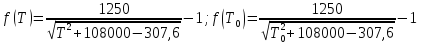
где P – давление насыщенных паров, МПа; T – температура кипения при давлении P, К; T0 – температура кипения при атмосферном давлении (для нефтяной фракции – средняя температура кипения), К;
Т=125°С=398 К
Т=250°С=523 К
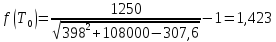
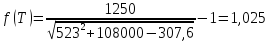
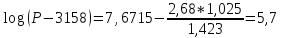
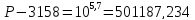
Следовательно:

II шаг
По формуле Войнова находят среднюю молярную массу:
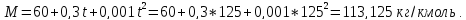
III шаг
Из
формулы Крэга выражается
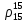 :
:
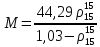
Следовательно:
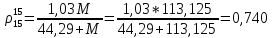
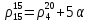
Следовательно:
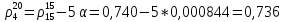
Ответ представлен в таблице №11
Таблица №11
|
|
|
|
|
|
|
|
|
Задача №7
Средняя температура кипения узкой бензиновой фракции при атмосферном давлении (≈1∙105 Па) составляет t1, °C. Найти ее температуру кипения t2, °C при давлении p2.
Дано:
Таблица №12
|
t1 , °С |
155 |
|
p2 , Па |
1.5*105 |
Решение:
Для решения можно использовать график Кокса (Приложение 6). График построен для воды и индивидуальных алканов нормального строения, но им широко пользуются и применительно к узким нефтяным фракциям. На графике Кокса находят точку с координатами, соответствующим известным давлению (Па) и температуре (К). Из найденной точки проводят равноудаленную от двух соседних лучей прямую до пересечения с вертикалью, соответствующей давлению, при котором необходимо найти температуру кипения. Из полученной точки проводят горизонталь, параллельную оси абсцисс, до пересечения с осью ординат, на которой получают точку, соответствующую искомой температуре.
Из номограммы следует что t2=444°K

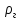 (абсолютная)
(абсолютная)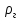 (относительная)
(относительная)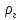 (при
t=100°C,
ρ=0,8 МПа)
(при
t=100°C,
ρ=0,8 МПа)