
Задача № 42
|
Масса изделия, г |
Число изделий, шт. |
x |
xf |
x
-
|
(x
-
|
(x
-
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
До 20 |
10 |
19,5 |
195 |
-1,9 |
3,61 |
36,10 |
|
20-21 |
20 |
20,5 |
410 |
-0,9 |
0,81 |
16,20 |
|
21-22 |
50 |
21,5 |
1075 |
0,1 |
0,01 |
0,5 |
|
22-23 |
15 |
22,5 |
337,5 |
1,1 |
1,21 |
18,15 |
|
Свыше 23 |
5 |
23,5 |
117,5 |
2,1 |
4,41 |
22,05 |
|
Итого |
100 |
- |
2135 |
- |
- |
93 |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение
3) коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которой ожидается средняя масса изделия всей партии изготовленных изделий;
5) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса изделий с массой выше 22 г.
Решение
1) Вычислить среднюю массу изделия:
Определим среднюю
массу изделия по выборке по формуле
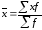
Следовательно,
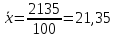

Таким образом, средняя масса одного изделия составляет 21,35 грамма.
2) Вычислить средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение:
Рассчитаем
выборочную дисперсию признака по формуле
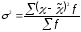 ,
где
,
где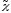 =21,35
=21,35
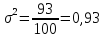
Рассчитаем среднее
квадратическое отклонение по формуле
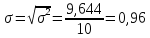
3) Вычислить коэффициент вариации:
Рассчитаем
коэффициент вариации по формуле
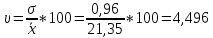
4) Вычислить с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которой ожидается средняя масса изделия всей партии изготовленных изделий:
Определим предельную
ошибку выборочной средней по формуле
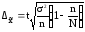 ,
где N
– объем генеральной совокупности, n
- объем выборочной совокупности (f),
t
– критерий достоверности ( при вероятности
0,954 t
= 2). По условию задачи количество
отобранных деталей составляет 10% от
общего количества, следовательно
,
где N
– объем генеральной совокупности, n
- объем выборочной совокупности (f),
t
– критерий достоверности ( при вероятности
0,954 t
= 2). По условию задачи количество
отобранных деталей составляет 10% от
общего количества, следовательно ,
отсюда
,
отсюда
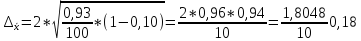
Возможная граница
генеральной средней определяется по
формуле:
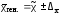 , следовательно
, следовательно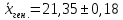 или 21,17
или 21,17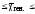 21,53
21,53
5) Вычислить с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса изделий с массой выше 22 г.
Предельная ошибка
выборочной доли определяется по формуле
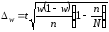 ,
где w
– выборочная доля (удельный вес единиц
в выборке, обладающих исследуемым
признаком w=m/n=22/100=0,22),
t
– критерий достоверности ( при вероятности
0,997 t
= 3)
,
где w
– выборочная доля (удельный вес единиц
в выборке, обладающих исследуемым
признаком w=m/n=22/100=0,22),
t
– критерий достоверности ( при вероятности
0,997 t
= 3)
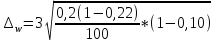 =3
=3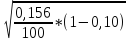 =
=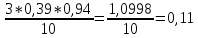
Возможная граница
генеральной доли определяется по
формуле:
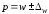
 ,
т.е. р=0,22+0,11
или 0,11
,
т.е. р=0,22+0,11
или 0,11 р
р 0,33
0,33
Ответ
1. Средняя масса изделия равна 21,35 грамма;
2. Дисперсия равна 0,93, среднее квадратическое отклонение равно 0,96;
3. Коэффициент вариации равен 4,496;
4. Предельная ошибка выборочной средней с вероятностью 0,954 равна 0,18, средняя масса изделия во всей партии изготовленных изделий ожидается в границах от 21,17 до 21,53;
5. Предельная ошибка выборочной доли с вероятностью 0,997 равна 0,11, границы удельного веса в общем объеме готовой продукции составят от 0,11 до 0,33.

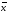 )2
)2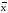 )2f
)2f