
- •Задачи математической статистики
- •Выборочный метод
- •Типы выборок и способы отбора.
- •Вариационные ряды
- •5. Эмперические функции распеделения
- •Полигон и гистограмма
- •Точечные оценки параметров распределения
- •Генеральная и выборочная средние.
- •Оценка генеральной дисперсии по исправленной выборочной дисперсии
- •Метод моментов для точной оценки параметров распределения
- •Доверительные интервалы для параметров нормального распределения.
- •Виды зависимости между случайными величинами
5. Эмперические функции распеделения
![]()
![]() Эмперической
функцией распределения наз. Функцию
(х), определяющего
для каждого значения х относительную
частоту события
Эмперической
функцией распределения наз. Функцию
(х), определяющего
для каждого значения х относительную
частоту события
В отличае от эмперичсекой функции распределения выборки функцию распр. Ген.сов. Назыв. Теорет. Функцией распред. Различае между ними состоит втом, что теоретич. Функция опрделяет вероятность события Х<х, а эмперическая относительную частоту этого же события.
Эфр служит для оценки теоретич. Функции распред. Ген. Совокупности.
При больших обьемах выборки значение теор.и эмпер. Функции распр.практически совпадают.
Свойства
-
Значение F*(х) принадлежит отрезку [0;1]
-
F*(х)-неубывающая функция
-
F*(х)=0, при х меньше x min, и F*(х)=1 при x больше x max
-
Полигон и гистограмма
Для нагладности стоят выриационные графики для различных рядов полигон для дискретных и гистограмм для вариациооных рядов.
Полигоном частот назыв.отрезки, которые соеденяют точкой [xi;ni]; а полигоном относительных частот 3 точки [xi ;wi]
Гистограммой назыв. Ступенчатая фигура стостоящая из прямоугольников, основаниями которых служат частичные интервалы (xi ;xi+1)длинной h, а высоты равны отношению ni и h.
![]() Гистограмма
относительных частот
Гистограмма
относительных частот
-
Точечные оценки параметров распределения
![]() Пусть
требуеться изучиь количественны признак
ген.совокупности. Допустим удалось
установить какое распределение имеет
признак. если нормальное то,...
Пусть
требуеться изучиь количественны признак
ген.совокупности. Допустим удалось
установить какое распределение имеет
признак. если нормальное то,...
![]() Статистической
оценкой неизвестного параметра нетеор.
Распр. Ген. Сов. Назыв. Функция
f(х1,х2,....хn)
Статистической
оценкой неизвестного параметра нетеор.
Распр. Ген. Сов. Назыв. Функция
f(х1,х2,....хn)
![]() Точесной
назыв. Статистич. Оценка, которая
характрериз. 1-м числом *f(х1,х2,....хn),
где х1,х2,....хn
результат n
наблюдений
над количественным признаком х
Точесной
назыв. Статистич. Оценка, которая
характрериз. 1-м числом *f(х1,х2,....хn),
где х1,х2,....хn
результат n
наблюдений
над количественным признаком х
К числу таких оценок относится например выборочное среднее и выборочная дисперсия.
Статистическая оценка является величиной и меняеться в зависимости от выборки.
![]() Несмещенная
Несмещенная
Смещенной Называеться точечная оценка мат ожид которой равно оцениваемому параметру.
-
Генеральная и выборочная средние.
Для характеристики среднего значения уоличественного признака Х в ген. Совок. Введено ген. Среднего.
![]() Генеральной
средней назыв. Среднее арифметическое
значений признака ген.совокупности.
Генеральной
средней назыв. Среднее арифметическое
значений признака ген.совокупности.
 1.
Если х1,х2,хn
в признаках ген. Сов. различны, то
1.
Если х1,х2,хn
в признаках ген. Сов. различны, то
-
 Если
значение повторяються
Если
значение повторяються
-
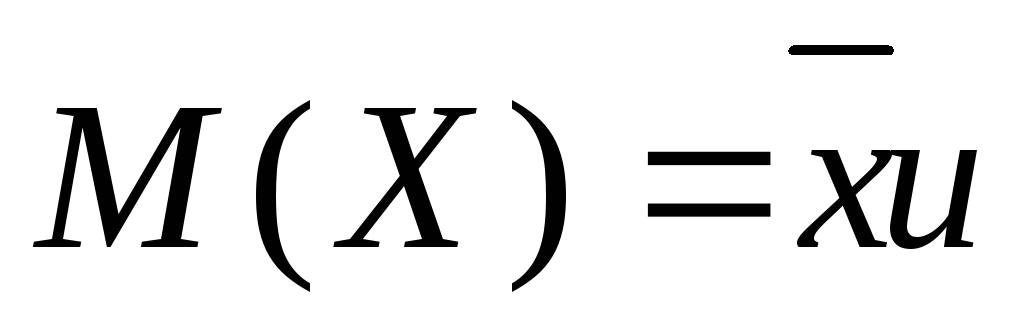 Если
рассматривать иследуемый признак Х в
ген. Совок. Как случайную велечину то
мат. Ожидание признака= ген.сред.этого
признака (опять не уверена)
Если
рассматривать иследуемый признак Х в
ген. Совок. Как случайную велечину то
мат. Ожидание признака= ген.сред.этого
признака (опять не уверена)
Выборочной средней назыв. Среднее арифметической значений придела выборочной совокупности.
-

-
( как 4, только к xi добавлено ni)
-
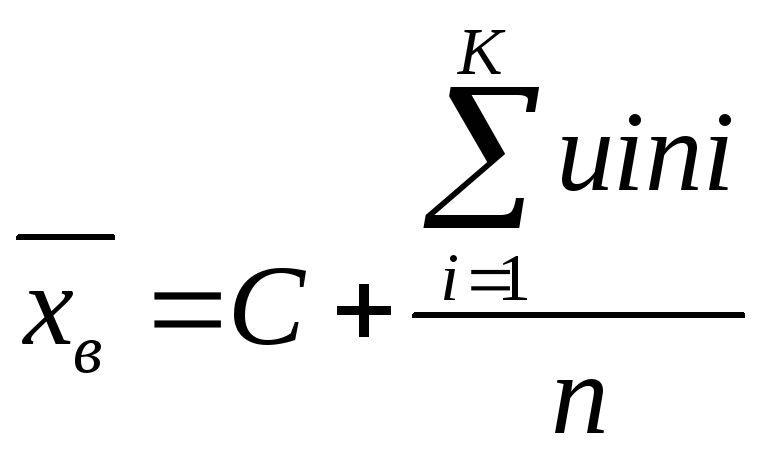
-
Генеральная и выборочная дисперсии
![]() генеральной
(Дг) называют среднее арифметической
квадратов отклонений значений призн.
Ген. Сов. От их среднего значения
генеральной
(Дг) называют среднее арифметической
квадратов отклонений значений призн.
Ген. Сов. От их среднего значения
-
 Если
все значения х1х2хn
признаки ген сов обьема N
различны, то
Если
все значения х1х2хn
признаки ген сов обьема N
различны, то
-
То же, только перед скобкой с х :Wi
Генеральным средним квадратичным отклонением назыв. Кв. Корень из дисперсии
![]()
