1. Понятие о земном эллипсоиде и сфере
Известно, что Земля шарообразна, т.е. не обладает формой идеального шара. Фигура ее неправильна, и, как всякое вращающееся тело, она немного сплюснута у полюсов. Кроме того, из-за неравномерного распределения масс земного вещества и тектонических деформаций Земля имеет обширные выпуклости и вогнутости. В силу этого земную поверхность заменяют некоторой правильной поверхностью, которая носит название поверхности относимости.
В самом точном приближении такой поверхностью является поверхность геоида (фигура, ограниченная уровенной поверхностью океана). Точно определить его форму практически невозможно. Поэтому в теории и практике картографии за поверхность относимости принимают земной эллипсоид, либо сферу определенного радиуса (при создании мелкомасштабных карт (когда можно пренебречь полярным сжатием).
Земной эллипсоид – это эллипсоид вращения с малым сжатием, размеры которого выбраны таким образом, чтобы для заданной территории он наименее уклонялся от геоида. При этом полагают, что плоскость экватора и центр эллипсоида вращения совпадают с плоскостью экватора и центром масс Земли. Такой земной эллипсоид иначе называют референц-эллипсоидом.
Постановлением Совета Министров от 7 апреля 1946 г. за такой референц-эллипсоид у нас в стране принят референц-эллипсоид Красовского. Он имеет следующие параметры:
a = 6 378 245 км – большая полуось;
b = 6 356 863 км – малая полуось;
с = 1 : 298,3 – полярное сжатие.
Рис.1. Эллипсоид вращения и его элементы
Эллипсоид вращения образуется вращением эллипса PNE1PSE2 вокруг полярной оси PNPS (рис. 1). Точки PN, PS являются, соответственно, северным и южным полюсами эллипсоида. Они получаются сечением оси PNPS поверхности эллипсоида.
Сечения поверхности эллипсоида вращения плоскостями, параллельными плоскости экватора, образуют окружности – параллели. Сечения поверхности эллипсоида вращения плоскостями, проходящими через ось вращения, образуют эллипсы – меридианы.
Пусть О'К' – нормаль к поверхности эллипсоида в точке К (рис. 1). Плоскости, проходящие через нормаль, называются нормальными плоскостями. Сечения этих плоскостей с поверхностью эллипсоида дают нормальные сечения, или вертикалы. Тогда меридиан – это нормальное сечение, плоскость которого проходит через полярную ось. Нормальное сечение, перпендикулярное плоскости меридиана PNЕ1PSЕ2, дает сечение 1-го вертикала.
Радиусы кривизны этих сечений определяются следующими формулами:
–радиус кривизны
меридиана;
–радиус кривизны
1-го вертикала;
где 
– 1-й эксцентриситет;
a и b – большая и малая полуоси эллипсоида вращения.
Радиус параллели (r) вычисляется через радиус кривизны первого вертикала
2. Система координат на поверхности эллипсоида и сферы
Положение точки на поверхности эллипсоида может быть определено в той или иной системе координат. Основная система координат – географическая с φ, λ (рис. 2).
Рис. 2. Система географических координат на эллипсоиде вращения
Географическая широта (φ) есть угол между плоскостью экватора и нормалью ОМ (отвесная линия) текущей точки М (рис. 2). Широта меняется от 0 до 90°.
Географическая долгота (λ) есть двугранный угол между плоскостями начального меридиана и меридиана текущей точки М. Долгота изменяется от 0 до 180° на запад и восток от начального меридиана. При картографических расчетах западные долготы берутся со знаком «минус», восточные – со знаком «плюс».
Кроме рассмотренной системы координат, существует целый ряд других, используемых в математической картографии:
- прямоугольная сфероидическая;
- сферическая полярная и др.
Под координатными линиями следует понимать геометрические места точек, для которых одна из координат постоянна. Например, параллель есть геометрическое место точек равных широт (φ = const), а меридиан есть геометрическое место точек равных долгот (λ = const).
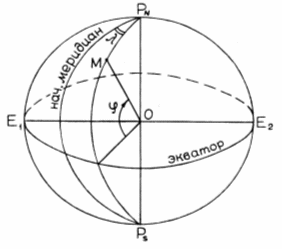
Рис. 3. Система географических координат на сфере
В тех случаях, когда Земля принимается за сферу, географическими координатами называют сферические координаты φ, λ с полюсом системы координат, совпадающим с географическим полюсом (рис. 3).