2 Цепи с трансформаторами

Трансформатор используется для преобразования токов и напряжений, развязки и согласования отдельных участков цепи. Он состоит из двух или нескольких индуктивно связанных обмоток или катушек.

Рассмотрим работу трансформатора в синусоидальном режиме. Для его схемы замещения (рисунок 12) запишем уравнения по второму закону Кирхгофа в комплексной форме ( токи направлены согласно одноименным клеммам катушек)

где – комплексное сопротивление нагрузки трансформатора.

Перепишем уравнения:

где . Объединив уравнения, получим

.

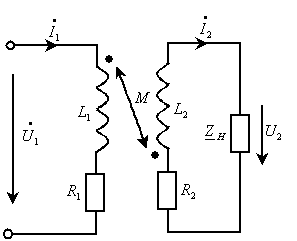
Рисунок 12 –схема замещения трансформатора

Следовательно, комплексное входное сопротивление всей цепи равно

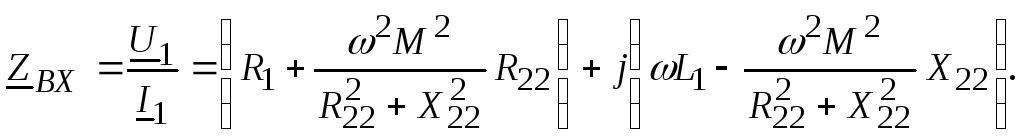
Выделим действительную и мнимую составляющие , гдегде

Составляющие иназывают, соответственно, вносимым активным и вносимым реактивным сопротивлениями. Вносимые сопротивления представляют собой такие сопротивления, которые следовало бы «внести» в первичную цепь (включить последовательно сR₁ и X₁), чтобы учесть влияние нагрузки вторичной цепи трансформатора на ток в его первичной цепи.

Рассмотрим свойства трансформаторов в предельных идеализированных случаях. Предположим, что и

Тогда

Трансформатор, для которого соблюдается условие при любой нагрузке, называется совершенным трансформатором (n – коэффициент трансформации). Если принять (практическиL₁ должно иметь достаточно большое значение, чтобы можно было пренебречь составляющей тока по сравнению с), то между токами и напряжениями на первичной и вторичной обмотках трансформатора имеют место соотношения:

Трансформатор, для которого соблюдаются эти условия, называется идеальным трансформатором. Такой трансформатор обладает свойством изменять токи и напряжения независимо от значения сопротивления, включенного во вторичный контур, в определенное число раз. Для идеального трансформатора получим

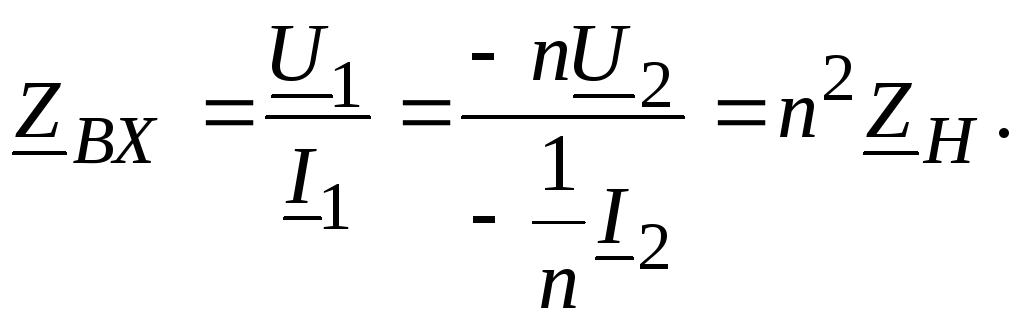
При помощи идеального трансформатора можно произвести также и изменение сопротивления в определенное число раз, не зависящее от характера этого сопротивления.

Схема замещения входного сопротивления реального нагруженного трансформатора в общем случае представляет резистивное и индуктивное сопротивления, соединенные параллельно (рисунок 13). Индуктивная составляющая обуславливается током намагничивания, а резистивная – сопротивлением нагрузки и резистивным сопротивлением обмоток.

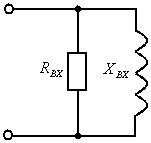
Рисунок 13 – схема замещения входного сопротивления трансформатора

Приблизить характеристики трансформатора к идеальным можно за счет использования сердечника из ферромагнитного материала: сплавов на основе железа, никеля, магнитодиэлектриков – ферритов. Трансформаторы с ферромагнитными сердечниками при этом являются нелинейными элементами электрических цепей, но эта нелинейность незначительно влияет на соотношения между первичными, вторичными токами и напряжениями. Это позволяет использовать соотношения, полученные для линейного трансформатора, с поправочными коэффициентами.

В идеальных трансформаторах намагничивающий ток мал, и сопротивление – бесконечно велико. В этом случае оказывается, что при нагрузке трансформатора на резистивный элементR_Н входное сопротивление является чисто резистивным и определяется из выражения

,

где R₂ – резистивное сопротивление вторичной обмотки трансформатора.

В совершенном трансформаторе индуктивная проводимость имеет конечное значение, но если , то реактивной составляющей можно пренебречь и считать входное сопротивление трансформатора чисто резистивным.

Чтобы экспериментально измерить входное сопротивление трансформатора, необходимо знать действующее значения напряженияи токана первичной обмотке трансформатора и фазовый угол между ними. В этом случае резистивная составляющая входного тока определяется из выражения , а реактивная составляющая. Сопротивления:,.