
- •Методические указания
- •Лабораторная работа №3
- •Аппаратура и материалы
- •Указания по технике безопасности
- •Методика и порядок выполнения работы
- •1 Исследование токораспределения в цепи с параллельным соединением катушки индуктивности и конденсатора при различных величинах емкости конденсатора
- •2 Исследование частотных характеристик цепи с параллельным соединением r, l и с элементов
- •Содержание отчета и его форма
- •Задание 3
- •Форма отчета
- •Контрольные вопросы и защита лабораторной работы
- •Лабораторная работа №4
- •2 Цепи с трансформаторами
- •Аппаратура и материалы
- •Указания по технике безопасности
- •Методика и порядок выполнения работы
- •1 Экспериментальное определение взаимной индуктивности м и коэффициента связи k между катушками
- •2 Исследование токораспределения в цепи с индуктивно связанными катушками
- •3 Исследование различных режимов работы трансформатора
- •Содержание отчета и его форма
- •Контрольные вопросы и защита лабораторной работы
- •Литература Основная учебная литература
- •Дополнительная литература
- •Методические указания
- •355029, Г. Ставрополь, пр.Кулакова, 2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
СЕВЕРО-КАВКАЗСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Методические указания
к выполнению лабораторных работ
по дисциплине “Теоретические основы электротехники”
для студентов специальностей:
140205 (100200) «Электроэнергетические системы и сети»,
140211 (100400) «Электроснабжение»,
210104 (200100) «Электроника и микроэлектроника»,
210106 (200400) «Промышленная электроника»
Ставрополь 2005
Методические указания к выполнению лабораторных работ составлены в соответствии с требованиями ГОСВПО, рабочих учебных планов специальностей: 140205 (100200) – электроэнергетические системы и сети, 140211 (100400) – электроснабжение, 10104 (200100) – электроника и микроэлектроника, 210104 (200400) – промышленная электроника и программ дисциплины «Теоретические основы электротехники».
Предназначены для студентов всех форм обучения.
Составители: В.М. Кожевников, Ю.А. Ларионов, Т.Ф.Морозова,
И.Ю. Чуенкова
Рецензент: Гринь А.И.
Содержание:
Лабораторная работа №3
Цель и содержание………………………………………………………4
Теоретическое обоснование…………………………………………….4
Аппаратура и материалы………………………………………………..10
Указания по технике безопасности…………………………………….12
Методика и порядок выполнения работы……………………………...13
Содержание отчета и его форма………………………………………...17
Контрольные вопросы и защита работы……………………………….20
Лабораторная работа №4
Цель и содержание………………………………………………………22
Теоретическое обоснование……………………………………………..22
Аппаратура и материалы…………………………………………………29
Указания по технике безопасности……………………………………...30
Методика и порядок выполнения работы……………………………….34
Содержание отчета и его форма …………………………………….......34
Контрольные вопросы и защита работы………………………………...38
Литература…………………………………………………………….…..39
Лабораторная работа №3
«Исследование явления резонанса при параллельном соединении
участков цепи с R, L и С элементами»
Цель и содержание
Цель работы: Экспериментально исследовать режимы работы цепи с параллельным соединением участков цепи, содержащих R, L и С элементы, в том числе режима «резонанса токов».
Для достижения цели необходимо:
1. Исследовать токораспределение в цепи с параллельным соединением катушки индуктивности и конденсатора при различных величинах емкости конденсатора. Определить условие резонанса в параллельной цепи.
2. Исследовать частотные характеристики цепи с параллельным соединением R, L и С элементов.
Теоретическое обоснование
В качестве критерия режима резонанса в электрических цепях, содержащих катушки индуктивности и конденсаторы, принимается совпадение по фазе тока и напряжения на входных зажимах, т.е. фазовый резонанс. Ток совпадает по фазе с напряжением, если входное реактивное сопротивление или входная реактивная проводимость всей цепи оказываются равными нулю. Возможны два основных типа резонанса: при последовательном соединении катушки индуктивности и конденсатора – резонанс напряжений и при их параллельном соединении – резонанс токов.
А. Резонанс напряжений. Резонанс напряжений возможен на неразветвленном участке электрической цепи, который содержит индуктивный L, емкостной С и резистивный R элементы, т.е. в последовательном колебательном контуре (рисунок 1).
Рисунок 1 – Последовательный колебательный контур
По закону Ома комплексная величина тока в контуре определяется
![]() ,
,
где
![]() – комплексное входное сопротивление,
– комплексное входное сопротивление,![]() – его модуль (полное сопротивление),
– его модуль (полное сопротивление),
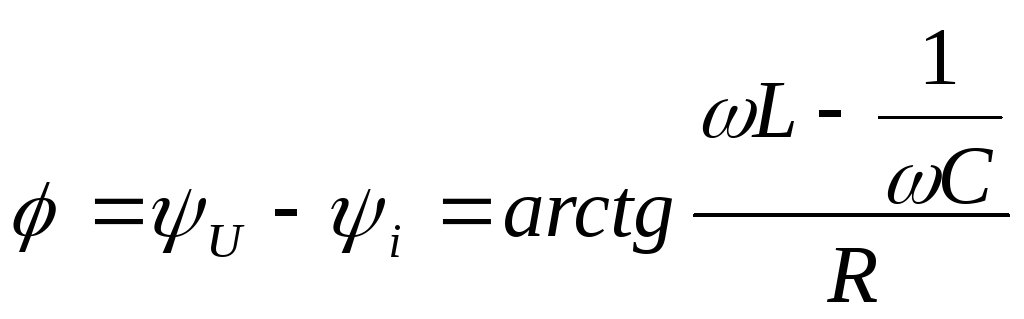 – его аргумент.
– его аргумент.
Действующее
значение тока:
 .
.
Режим работы неразветвленного участка
цепи, при котором ее ток и напряжение
совпадают по фазе
![]() ,
,![]() ,
называется резонансом напряжений. В
режиме резонанса напряжение на емкостном
и напряжение на индуктивном элементах
равны и находятся в противофазе (рисунок
2).
,
называется резонансом напряжений. В
режиме резонанса напряжение на емкостном
и напряжение на индуктивном элементах
равны и находятся в противофазе (рисунок
2).
Рисунок 2 – Векторная диаграмма при резонансе напряжений
Резонансного
режима можно достичь, изменяя частоту
приложенного к цепи напряжения или
параметры цепи: индуктивность катушки
и емкость конденсатора. Величины угловой
частоты![]() ,
индуктивностиLo
и емкости Co,
в резонансном режиме:
,
индуктивностиLo
и емкости Co,
в резонансном режиме:
![]()
Если
напряжение U
на зажимах
цепи и активное сопротивление R
цепи не изменяются, то ток при резонансе
имеет наибольшее значение, равное
![]() и не зависящее от величин реактивных
сопротивлений. Напряжения на емкостном
и индуктивном элементах могут во много
раз превысить напряжение питания, если
и не зависящее от величин реактивных
сопротивлений. Напряжения на емкостном
и индуктивном элементах могут во много
раз превысить напряжение питания, если![]() ,
где
,
где![]() -
характеристическое (волновое) сопротивление
колебательного контура. Отношение
-
характеристическое (волновое) сопротивление
колебательного контура. Отношение![]() определяет кратность превышения
напряжения на зажимах индуктивного и
емкостного элементов над напряжением
питания и называется добротностью
контура.
определяет кратность превышения
напряжения на зажимах индуктивного и
емкостного элементов над напряжением
питания и называется добротностью
контура.
Практическое значение имеют зависимости действующих или амплитудных значений токов и напряжений от частоты для цепей, в которых возможен резонанс. Эти зависимости называются резонансными кривыми (рисунок 3).

Рисунок 3 – Резонансные кривые
Для
оценки избирательных свойств электрической
цепи введено понятие ширины резонансной
кривой или полосы пропускания контура,
которую определяют как разность верхней
ωВ
и нижней ωН
частотами, между которыми
![]() .
Чем выше добротностьQ,
тем уже полоса пропускания контура.
.
Чем выше добротностьQ,
тем уже полоса пропускания контура.
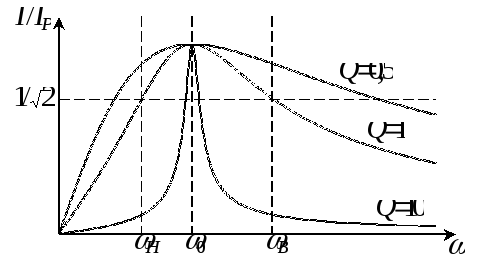
Рисунок 4 – Полоса пропускания контура
Б.
Резонанс токов. Резонанс
токов может
возникнуть в параллельном колебательном
контуре (рисунок 5). При напряжении
питания
![]() комплексное значение общего тока будет
равно:
комплексное значение общего тока будет
равно:

Рисунок 5 – Параллельный колебательный контур
![]() ,
,
где
![]() – комплексная проводимость цепи;
– комплексная проводимость цепи;![]() – ее модуль (полная проводимость) и
– ее модуль (полная проводимость) и - аргумент. Действующее значение тока
- аргумент. Действующее значение тока![]() .
.
При угловой частоте
![]() индуктивная
индуктивная
![]() и емкостная
и емкостная![]() проводимости ветвей одинаковы
проводимости ветвей одинаковы![]() ,
угол сдвига фаз тока и напряжения
,
угол сдвига фаз тока и напряжения![]() ,
т.е.
,
т.е.![]() .
Полбольшее значениеная проводимость
активная
.
Полбольшее значениеная проводимость
активная![]() ,
и общий ток
,
и общий ток![]() .
Если напряжениеU
на зажимах цепи активная проводимость
g
цепи не изменяются, то общий ток при
резонансе имеет наименьшее значение.
Токи в индуктивном и емкостном элементах
равны по величине и находятся в
противофазе. (рисунок 6).
.
Если напряжениеU
на зажимах цепи активная проводимость
g
цепи не изменяются, то общий ток при
резонансе имеет наименьшее значение.
Токи в индуктивном и емкостном элементах
равны по величине и находятся в
противофазе. (рисунок 6).

Рисунок 6 Векторная диаграмм при резонансе токов
Если в ветвях с индуктивным и емкостным элементами включены резисторы RL и RC, то условием резонанса токов в цепи будет равенство индуктивной и емкостной проводимостей ветвей (рисунок 7):
 ,
резонансная частота
,
резонансная частота .
.
.
.
Если
RC=0,
то резонанс
наступает при :
![]() (рисунок 8).
(рисунок 8).
Добротность
для параллельного контура
![]() определяет кратность превышения тока
в индуктивном и емкостном элементах
над общим током при резонансе, где RЭКВ
– эквивалентное сопротивление
определяет кратность превышения тока
в индуктивном и емкостном элементах
над общим током при резонансе, где RЭКВ
– эквивалентное сопротивление
![]() ;
;![]() - волновая проводимость.
- волновая проводимость.
Резонансные
свойства контура характеризуют также
величиной, носящей название затухание
контура
![]() .
.

Рисунок 7 – Колебательный контур с потерями

Рисунок 8 – Колебательный контур и векторная диаграмма при RC=0
