chisl_meth / Лаб 5 Задача на собственные значения / Метод Крылова, Данилевского

Метод Крылова

Суть метода Крылова состоит в преобразовании матрицы

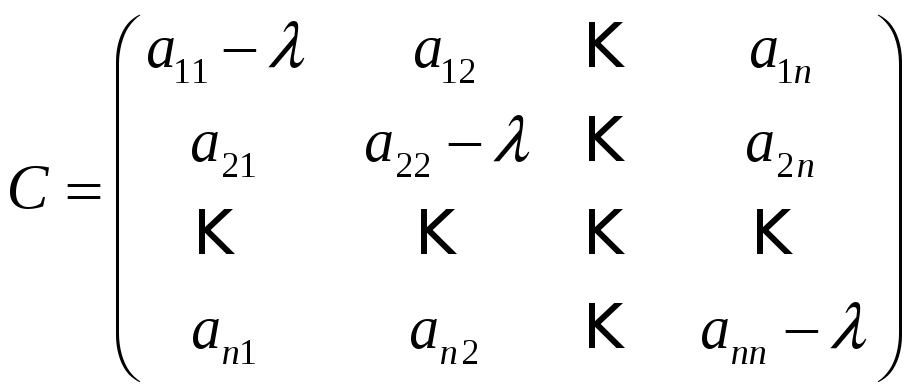(1)

к эквивалентной матрице вида

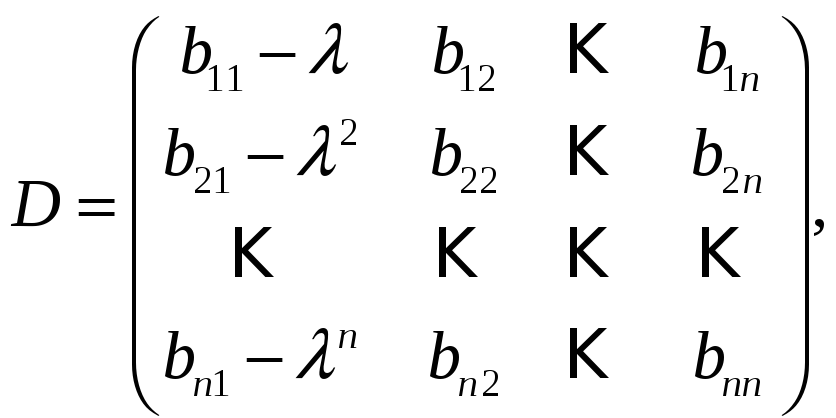(2)

развертывание которого по степеням осуществляется значительно проще, при помощи разложения определителя по минорам 1-го столбца.

Перепишем (1) в виде

(3)

Преобразуем систему следующим образом. Умножим первое уравнение на и заменим их выражениями (3) через Получим

(4)

где

Умножим далее уравнение (4) на и заменим снова их выражениями через

Повторяя этот процесс раз, мы перейдем от системы (3) к системе

(5)

коэффициенты которой будут определяться по рекуррентным формулам

Определитель системы (5) будет иметь тот же вид, что и определитель матрицы (2). Теперь мы можем записать характеристическое уравнение, при помощи которого и определяются собственные значения.

С другой стороны, чтобы получить характеристическое уравнение, можно свести задачу к нахождению коэффициентов характеристического уравнения из системы вида

где векторы определяются равенствами , а

Например, для нахождения собственных чисел матрицы размерностью необходимо последовательно вычислить вектора

, , , ,

после этого составить систему линейных алгебраических уравнений для нахождения коэффициентов характеристического полинома:

а затем составить его и найти собственные значения одним из методов решения нелинейного уравнения:

Собственные вектора можно определить следующим образом:

где коэффициенты вычисляются по схеме Горнера: