chisl_meth / Лаб 7 Интерполяция / Интерполирование 1

Интерполирование

Линейная и квадратичная интерполяции

Простейшим и часто используемым видом локальной интерполяции является линейная (или кусочно линейная) интерполяция. Она состоит в том, что заданные точки соединяются прямолинейными отрезками, и функция приближается ломаной с вершинами в данных точках.

Для каждого интервала в качестве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки:

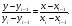
Отсюда

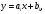
Рассмотрим теперь случай квадратичной интерполяции. В качестве интерполяционной функции на отрезке 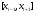принимается квадратный трехчлен. Такую интерполяцию называют также параболической.

Уравнение квадратного трехчлена

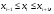
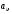
содержит три неизвестных коэффициента 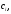для определения которых необходимы три уравнения. Ими служат условия прохождения параболы через три точки Эти условия можно записать в виде

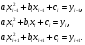
Пример. Найти приближенное значение функци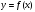и при с помощью формул линейной и квадратичной интерполяций, если известна следующая таблица ее значений:

x	0.15	0.30	0.40	0.55
y	2.17	3.63	5.07	7.78

Многочлен Лагранжа

Обратимся к случаю глобальной интерполяции, т. е. к построению интерполяционного многочлена, единого для всего отрезка Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n:

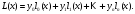
При этом потребуем, чтобы каждый многочлен обращался в нуль во всех узлах интерполяции, за исключением одного (i-го), где он должен равняться единице. Этим условиям при 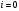отвечает многочлен вида

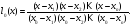
По аналогии можно записать

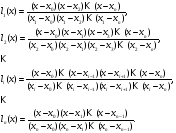
Подставляя последние выражения в многочлен степени n, находим

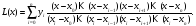
Эта формула определяет интерполяционный многочлен Лагранжа. Из нее можно получить выражения для линейной и квадратичной интерполяции.

Многочлен Ньютона

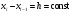
Рассмотрим случай равноотстоящих значений аргумента, т. е. 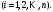Величина h называется шагом. Введем также понятие конечных разностей.

Пусть известны значения функции в узлах 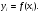Составим разности значений функции:

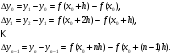
Эти значения называются первыми разностями (или разностями первого порядка) функции.

Можно составить вторые разности функции:

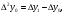
Аналогично составляются разности порядка k:

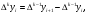
Конечные разности можно выразить непосредственно через значения функции. Например,

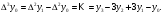
Аналогично для любого k можно написать

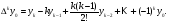
Эту формулу можно записать и для значения разности в узле

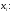
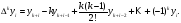
Используя конечные разности, можно определить

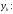
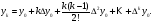
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде:

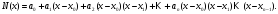
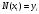
График многочлена должен проходить через заданные узлы, т. е. 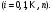Эти условия используем для нахождения коэффициентов многочлена:

Найдем отсюда коэффициенты

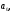
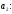
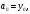
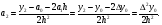
Аналогично можно найти и другие коэффициенты. Общая формула имеет вид

Подставляя эти выражения в многочлен получаем следующий вид интерполяционного многочлена Ньютона:

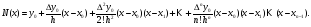
Конечные разности 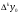могут быть вычислены по формуле записанной выше.

Последнее выражение часто записывают в другом виде. Для этого вводится переменная 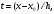тогда

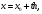
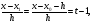
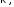
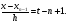
С учетом этих соотношений формулу интерполяционный многочлен Ньютона можно переписать в виде

Полученное выражение называется первым интерполяционным многочленом Ньютона для интерполирования вперед. Оно может аппроксимировать данную функцию 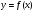на всем отрезке изменения аргумента Однако с точки зрения повышения точности расчетов (путем уменьшения погрешностей округления) более целесообразно использовать полученную формулу для вычисления значении функции в точках левой половины рассматриваемого отрезка.

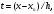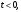Для правой половины отрезка разности лучше вычислять справа налево. В этом случае т. е. и интерполяционный многочлен Ньютона можно получить в виде

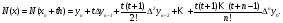
Полученная формула называется вторым интерполяционным многочленом Ньютона для интерполирования назад.

Пример. Вычислить в точке 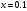значение функции 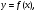заданной табл.

Таблица

x	y
0	1.272
0.2	4.465
0.4	5.644
0.6	5.809
0.8	3.961
1.0	2.101