Фово Лекции

дисперсии. Это волокно оптимально для случая передачи одной длины волны - одноканальной передачи. Однако волокно DSF имеет ограниченные возможности при использованиях в системах многоканального волнового мультиплексирования WDM. При передаче многоканального сигнала используются эрбиевые оптические усилители. Оказалось, что именно длина волны нулевой дисперсии 1550 нм, попадая внутрь рабочего диапазона эрбиевого усилителя, является источником нелинейных эффектов (прежде всего, четырехволнового смешивания), что проявляется в резком возрастании шума при распространении многоканального сигнала.

Для преодоления недостатков волокна DSF, проявляющихся при работе с мультиплексным оптическим сигналом, было создано волокно с ненулевой смещенной дисперсией NZDSF. Длина волны нулевой дисперсии такого волокна вынесена за пределы полосы пропускания эрбиевого усилителя. Это уменьшает нелинейные эффекты и улучшает характеристики волокна при передаче WDM сигнала.

Выводы

Рассмотрены механизмы возникновения потерь в оптических волокнах, способы их уменьшения и оптимальные рабочие длины волн для оптического волокна.

Вопросы и задачи

12.1.Ознакомьтесь с видами потерь в оптическом волокне. Чем определяются потери в длинноволновой области? Какие примеси приводят с увеличению потерь вблизи длины волны 1480 нм?

12.2.Что такое рэлеевское рассеяние?

12.3.Чем определяются кабельные потери?

12.4.Что такое длина отсечки волокна?

12.5.Какие рабочие диапазоны длин волн вы можете назвать? Для каких длин волн оптимизированы современные оптические волокна, применяемые в высокоскоростных сетях?

111

ЛЕКЦИЯ 13 Источники излучения для оптической связи.

Излучение света в p-n – переходе. 13.1. Источники излучения

Оптический источник для оптоволоконной системы связи должен удовлетворять нескольким основным требованиям:

•источник должен иметь высокую выходную яркость в узкой полосе частот на требуемой длине волны в 850 нм, 1310 нм, 1550 нм,

•выходное излучение должно легко модулироваться,

•площадь излучающей поверхности не должна быть больше сердцевины волокна,

•угловое распределение излучения должно быть согласовано с волокном,

•источник должен иметь высокий КПД, большую надежность и стабильность выходной мощности,

•стоимость производства источника должна быть относительно невысокой.

Внастоящее время используются два основных типа источника, удовлетворяющие данным требованиям: светодиоды и полупроводниковые лазерные диоды.

13.2.Собственные и примесные полупроводники

Опишем свойства полупроводниковых материалов, которые

могут быть использованы для генерации света. Читатель, знакомый с зонной теорией твердого тела, данный раздел может пропустить.

Рассмотрим зонную диаграмму собственных полупроводников (без примесей). В собственных полупроводниках при температуре абсолютного нуля валентная зона (ВЗ) полностью заполнена электронами, зона проводимости (ЗП) пуста (см. рис. 13.1, а). Между валентной зоной и зоной проводимости находится запрещенная зона (ЗЗ), в которой отсутствуют разрешенные энергетические уровни электронов. Если сообщить электронам валентной зоны энергию, равную ширине запрещенной зоны, они могут перейти из валентной зоны в зону проводимо-

112

сти. При этом в валентной зоне образуются пустые уровни, которые можно интерпретировать как положительно заряженные дырки. Ширина запрещенной зоны в полупроводниках достаточно велика (она достигает нескольких электроновольт). Поэтому в собственных полупроводниках при сообщении дополнительной энергии (например, при росте температуры) переходы электронов из ВЗ в ЗП происходят редко. Значит, собственная проводимость полупроводников очень мала.

Рис. 13.1. Зонная диаграмма полупроводников. а) - собственный полупроводник, б) - донорный полупроводник, в) - акцепторный полупроводник.

На рис. 13.1. Ec - дно зоны проводимости, E v - потолок валентной зоны, EF - энергия уровня Ферми. Под уровнем Ферми

для полупроводников будем понимать уровень, вероятность заполнения которого равна 0,5. В собственном полупроводнике уровень Ферми находится посередине запрещенной зоны.

Рассмотрим донорный полупроводник или полупроводник n-типа - полупроводник, в который введена примесь, с валентностью, на единицу большей валентности основного материала. С точки зрения зонной теории при введении донорной примеси внутри запрещенной зоны появляются дополнительные уровни, заполненные электронами (рис.13.1,б). При соответствующем выборе примеси эти уровни находятся ближе к зоне проводимости. При росте температуры электроны с донорных уровней лег-

113

ко переходят в зону проводимости. Таким образом, в донорных полупроводниках имеются основные носители - электроны зоны проводимости, и также неосновные носители - дырки в валентной зоне, возникшие из-за наличия у полупроводника собственной проводимости.

В акцепторный полупроводник или полупроводник р-типа введена примесь с валентностью на единицу меньшей валентности основного материала. С точки зрения зонной теории при введении акцепторной примеси внутри запрещенной зоны появляются дополнительные незаполненные уровни (рис.13.1,в). При росте температуры электроны валентной зоны легко переходят на эти акцепторные уровни, при этом в валентной зоне образуются дырки, являющиеся основными носителями. Неосновными носителями в полупроводнике р-типа являются электроны зоны проводимости, возникшие из-за наличия собственной проводимости.

13.3. p-n - переход

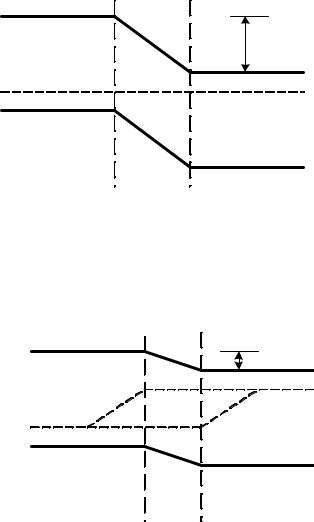
Рассмотрим диаграмму энергетических уровней p-n - перехода, находящегося в равновесном состоянии. Напомним, что в полупроводнике n-типа уровень Ферми смещен от середины запрещенной зоны в сторону зоны проводимости, а в полупроводнике р-типа - в сторону валентной зоны (см. рис. 13.1, б), в)). В равновесном состоянии p-n - перехода, то есть в отсутствие внешнего напряжения, уровень Ферми будет одинаков в облас-

тях n- и p- типа (рис. 13.2).

Наличие потенциального барьера величиной qU0 мешает

электронам зоны проводимости переходить из област-и n в область р-типа.

На рисунке 13.3 изображена диаграмма энергетических уровней p-n - перехода при прямом включении (к переходу приложено напряжение U). При этом состояние термодинамического равновесия нарушается, и вместо уровня Ферми необходимо использовать понятие квазиуровней Ферми: EF n - квазиуровень

Ферми для электронов, EF p - квазиуровень Ферми для дырок.

114

Ec

Рис. 13.2. Диаграмма энергетических уровней p-n - перехода в равновесном состоянии. Ec - нижний уровень зоны проводимо-

сти, E v - верхний уровень валентной зоны, qU0 - величина потенциального барьера..

EFn

EFp

Ev

Ev

Рис. 13.3. Диаграмма энергетических уровней p-n - перехода при прямом включении.

115

Подача прямого напряжения U приводит к смещению квазиуровней Ферми относительно равновесного положения и к уменьшению высоты потенциального барьера до величины q(U0 − U) . Снижение высоты потенциального барьера позволя-

ет основным носителям пересекать область p-n - перехода, создавая значительный ток. Таким образом, электроны из зоны проводимости n- области инжектируются в зону проводимости р-области, дырки инжектируются из области р- в область n- типа.

13.4.Инжекционная люминесценция

Врезультате включения p-n - перехода в прямом направлении наблюдается значительный ток, созданный основными носителями, и происходит рекомбинация электронов и дырок. Рекомбинация в p-n - переходе может сопровождаться несколькими независимыми конкурирующими процессами. Для нас важны различия между излучательными и безызлучательными процессами рекомбинации. При безызлучательных переходах освободившаяся в результате рекомбинации энергия идет на нагревание полупроводника. При излучательной рекомбинации энергия рекомбинации преобразуется в энергию излученного кванта света.

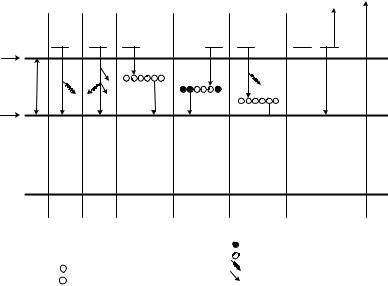
На рисунке 13.4 схематически изображены несколько процессов рекомбинации. Наибольший интерес для нас представляет прямой зона-зонный излучательный переход (рис. 13.4, а), при котором и происходит излучение кванта света на рабочей частоте. Основные конкурирующие безызлучательные переходы идут через глубоко лежащие в запрещенной зоне ловушечные уровни (рис. 13.4, в, г). Даже если при таких переходах с участием ловушечных уровней происходит излучение светового кванта, частота его сильно отличается от рабочей частоты. Причиной появления этих ловушечных уровней могут быть примесные атомы или дефекты кристаллической решетки, которые в большом количестве встречаются на поверхности полупроводника.

116

Рис. 13.4. Механизмы электронно-дырочной рекомбинации (в каждом случае отдельные стадии процесса следуют слева направо) а) - прямой зона-зонный излучательный переход; б) - излучательный зона-зонный переход с участием одного или нескольких фононов энергии E′ ; в) - переходы (возможно, безызлучательные) с участием глубоких акцепторных ловушек; г) - переходы (возможно, безызлучательные) с участием глубокого донорного уровня; д) переходы (излучательные или безызлучательные) с участием неглубокого акцепторного уровня; е) - безызлучательный "сверлящий" рекомбинационный переход.

13.5. Спектры рекомбинационного излучения

Энергия кванта света, рождающегося в результате рекомбинации, то есть в результате перехода электрона с уровня с энергией E2 на уровень с энергией E1 , определяется по формуле:

Чтобы выяснить распределение энергии рекомбинационного излучения по энергиям, проведем следующее рассуждение [1].

117

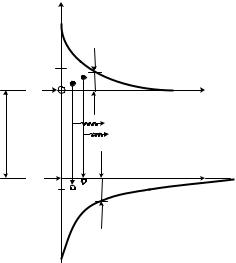
Вероятность рекомбинации электрона с энергией E2 и дырки с энергией E1 пропорциональна произведению n(E2 ) p(E1 ) , где n(E2 ) - концентрация электронов на уровне с энергией E2 , p(E1 ) - концентрация дырок с энергией E1 . Вероятность излучения фотона с энергией Eф может быть найдена в результате интегрирования произведения n(E2 ) p(E1 ) по всем значениям E2 . Таким образом, спектральная плотность мощности излучения может быть найдена следующим образом:

E1

Рис. 13.5. Упрощенный вид функций распределения электронов и дырок в соответствии с (13.3) и (13.4).

Концентрация электронов на уровне с энергией E2 пропор-

циональна функции распределения Ферми-Дирака, аналогично с использованием функции распределения Ферми-Дирака можно найти и концентрацию дырок. Однако для наших вычислений можно воспользоваться некоторыми упрощениями. Будем считать, что концентрация свободных электронов экспоненциально

118

уменьшается с удалением энергии электрона E2 от нижнего

Аналогично, концентрация дырок экспоненциально уменьшается при удалении энергии дырки E1 от верхнего края валентной

Здесь А и В - некоторые константы.

Тогда спектральная плотность мощности излучения

Здесь коэффициенты А и В заменены коэффициентом К, в который входят вероятность перехода и радиационное время жизни электронов. Таким образом

= K(Eф − Eg ) exp[− Eф − Eg ] , kT

где Eg = Ec − E v - ширина запрещенной зоны.

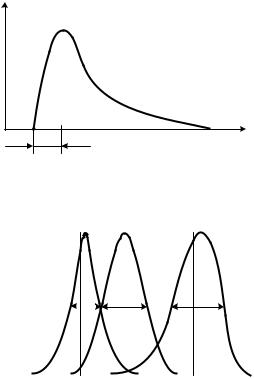
В результате приведенного анализа получаем, что теоретически рассчитанное спектральное распределение мощности рекомбинационного излучения имеет вид рис. 13.6. Наблюдаемый спектр всегда выглядит более симметрично (см. рис. 13.7).

119

Рис. 13.6. Спектральное распределение мощности излучении, рассчитанное по формуле (13.6).

Рис. 13.7. Наблюдаемый спектр излучения диодов на основе InGaAsP трех различных составов [1].

Искажение наблюдаемого спектра излучения по сравнению

стеоретическим определяется рядом обстоятельств. Во-первых, в светоизлучающих диодах и лазерах обычно используются высокие концентрации донорных и акцепторных примесей, что вызывает искажение края запрещенной зоны. Во-вторых, наряду

сизлучением фотона может происходить взаимодействие с кристаллической решеткой. В таком случае часть энергии рекомбинации может передаваться фонону, который является квантом упругих колебаний кристаллической решетки. В-третьих, переход может идти в несколько этапов с участием одного из примесных уровней вблизи края зоны.

120