
Fizika_Ekzamen_vip
.pdf
Сдаем физику за 1 семестр.
1)Механическое движение. Кинематика М.Т. Траектория, перемещение, мгновенная и средняя скорость, ускорение точки.
Механика занимается изучением законов движения и взаимодействия тел.
Механическое движение: изменение положения тела в пространстве относительно других тел с течением времени.
Кинематика изучает законы движения тел без учета сил, вызывающих это движение.
М.Т. - тело, размером и формой которого можно пренебречь(размер<<расстояния).
С.О.- система координат, снабженная часами и жестко связанная с абсолютно твердым телом.
Абсолютно твердое тело - тело, деформации которого равны нулю.
Траектория М.Т. - линия, описываемая этой точкой при её движении относительно выбранной системы координат.
Перемещение - изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта.
Вектор перемещения - вектор, проведенный из начального положения точки в момент t1 в положение в момент t2.
Скорость - векторная величина, которая вводится для характеристики быстроты и направления движения.
Мгновенная скорость в момент времени t называется v вектор , равный первой производной по времени от радиус-вектора этой точки.
Мгновенная скорость есть касательная к траектории в данный момент времени.
! |
! |
r = dr |
v = lim |
< v >= lim |
|
t→∞ |
t→∞ |
t dt |
Средняя путевая скорость - скалящая величина, равная отношению изменения пути за к
A t протяженности промежутка.
< v >= s1 + s2 + ... + sn t1 + t2 + ... + tn
Средняя скорость точки - векторная величина, равная отношению перемещения точки за A t к длительности этого интервала.
< ! >= r = r2 − r1 v
t t
! |
= |
v = |
Ускорение - векторная величина, которая характеризует изменение скорости по величине и направлению.
! |
= |
a = |
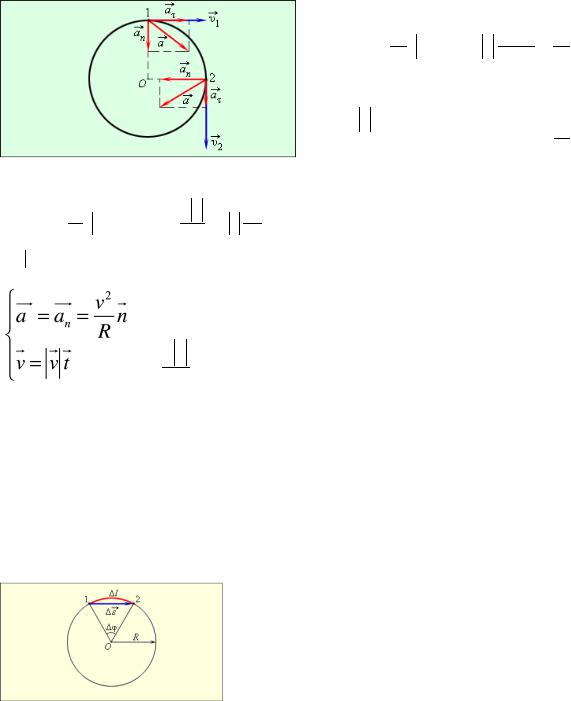
2)Произвольное криволинейное движение М.Т. Нормальная и тангенциальная составляющая ускорения. Движение точки по кругу.
При произвольном криволинейном движении материальной точки полное ускорение a может быть разложено на две составляющие: an и aτ , где an aτ .
Тангенциальная - модуль, нормальная - направление.
Вектор полного ускорения характеризует изменение скорости по величине и направлению и направлен внутрь кривизны траектории.
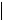 a
a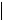 =
= 
!"! |
|
" |
d |
" |
|
|
|
dv |
|
||||
an |
= |
dt |
= dt v(t) *τ (t) |
= |
||
" |
|
|
! |
|
|
|
v = v(t) *τ (t) |
|
|
|
|||
|
|
|
|
!"! |
|
dv |
d |
|
" |
|
! dτ (t) |
v2 |
! |
||
|
|
|
|
an = |
|
|
|
= v |
dt |
= R n |
|||||
|
|
|
|
dt = dt v τ (t) |
|||||||||||
|
|
|
|
! |
! ! |
- касательная, тау - единичный |
|||||||||
|
|
|
|
v = v τ |
|||||||||||
|
|
|
|
dτ |
|
! |
вектор касательной |
|
|
|
|||||
|
|
|
|
= |
v |
|
|
|
|
!"! |
!"! |
= v |
2 |
" |
|
|
|
|
|
dt |
R |
|
|
|
|
aц |
= an |
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|||
d v |
! ! |
! |
!"! |
!"! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
τ + v dτ |
= aτ |
+ an |
|
|
|
|
|
|
|
|
|
|
|
||
dt |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
!"! |
= d v |
! |
aτ |
τ |
|
|
dt |
|
Движение точки по кругу.
Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения s удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах. Длина дуги связана с углом поворота
соотношением
l = R ϕ
При малых углах поворота l = s.
Линейное и угловое перемещения при движении тела по окружности.
Угловой скоростью ω тела в данной точке круговой траектории называют предел (при t → 0) отношения
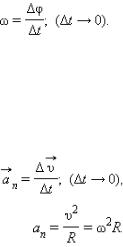
малого углового перемещения Δφ к малому промежутку времени t:
A
Угловая скорость измеряется в рад/с.
Связь между модулем линейной скорости v и угловой скоростью ω: v = ωR.
При равномерном движении тела по окружности величины v и ω остаются неизменными. В этом случае при движении изменяется только направление вектора v .
Равномерное движение тела по окружности является движением с ускорением. Ускорение направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением.
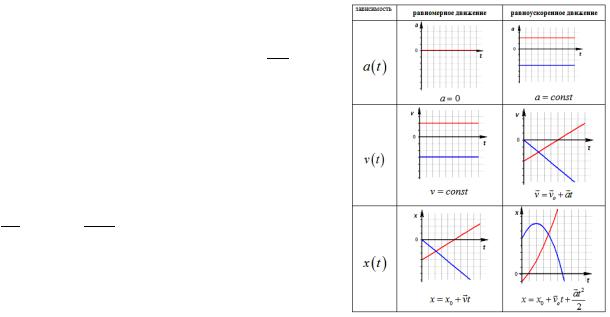
3)Прямолинейное движение. Равномерное и равноускоренное движение.
Прямолинейное движение - движение, при котором траектория представляет собой прямую линию.
Прямолинейным равномерным движением называется механическое движение, при котором тело за любые равные промежутки времени.
Скорость прямолинейного равномерного движения - это векторная физическая величина, численно равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Равномерное движение - v = const x = x0 + vxt
Равноускоренное движение x = x + v t + at 2
0 x
2
Ускорение - первая производная по скорости и вторая по координате.
a = lim |
v = dv = v' |
|||
t→0 |
t |
|
dt |
|
|
" |
|
= d |
2 " |
a = d dr |
|
r |
||
dt dt |
|
dt 2 |
||
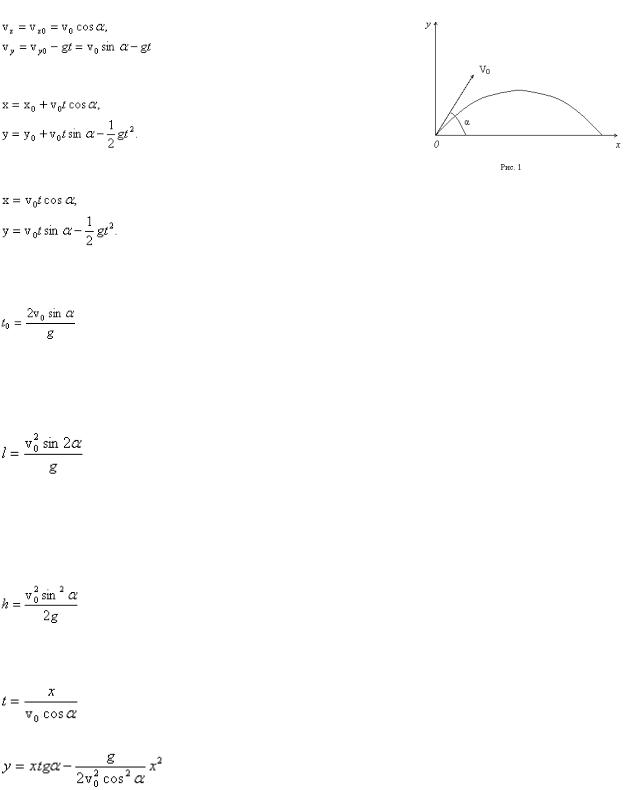
4)Движение тела, брошенного под углом к горизонту. Максимальная высота подъема, время и дальность полета.
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
A |
, |
Координаты тела, следовательно, изменяются так:
A
При нашем выборе начала координат начальные координаты равны нулю.
A (1)
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
A.(2)
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:
A |
.(3) |
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
A |
.(4) |
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
A
и подставить его во второе уравнение. Тогда получим:
A |
. |

5)Плоскопараллельное движение твердого тела. Переносное и относительное движение.
Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости.
Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге.
Здесь плоскопараллельное движение в каждый момент времени может быть представлено в виде суммы двух движений —
полюса C, являющегося не чем иным, как центром вращения колеса в связанной с ним системе координат (в общем случае по любой траектории на плоскости с точки зрения неподвижного наблюдателя) и вращательного движения остальных точек тела вокруг этого центра.
В таком случае вектор абсолютной скорости движения любой точки будет определяться векторной суммой переносной скорости движения центра вращения С, (одинаковой для расчёта скорости любой точки колеса). И вектора относительной скорости выбранной точки, зависящей от её положения, угловой скорости вращения и расстояния от центра.
Если в данный момент для точки контакта колеса с поверхностью (точки А) эти скорости равны по модулю и противоположны по направлению, имеет место случай чистого (без проскальзывания) качения, что показано на рисунке. Только в этом случае скорость точки М будет в 2 раза больше скорости точки С и направлена в ту же сторону.
Относительное, переносное и абсолютное движения.
До сих пор мы изучали движение точки или тела по отношению к одной заданной системе отсчета. Однако в ряде случаев при решении задач механики оказывается целесообразным (а иногда и необходимым) рассматривать движение точки (или тела)
одновременно по отношению к двум системам отсчета, из которых одна считается основной или условно неподвижной, а другая определенным образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют составным или сложным. Например, шар, катящийся по палубе движущегося парохода, можно считать совершающим по отношению к берегу сложное движение, состоящее из качения по отношению к палубе (подвижная система отсчета), и движение вместе с палубой парохода по отношению к берегу (неподвижная система отсчета). Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых.
Рис.1
Рассмотрим точку М, движущуюся по отношению к подвижно системе отсчета Oxyz, которая в свою очередь как-то движется относительно другой системы отсчета O1x1y1z1, которую называем основной или условно неподвижной (рис.1). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным. Введем следующие определения.
1. Движение, совершаемое точкой М по отношению к подвижной системе отсчета (к осям Oxyz), называется относительным движением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относительной траекторией. Скорость точки М по отношению к осям Oxyz называется относительной

скоростью A , a ускорение - относительным ускорениемA . Из определения следует, что
при вычислении A и A можно движение осей Oxyz во внимание не принимать (рассматривать их как неподвижные).
2. Движение, совершаемое подвижной системой отсчета Oxyz (и всеми неизменно связанными с нею точками пространства) по отношению к неподвижной системе O1x1y1z1, является для точки М переносным движением.
Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной
скоростью точки М в этот момент (обозначаетсяA |
), а ускорение этой точки m - |
переносным ускорением точки М (обозначается A |
). Таким образом,A |
A
Если представить себе, что относительное движение точки происходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.
3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета O1x1y1z1, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекторией, скорость - абсолютной скоростью (обозначается
A ) и ускорение - абсолютным ускорением (обозначаетсяA ).
Вприведенном выше примере движение шара относительно палубы парохода будет относительным, а скорость - относительной скоростью шара; движение парохода по отношению к берегу будет для шара переносным движением, а скорость той точки палубы, которой в данный момент времени касается шар будет в этот момент его переносной скоростью; наконец, движение шара по отношению к берегу будет его абсолютным движением, а скорость - абсолютной скоростью шара.
При исследовании сложного движения точки полезно применять «Правило остановки». Для того, чтобы неподвижный наблюдатель увидел относительное движение точки, надо остановить переносное движение.
Тогда будет происходить только относительное движение. Относительное движение станет абсолютным. И наоборот, если остановить относительное движение, переносное станет абсолютным и неподвижный наблюдатель увидит только это переносное движение.
Впоследнем случае, при определении переносного движения точки, обнаруживается одно очень важное обстоятельство. Переносное движение точки зависит от того в какой момент будет остановлено относительное движение, от того, где точка находится на среде в этот момент. Так как, вообще говоря, все точки среды движутся по-разному. Поэтому логичнее определять переносное движение точки как абсолютное
движение той точки среды, с которой совпадает в данный момент движущаяся точка.

6)Кинематика вращательного движения твердого тела вокруг неподвижной оси. Величины, характеризующие вращательное движение твердого тела.
Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения.
Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' .
Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr.
При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой
точки твердого тела, ни первая производная A , ни вторая производная A не могут
служить характеристикой движения всего твердого тела.
За это же время dt радиус-вектор A , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться).
Угол поворота dφ характеризует перемещение всего тела за время dt.
Удобно ввести A – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели
вращение по часовой стрелке (направление вектора A и направление вращения связаны «правилом буравчика»).
Элементарные повороты удовлетворяют обычному правилу сложения векторов:
A
Угловой скоростью называется вектор A , численно равный первой производной от
угла поворота по времени и направленный вдоль оси вращения в направлении A
( A и A всегда направлены в одну сторону).
A |
ω = |
ϕ ,(t →0) |
. (2.4.1) |
t |
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси. Пусть v – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время dr = Rdφ (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой:
A |
(2.4.2) |
|
В векторной форме A |
. |
|
Вектор A |
ортогонален к векторам A и A и направлен в ту же сторону, что и |
|
векторное произведение A |
. |
|
Наряду с угловой скоростью вращения используют понятия периода и частоты
вращения.
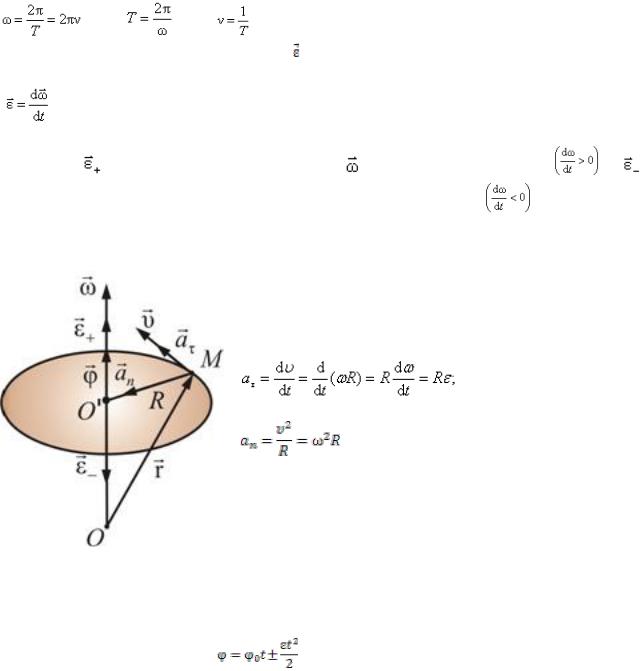
Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π).
Частота ν – число оборотов тела за 1 секунду. При вращении с угловой скоростью ω имеем:
A |
, |
A |
, |
A |
. |
Введем вектор углового ускорения A для характеристики неравномерного вращения тела:
A(2.4.3)
Вектор A направлен в ту же сторону, что и A при ускоренном вращении A |
, а A |
|
направлен в противоположную сторону при замедленном вращении A |
(рис. 2.13). |
|
Как и любая точка твердого тела, точка М имеет
нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
A
aτ = Rε; (2.4.4)
A |
(2.4.5) |
Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения.
Формулы простейших случаев вращения тела вокруг неподвижной оси:
равномерное вращение ε = 0; |
ω = const; |
φ = φ0 ± ωt, |
равнопеременное вращение A |
. |
|
7)Инерциальные системы отсчёта. Первый закон Ньютона. Силы в природе.
Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.
Системы отсчета, в которых выполняется 1-й закон Ньютона, называются
инерциальными системами отсчета.
Все системы отсчета, движущиеся прямолинейно и равномерно относительно данной инерциальной системы отсчета, тоже являются инерциальными.
Системы отсчета, движущиеся относительно любой инерциальной системы отсчета с ускорением, являются неинерциальными.
Первый закон Ньютона: Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.
Сила - количественная мера взаимодействия одного тела на другое.
Для задания силы необходимо указать модуль, направление и точку приложения.
Классификация сил:
1.Гравитационные силы [10-38]
•сила тяготения
Все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
.
Коэффициент пропорциональности G называется гравитационной постоянной,
G = 6,67*10-11(Н*м2)/кг2.
• сила тяжести
Сила тяжести - сила притяжения, которая действует на тело на поверхности Земли.
P = mg
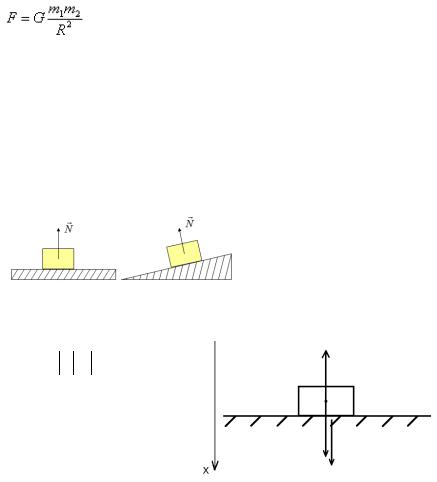
• сила реакции опоры
Сила реакции опоры - сила, действующая на тело со стороны опоры или подвеса. Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
• вес тела Вес тела - сила, с которой тело действует на опору или подвес.
G - вес тела |
!" !" !" |
|
N |
|
" |
!" |
= 0 |
||
a = 0 |
→ P = |
G , P + N |
||
OX /P − N = 0 → P = N
Из III з.Н. → N = G
G
P = mg
При ускорении, направленном вверх G = P + ma вниз G = P − ma
a = g → G = 0
