Для популяции размножающихся половым путем диплоидных организмов есть два шага в переносе частот генотипов в одном поколении в частоты генотипов следующего поколения

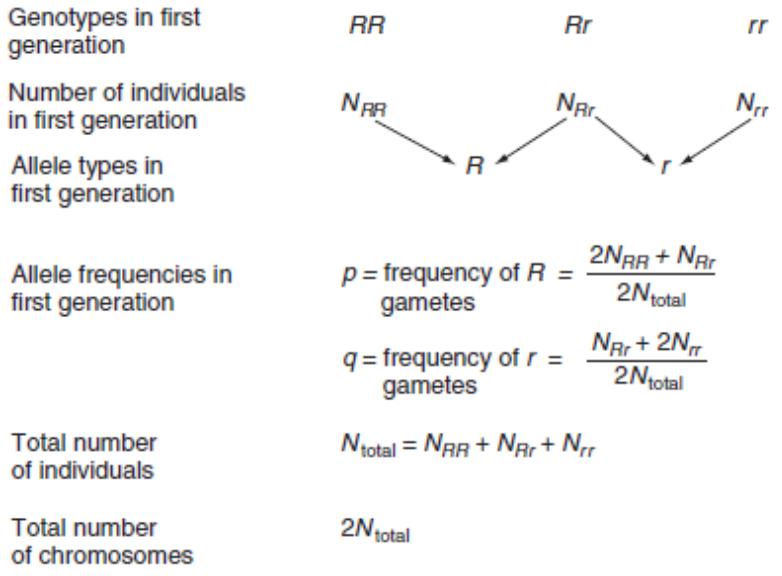
Для популяции в равновесии Харди-Вайнберга, частоты генотипов могут быть рассчитаны из частот аллелей с использованием законов Менделя о

распределении аллелей и простой вероятности. Здесь частота аллеля A 0.7, и частота аллеля a 0.3. Частоты генотипов в следующем поколении:

AA: 0.49 aa: 0.09

Aa: 0.21 x 2 = 0.42

При равновесии Харди-Вайнберга, частоты аллелей в

следующем поколении должны остаться постоянными. Например, частота аллеля A должна быть 0.49 + (0.5 x 0.42) = 0.7.

Какова будет частота аллелей в генофонде нового поколения при размножении этих выросших зигот?

Генотипы АА составят 49% генофонда, Аа - 42%. аа – 9%. Частота аллеля А в новом генофонде составит 0.49 + 0.21 = 0.7, а - 0.09 + 0.21 = 0.3, т.е. частоты аллелей не меняются при смене поколений.

В общем случае p2 + 2pq + q2 = 1

Популяции, в которых частоты аллелей не меняются из поколения в поколение, а частоты генотипов можно предсказать, исходя из частот аллелей, находятся в состоянии равновесия Харди-Вайнберга.

Следствия закона Харди-Вайнберга

1) доминантные признаки совсем не обязательно встречаются чаще в последующих поколениях,

2)в популяции может поддерживаться генетическая изменчивость, т.к. частоты аллелей не меняются,

3)можно рассчитать частоты всех генотипов, исходя из частот одного.

Тесты на равновесие

Для проверки, нарушаются ли условия закона Харди-Вайнберга, нужно определить, находятся ли генотипы данной популяции в состоянии равновесия. Для этого нужно определить частоты генотипов либо по фенотипам, либо анализом белков и ДНК. После этого можно рассчитать частоты аллелей из частот генотипов.

Проверка хи-квадрат, где число степеней свободы определяется как к – 1 – м,

где к - число генотипов, м -число независимых частот аллелей, оцененных исходя из имеющихся данных.

Для случая p2 + 2pq + q2 = 1 к = 3, м = 1 (поскольку расчет частоты аллеля возможен через расчет другого, т.е. степеней свободы 1).

Если тест показал, что популяция не в состоянии равновесия – значит, одно или несколько условий не выполняются

Если в популяции 283 человека, из которых 223 имеют генотип 1/1, 57 – генотип 1/Δ32 и 3 – генотип Δ32/Δ32.

Эти числа соответствуют частотам генотипов

223/283 = 0.788, 57/283 = 0.201 и 3/283 = 0.011. Исходя из частот генотипов, частота аллеля CCR51 = 0.89 и аллеля CCR5-Δ32 = 0.11.

Используя данные частоты аллелей и закон Харди-Вайнберга, можно определить, находится ли популяция в состоянии равновесия.

Данные частоты аллелей дадут следующие ожидаемые частоты генотипов

Частота генотипа 1/1 = p2 = (0.89)2 = 0.792 Частота генотипа 1/Δ32 = 2pq = 2 х 0.89 х 0.11 = 0.196 Частота генотипа Δ32/Δ32 = q2 = (0.11)2 = 0.012

Представленные частоты крайне близки к наблюдаемым, следовательно, нет свидетельств нарушения условий равновесия Харди-Вайнберга. Вывод можно подтвердить анализом по критерию хи-квадрат

Расширение закона Харди-Вайнберга

Нередко в одном локусе несколько аллелей, например группы крови , тогда p+q+r = 1, (p+q+r)2 = p2 + q2 + r2 + 2pq + 2pr + 2qr = 1

Если в популяции частоты групп крови А = 0.53, В = 0.13, АВ = 0.08, 0 = 0.26. Аллель О – рецессивный, поэтому частота группы О равна доле рецессивных генотипов r2, тогда r = 0.51.

Используя это значение, можно оценить частоты аллелей А и В.

Для А - частота АА равна p2, АО - 2pr.

Суммарная встречаемость групп А и О = 0.53 + 0.26, тогда (p+r)2 = 0.79, откуда р = 0.89 – r = 0.38.

Частота В = q = 1 - 0.38 - 0.51 = 0.11

Из этого частоты генотипов АА – 0.14, АО – 0.39, ВВ – 0.01, ВО – 0.11, АВ – 0.084, ОО – 0.26

Применение закона Харди-Вайнберга – расчет частоты гетерозигот

Одно из применений закона Харди-Вайнберга – оценка частоты гетерозигот в популяции.

Оценка проводится на основе частоты рецессивного признака (его обычно можно подсчитать по числу особей с ним в выборке) и закона Харди-Вайнберга.

Если частота признака 0.004, то q = 0.02, p = 0.98 и, следовательно, 2pq = 0.04, т.е. частота гетерозигот 4%.

Можно определить и частоты всех трех генотипов. В популяциях, для которых p и q заключены между 0.33 и 0.67, гетерозиготы встречаются чаще, чем доминантные и рецессивные гомозиготы.