Сортировка Шелла

Представляет собой сортировку с помощью прямого включения путем уменьшения расстояния.

Сортировка Шелла является довольно интересной модификацией алгоритма сортировки прямого включения.

Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

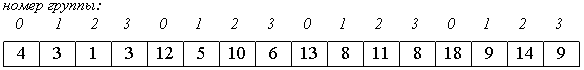
В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

4. В конце сортируем вставками все 16 элементов.

Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?

Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.

Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.

Использованный в примере набор ..., 8, 4, 2, 1 — неплохой выбор, особенно, когда количество элементов — степень двойки. Однако гораздо лучший вариант предложил Р. Седжвик. Его последовательность имеет вид

.

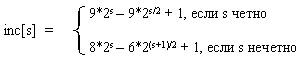При использовании таких приращений среднее количество операций: O(n^7/6), в худшем случае - порядка O(n^4/3).

Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке.

При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.

int increment(long inc[], long size) {

Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size.

Рассмотрим простейший пример реализации сортировки Шелла для расстояний 4–2–1 для числового массива a

0,57

0,48

34,27

0,05

-0,11

-24,00

Массив следует отсортировать по возрастанию.

Алгоритм сортировки имеет вид

1. Задать массив расстояний h.

2. Реализовать сортировку с помощью прямого включения для h=4, предусмотрев блокировку выхода за пределы массива.

3. Выполнить шаг 2 для h=2 и h=1.

4. Определить общее число перестановок элементов массива.

Результаты сортировки приведены ниже

Исходный массив
0,57	0,48	34,27	0,05	-0,11	-24,00

Отсортированный массив
-24,00	-0,11	0,05	0,57	0,48	34,27

Результаты сортировки						Расстояние
-0,11	-24,00	34,27	0,05	0,57	0,48	h = 4

-0,11

-24,00

0,57

0,05

34,27

0,48

h = 2

-24,00

-0,11

0,05

0,57

0,48

34,27

h =1

Число перестановок = 6

Программный код, реализующий сортировку Шелла по возрастанию:

Sub Sort_Shell()

'сортировка Шелла

'с помощью прямого включения путем

'уменьшения расстояния по возрастанию

Const Nk% = 9

Dim a!(1 To 25), i%, n%, m%, j%, s!, s1!, k%

Dim h%(1 To 5), l%

n = 1 ' размерность массива

'считывание данных из таблицы

While Cells(2, n) <> ""

a(n) = Cells(2, n)

n = n + 1

Wend

n = n - 1

' проверка считанных данных

'For i = 1 To n

' Cells(4, i) = a(i)

'Next i

' сортировка эл-тов массива по убыванию

h(1) = 4: h(2) = 2: h(3) = 1

m = 0 ' число перестановок

For j = 1 To 3

For i = 1 To n

k = h(j)

If a(i) > a(i + k) Then

If i + k > n Then Exit For ' предотвращение выхода

s = a(i) ' за пределы массива

a(i) = a(i + k)

a(i + k) = s

m = m + 1

End If

Next i

' вывод результатов проходов

' For i = 1 To n

' Cells(8, i) = a(i)

' Cells(8, i).NumberFormat = "0.00"

' Next i

'

Next j

For i = 1 To n

Cells(4, i) = a(i)

Cells(4, i).Font.Italic = True 'оформление ячеек вывода

Cells(4, i).Font.Bold = True ' стилем

Cells(4, i).NumberFormat = "0.00" 'вывод данных в заданном формате

Cells(4, i).Font.Color = RGB(45, 255, 123)

Next i

Cells(9, 1) = "Число перестановок = " & m

End Sub

Sub CommandButton1_Click()

Sort_Shell

End Sub

Пример реализации приведенного алгоритма сортировки по убыванию показан ниже

Исходный массив
0,57	0,48	34,27	0,05	-0,11	-24,00

Отсортированный массив
34,27	0,57	0,48	0,05	-0,11	-24,00

Пример сортировки Шелла символьного массива

Исходный массив
йцу	qwe	rty	123,00	cvb	мит

Отсортированный массив
мит	йцу	rty	qwe	cvb	123,00

Реализована на основе Вирт (с. 100) и не ориентирована на определенную последовательность расстояний. Все расстояния t обозначаются через h₁, h₂,… , h_t и для них справедливо условие:

h_t =1, h_i+1<h_i.

Каждая h-сортировка реализуется как сортировка с помощью прямого включения, причем простота условий окончания поиска места для включения обеспечивается методом барьеров. Ясно, что каждая из сортировок нуждается в в постановке своего барьера и программу для определения его местоположения следует делать как можно более простой. Поэтому массив расширяется на не на одну компоненту а₀, а на h₁ компонент.

Пример сортировки Шелла с изменяющимся расстоянием показан ниже

Исходный массив
0,57	0,48	34,27	0,05	-0,11	-24,00

Отсортированный массив
-24,00	-0,11	0,05	0,48	0,57	34,27

Пример кода на языке Visual Basic

Sub Sort_Shell3()

'сортировка Шелла

'с помощью прямого включения путем

'уменьшения расстояния

Const Nk% = 9

Dim a!(-9 To 25), i%, n%, m%, j%, s%, s1!, k%

Dim h%(1 To 5), l%

n = 1 ' размерность массива

'считывание данных из таблицы

While Cells(2, n) <> ""

a(n) = Cells(2, n)

n = n + 1

Wend

n = n - 1

' проверка считанных данных

'For i = 1 To n

' Cells(4, i) = a(i)

'Next i

' сортировка эл-тов массива по убыванию

h(1) = 3: h(2) = 1:

For m = 1 To 2

k = h(m)

s = -k

For i = k + 1 To n

s1 = a(i): j = i - k

If s = 0 Then s = -k

s = s + 1: a(s) = s1

While s1 < a(j)

a(j + k) = a(j)

j = j - k

Wend

a(j + k) = s1

Next i

' вывод результатов проходов

'For l = 1 To n

' Cells(9, l) = a(l)

' Cells(9, l).NumberFormat = "0.00"

'Next l

'

Next m

For i = 1 To n

Cells(4, i) = a(i)

Cells(4, i).Font.Italic = True 'оформление ячеек вывода

Cells(4, i).Font.Bold = True ' стилем

Cells(4, i).NumberFormat = "0.00" 'вывод данных в заданном формате

Cells(4, i).Font.Color = RGB(45, 255, 123)

Next i

End Sub