
- •Содержание
- •Введение
- •Библиографический список
- •1. Организационно-экономическая сущность задачи
- •1.1. Понятия производственной программы предприятия
- •1.2. Оптимизация производственной программы
- •2. Математическая постановка задачи и метод её решения
- •2.1. Формализация задачи
- •2.2. Метод решения
- •2.3. Алгоритм решения задачи
- •2.4. Решение задачи. Вариант №2
2.3. Алгоритм решения задачи
Последовательность вычислений при решении задачи оптимизации, поставленной в п. 2.1., сводится к следующему.
Находим
координаты (

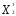 )
точки
)
точки - встречи линии пересечения плоскостей
ограничений и координатой плоскости
- встречи линии пересечения плоскостей
ограничений и координатой плоскости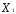 =
0, решая систему уравнений:
=
0, решая систему уравнений:

 +
+

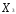 =
= ;
;
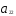
 +
+

 =
=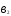 .
.
Поскольку
векторы ( ,
, ),
(
),
( ,
,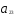 )
линейно независимы, решение существует
и может быть представлено в виде:
)
линейно независимы, решение существует
и может быть представлено в виде:
 = 0;
= 0;
 =
= ;
; =
= .
.
Проверяем
выполнение предположения о неотрицательных
объемах производства. Если хотя бы одно
из найденных решений отрицательно, т.е.
 <
0 или
<
0 или <
0, точка
<
0, точка = (
= (
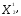
 )
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю,
)
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю, =
0. В противном случае следует найти
значение целевой функции в этой точке:
=
0. В противном случае следует найти
значение целевой функции в этой точке:
 =
=

 +
+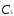
 .
.
Находим
координаты (

 )
точки
)
точки - встречи линии пересечения плоскостей
ограничений и координатой плоскости
- встречи линии пересечения плоскостей
ограничений и координатой плоскости =
0, - решая систему уравнений:
=
0, - решая систему уравнений:

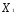 +
+

 =
= ;
;

 +
+

 =
=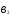 .
.
Поскольку
векторы ( ,
, ),
(
),
( ,
, )
линейно независимы, решение существует
и может быть представлено в виде:
)
линейно независимы, решение существует
и может быть представлено в виде:
 =
=
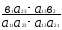 ;
; = 0;
= 0; =
= .
.
Проверяем
выполнение предположения о неотрицательных
объемах производства. Если хотя бы одно
из найденных решений отрицательно, т.е.
 <
0 или
<
0 или <
0, точка
<
0, точка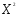 = (
= (

 )
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю,
)
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю, =
0. В противном случае следует найти
значение целевой функции в этой точке:
=
0. В противном случае следует найти
значение целевой функции в этой точке:
 =
=
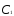
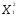 +
+
 .
.
Находим
координаты (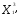
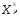
 )
точки
)
точки - встречи линии пересечения плоскостей
ограничений и координатой плоскости
- встречи линии пересечения плоскостей
ограничений и координатой плоскости =
0, решая систему уравнений:
=
0, решая систему уравнений:

 +
+
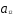
 =
= ;
;

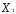 +
+

 =
= .
.
Поскольку
векторы ( ,
, ),
(
),
(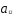 ,
, )
линейно независимы, решение существует
и может быть представлено в виде:
)
линейно независимы, решение существует
и может быть представлено в виде:
 =
=
 ;
; =
= ;
; = 0.
= 0.
Проверяем
выполнение предположения о неотрицательных
объемах производства. Если хотя бы одно
из найденных решений отрицательно, т.е.
 <
0 или
<
0 или <
0, точка
<
0, точка = (
= (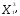

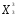 )
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю,
)
не может служить оптимальной
производственной программой предприятия.
В этом случае полагаем доход предприятия
равным нулю, =
0. В противном случае следует найти
значение целевой функции в этой точке:
=
0. В противном случае следует найти
значение целевой функции в этой точке:
 =
=

 +
+
 .
.
Отметим, что приведенные выше выражения для решений систем линейных уравнений, вытекают из теоремы Крамера. При выполнении работы можно воспользоваться любым другим методом решения систем, в том числе методом Гаусса последовательного исключения переменных.
Для нахождения оптимальной производственной программы необходимо из найденных решений выбрать такое, которое обеспечивает наибольший доход предприятию.
Расположим
полученные значения целевой функции
 ,
, ,
,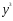 в порядке возрастания 0
в порядке возрастания 0


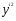

 .
Возможны следующие варианты.
.
Возможны следующие варианты.
Если
 >
> ,
то оптимальной является производственная
программа:
,
то оптимальной является производственная
программа:
( =
=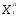 ,
, =
=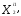
 =
=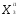 ).
).
Если
 =
= >
> ,
то оптимальной является любая
производственная программа, соответствующая
точкам отрезка, расположенного между
граничными точками
,
то оптимальной является любая
производственная программа, соответствующая
точкам отрезка, расположенного между
граничными точками и
и .
Условимся в этом случае указывать только
два граничных решения:
.
Условимся в этом случае указывать только
два граничных решения:
( =
= ,
, =
=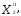
 =
= );
);
(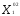 =
=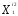 ,
, =
=
 =
= ).
).
Если
 =
= =
= >
0, то также имеется множество оптимальных
производственных программ, позволяющих
предприятию получить одинаковый
наибольший возможный доход. Условимся
в этом случае указывать три граничных
решения (два из которых совпадают):
>
0, то также имеется множество оптимальных
производственных программ, позволяющих
предприятию получить одинаковый
наибольший возможный доход. Условимся
в этом случае указывать три граничных
решения (два из которых совпадают):
( =
= ,
,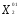 =
=
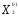 =
= );
);
(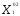 =
= ,
, =
=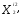
 =
= );
);
( =
= ,
, =
=
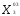 =
= ).
).
По существу задачи оптимизации производственной программы в окончательном решении следует опустить дробную часть (мантиссу) в значениях объемов производства.
В заключении следует рассчитать доход предприятия от реализации оптимальной производственной программы:
 =
=

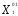 +
+
 +
+
 .
.
