33. Оценка эффективности алгоритмов на бинарном дереве поиска.

Рассмотрим 2 случая:

1-й пусть бинарное дерево полное, тогда не существует пути содержащего более 1+log₂(n) при движении от корня к любому листу => операторы INSERT, MEMBER, DELETE, DELETEMIN имеют время выполнения порядка О(log₂(n)), это означает, что если n будет расти, то время будет расти пропорционально log n.

2-й крайний случай соответствует, когда при заполнении дерева элементы поступаю, например, в порядке возрастания, тогда дерево вырождается в цепочку. В том случае оператор указывает выше время выполнения (в худшем случае О(n)). При заполнении такого дерева на вставку потребуется время такого порядка О(i), а все действия при заполнении n элементами:

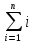= (n*(n+1))/2 => О(n²)

Рассмотрим «средний случай», когда элементы поступают в хранилище в случайном порядке, а точнее при заданном исходном множестве n элементов.

Рассмотрим каков в этом случае порядок времени выполнения основных операторов, введем функцию, аргументы которой являются количеством n элементов в хранилище P(n), возвращая среднее число узлов, которое нужно пройти двигаясь от корня дт какого-то листа.

Составим рекурсивное выражение для функции P(n). Если дерево пустое, то P(0) = 0, если n=1, то Р(1) = 1. Пусть есть n≥2, и пусть 1-м на выход будет элемент «а». Если исходный список отсортировать, то «а» может оказаться на любом месте. Пусть в упорядоченном списке i<a элементов и соответственно (n-i-1)>a, тогда при построении дерева в корне будет элемент «а», т.к он первый перешел, i – потомки левого сына, а (n-i-1) элементов – потомки правого сына.

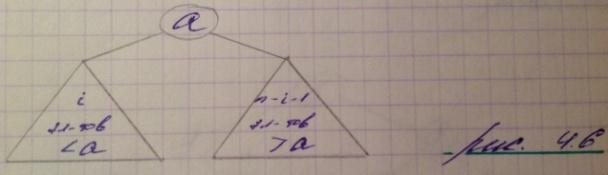
Рис. 4.6

Будем считать, что «а» с равной вероятностью может оказаться на любом месте в упорядоченном списке, т.к любая последовательность i меньших элементов и (n-i-1) больших элементов равновероятны, то среднюю длину путей и в левом, и в правым поддеревьях. Если вершина к исходному дереву, то вычисляя пути от «а» к любому листу мы значениям P(i) и P(n-i-1) должны добавить 1.

P(i)+1 в левой части на рис. 4.6 средняя длина P(i)+1, а в правой P(n-i-1)+1. Отсюда среднюю P(n) можно представить как среднее значение в левой и правой частях дерева рис. 4.6 i/n(P(i)+1)+((n-i-1)/n)*(P(n-i-1)+1). Чтобы окончательно получить среднее значение мы должны передать все n от 0 до (n-1). И мы получим:

P(n) = 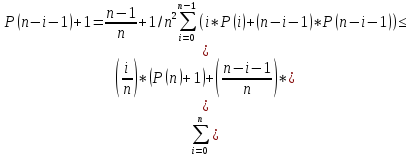(-//-//-//-) (4.1)

Возьмем вторую часть суммы из 4.1 и запишем ее отдельно

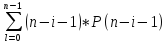
i → n-i-1 результате вся правая часть выражения 4.1 примет вид:

P(n) ≤ 1+2/n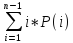^2(4.2)

Выполнится следующее неравенство:

P(n)≤(1+4log₂(n))

n=1

Т.к P(1)=1

n=2 тоже справедливо P(2)=2≤(1+4log₂2)=5.

Предположим, что утверждение выполняется для всех i<n, тогда вместо P(i)в формулу 4.2 получим P(n)≤1+(2/n^2)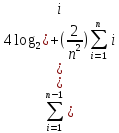. Учтем, что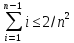=> 2/n^2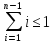, то придем к соотношениюP(n)≤2+(8/n^2)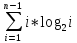(4.3)

Разобьем (4.3) на 2-ве суммы в т. i=[n/2], тогда в 1-й сумме слагаемые не будут превышать i*log₂(n/2), а во 2-й i*log₂(n). В результате получим:

P(n)≤2+(8/n^2)*(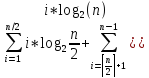(4.4)

При любом четном n 1-я сумма из 4.4 не превышает величины (n^2/8)*log₂(n/2)=(n^2/8)*log₂(n)-(n^2/8). 2-я сумма не будет превышать:

(3*n^2/8)*log₂(n) => по индукции получим нужное нам соотношение:

P(n)≤2+(8/n^2((n^2/2)*log₂(n))-(n^2/8)=1+4*log₂(n) (4.5)

Т.о доказано, что в дереве двоичного поиска, которое получилось путем случайной вставки n элементов средняя длина пути от корня до любого лисьа по произвольному пути имеющем порядок О(log₂(n)),

Более тонкий анализ позволяет указать, что в формуле 4.5 коэффициенты можно заменить на 1.4.

На основе полученного результата можем утверждать, что в среднем время выполнения проверки на принадлежность данного оператора к дереву будет иметь порядок O(log₂(n)), аналогичный порядок будет иметь оператор INSERT, DELETE и DELETEMIN.