Корреляционная зависимость

Попытаемся установить зависимость между этими двумя рядами данных.

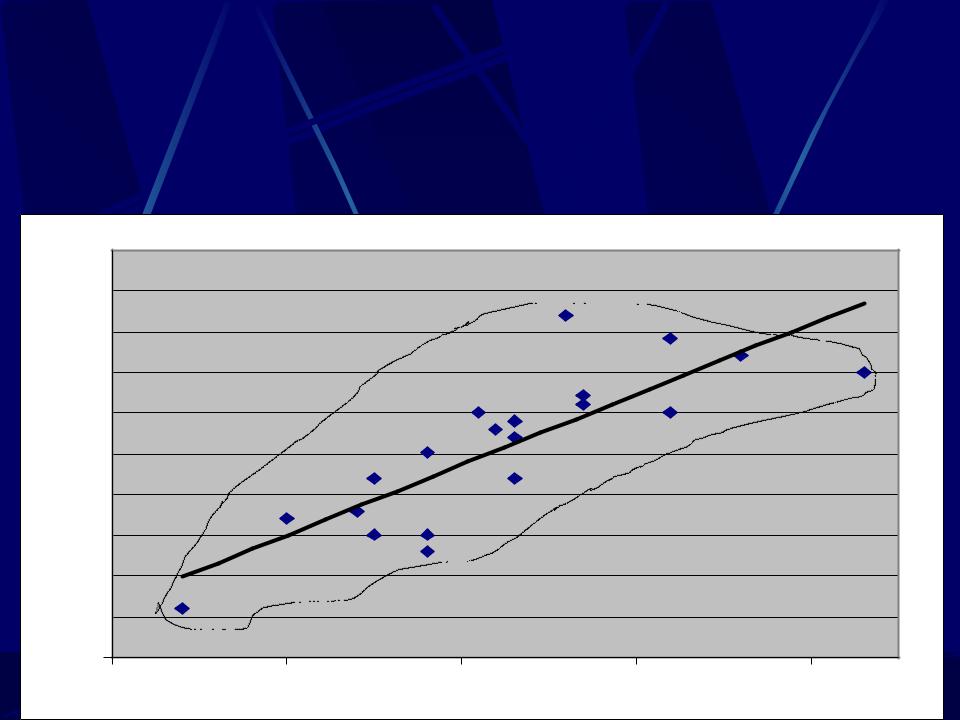
Корреляционная зависимость

Полученные точки лежат внутри некоторой области или «облака», которое обозначено пунктирной линией. Хорошо заметно, что облако вытянуто вдоль какой-то наклонной прямой. Этот факт означает, что величины Х и Y хорошо скоррелированы, т.е. пря увеличении роста вес, как правило, тоже увеличивается. Прямая, вдоль которой вытянулись точки, называется линией регрессии.

Установим уравнение линии регрессии и с его помощью определим, вес курсанта с ростом 195 см.

Корреляционная зависимость

Уравнение искомой прямой имеет вид

y = kx + b, где k = xy – x y

Dx

Здесь x, y и xy - средние значения роста, веса и их попарных произведений,

Dx- дисперсия роста.

Применяя ранее определенные формулы, получаем:

x = 177,35 ; y = 76,65; xy = 13485,15; Dx = 79,1.

Корреляционная зависимость

Подставляя полученные значения в предыдущие формулы, находим k и b :

k 0,87 ; b -78,2 .

Итак, получим следующее уравнение искомой прямой:

y= 0,87x – 78,20.

Она называется эмпирической прямой регрессии.

Подставляя в последнее уравнение x = 195, найдем средний вес курсанта с таким ростом.

Он равен 91 кг.

Коэффициент корреляции

Весьма важной характеристикой при сравнении двух числовых рядов является

коэффициент корреляции, вычисляемый по формуле:

r = xy – x y Sx Sy

Коэффициент корреляции

Коэффициент корреляции играет важную роль в вопросах математической статистики и обладает следующими свойствами:

1.-1 r 1.

2.Если величины Х и Y независимы, то коэффициент корреляции между ними равен

нулю.

3.Если величины Х и Y связаны линейной зависимостью, то коэффициент корреляции равен 1 или -1.

4.Обратно, если коэффициент корреляции равен 1 или -1, то величины Х и Y связаны линейной зависимостью.