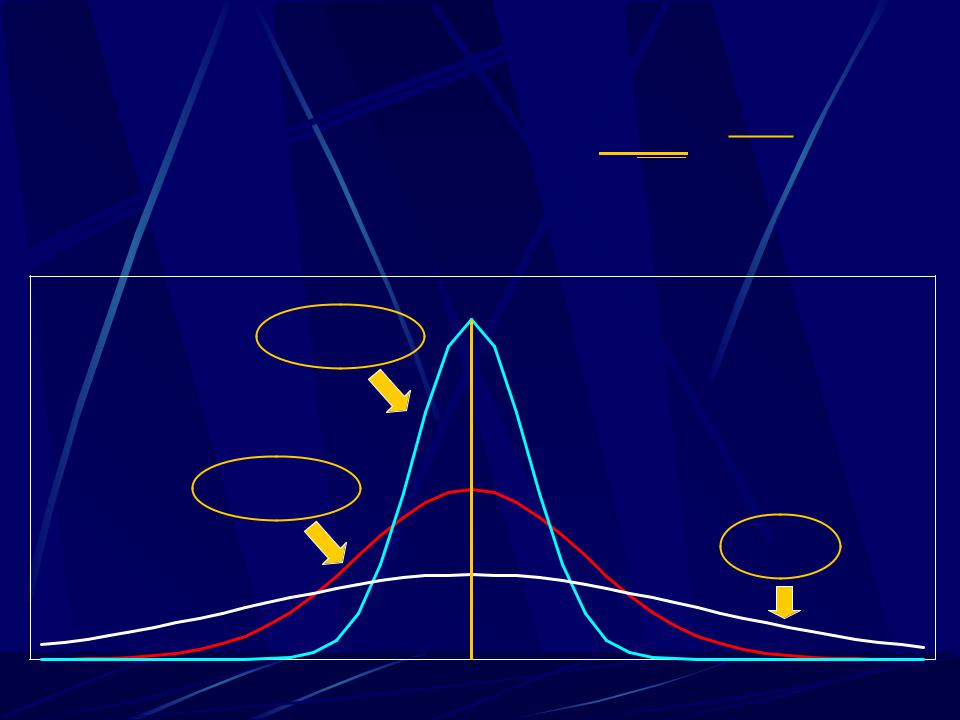
Нормальный закон распределения |
|||
Нормальный закон распределения характеризуется |
|||
плотностью вероятности вида: f(x)= 1 |
(x-m |
)2 |
|
e- 2σ2x |
|
||
где m |
σ 2 |
|
|
– математическое ожидание случайной величины, |
|||
x |
|
|
|
а σ – |
ее среднее квадратическое отклонение. |
|
|
|
σ = |
|
|
|
1/4 |
|
|
|
σ = |
|
|
|
1/2 |
σ = |
|
|
|
1 |
|
|
mx = Mo = |
|
|
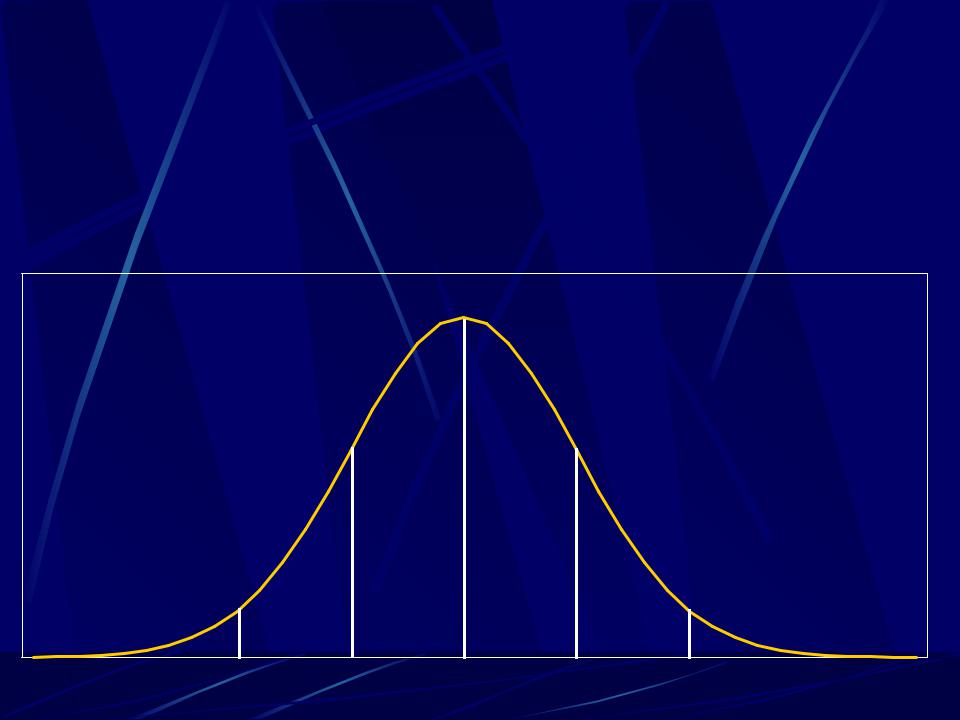
Нормальный закон распределения
Для случайной величины, имеющей нормальный закон распределения справедливы следующие оценки:
вероятность попадания в интервал [- σ, σ] 0,68 ;
вероятность попадания в интервал [- 3 σ, 3 σ]
0,999.
-2 |
- |
mx |
σ 2 |
σ |
σ |
|
σ |
Предмет и задачи |
|
|
|||
математической статистики |
|
||||
Предмет математической статистики |
|||||
составляет |
разработка методов регистрации, |
||||
описания |
и |
анализа |
статистических |
||
экспериментальных данных, |
получаемых |
в |
|||
результате |
наблюдения массовых |
случайных |
|||
явлений. |
|
|
|
|
|
Под статистическими |
данными |
||||
понимается |
некоторая совокупность чисел, |
||||
представляющих |
собой |
количественные |
|||
характеристики |
изучаемых |
процессов |
и |
||
явлений. |
|
|
|
|
|
Предмет и задачи
математической статистики
Задачи математической статистики:
определение закона распределения случайной величины;
проверка правдоподобия гипотез о распределении случайной величины;
нахождение неизвестных параметров распределения.
Основные понятия
математической статистики
Генеральной совокупностью
называется множество числовых значений рассматриваемой количественной характеристики всех исследуемых объектов.
Выборочной совокупностью |
(или просто выборкой) называется |
множество числовых значений |
рассматриваемой количественной |
характеристики для объектов, случайным |
образом отобранных из всей совокупности |
рассматриваемых объектов. |
Основные понятия
математической статистики
Так, например, при исследовании IQ студентов 1-го курса очного отделения юридического факультета генеральной совокупностью является весь списочный состав, а выборочной совокупностью будет совокупность студентов, отобранных для исследования.
Выборка репрезентативна
(представительна), если она достаточно полно представляет изучаемые характеристики генеральной совокупности.
Первичная обработка результатов
эксперимента
Статистические характеристики процессов и явлений получаются при обработке результатов эксперимента по изучению процесса или явления.
Эксперимент мы будем понимать в широком смысле: это может быть натурное испытание некоторого физического объекта, сбор информации о каком-либо процессе или явлении в обществе, наконец, данные для обработки могут быть сгенерированы компьютерной программой, реализующей имитационную модель.
Первичная обработка результатов
эксперимента
Цель обработки результатов - выделить наиболее существенные сведения об интересующем нас процессе или явлении.
Результаты обработки представляют в виде таблиц, графиков, диаграмм и различных числовых характеристик, которые называют параметрами.
Важнейшими из них являются:
среднее арифметическое и дисперсия.
Среднее арифметическое |
|
Пусть x1, x2, ... , xn - некоторые числа. |
|
Их средним арифметическим |
|
- |
называется число |
1 |
|
x = n (x1+ x2+ ... + xn). |
|
Среднее арифметическое
Пример 1. По сведениям автоинспекции, количество дорожных происшествий на улицах города Дрюкова в первую декаду октября было таким:
6, 8, 10, 7, 6, 11, 9, 8, 7,11.
Среднее арифметическое этих чисел, показывающее среднее число дорожных
происшествий в день:
- 1
x =10 (6+8+10+7+6+11+9+8+7+11)=8,3
В сводке за следующие 10 дней такие данные:
0, 5, 7, 7, 12, 11, 14, 13, 7, 6.
Их среднее арифметическое будет:
- 1 (0+5+7+7+12+11+14+13+7+6)=8,2 y = 10