Случайные величины
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Примеры случайных величин:
количество очков, выбитых при одном выстреле в мишень;сумма очков, полученная при бросании двух игральных костей;
число вызовов, поступивших на телефонную станцию за сутки.
Во всех рассмотренных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно затем перечислить.
Случайные величины, принимающие только отделенные друг от друга значения, которые заранее можно перечислить, называются
дискретными случайными величинами.
Случайные величины
Существуют случайные величины другого типа. Например:
величина отклонения точки попадания при выстреле от центра мишени;
вес наугад взятого зерна пшеницы;
рост наудачу выбранного сотрудника некоторой организации.
Возможные значения таких случайных величин не отделены друг от друга: они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще границы неопределенные, расплывчатые
Случайные |
величины, |
возможные значения |
|||
которых |
непрерывно |
заполняют |
некоторый |
||
промежуток, |
называются |
непрерывными |
|||
случайными величинами. |
|
|
|
||
Распределение дискретных случайных
величин
Рассмотрим дискретную случайную величину Х с возможными значениями x1, x2, …, xn. Каждое
из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта величина Х примет одно из этих значений, т. е. произойдет одно из полной группы несовместных событий: {X= x1; X= x2; … X= xn}.
Обозначим вероятности этих событий следующим образом:
Р(X= x1) = р1; Р(X= x2) = р2; … Р(X= xn) = рn.
Распределение дискретных случайных |
||||
Так |
как |
величин |
|
|
рассмотренные несовместные |
||||
события образуют полную группу, то |
|
|||
|
р1 + р2 + … + рn = 1, |
|
||
то есть сумма вероятностей всех возможных |
||||
значений |
случайной |
величины |
равна |
|
единице. |
|
|
|
|
Законом распределения случайной |
||||
величины |
называется всякое соотношение, |
|||
устанавливающее связь между возможными |
||||
значениями |
случайной |
величины |
и |
|
соответствующими им вероятностями. |
|
|||
Распределение дискретных случайных |
|||||||||||||
|
|
|
|
|
|
величин |
|
х, определяющую |
|||||
|
Рассмотрим случайную величину |
||||||||||||
количество очков, выбитых при одном выстреле . Это |
|||||||||||||
дискретная случайная величина, принимающая значения |
|||||||||||||
0, 1, …, 10. Рассмотрим вероятности появления этих очков |
|||||||||||||
для конкретного стрелка и конкретного оружия. |
|
|
|||||||||||
|
|
|
|
|
|
Ряд распределения |
|
|
|
|
|||
xi |
0 |
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 9 10 |
|||
pi |
0.01 |
0.01 |
0.01 0.01 0.01 0.02 0.03 0.04 0.08 0.7 0.08 |
||||||||||
|
0,8 |
Pi |
|
|
Многоугольник распределения |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|||||||||||
Распределение непрерывных |
|
|
случайных величин |
Для непрерывных случайных величин создание |
|
таблицы ряда распределения невозможно, т. к. она должна |
|
содержать бесконечное число столбцов. |
|
Некоторым аналогом многоугольника распределения |
|
можно считать кривую плотности распределения. |
|
f(x) |
Плотность распределения |
|
|
a |
b |
Вероятность попадания случайной величины Х в сегмент |
|
[a,b] равна площади желтой криволинейной трапеции. |
|
Числовые характеристики случайных
величин. Математическое ожидание.
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значенийn .
М[X] = x1p1 + x2p2 + … + xnpn = i=1 xipi
Для непрерывной случайной величины суммирование |
должно быть заменено интегрированием. |
|
М[X] = тx f(x) dx |
- |
Математическое ожидание иногда называют средним |
значением случайной величины. |
Эта характеристика указывает некоторое среднее, |
ориентировочное значение, около которого группируется |
большая часть всех возможных значений случайной |
величины. |
|
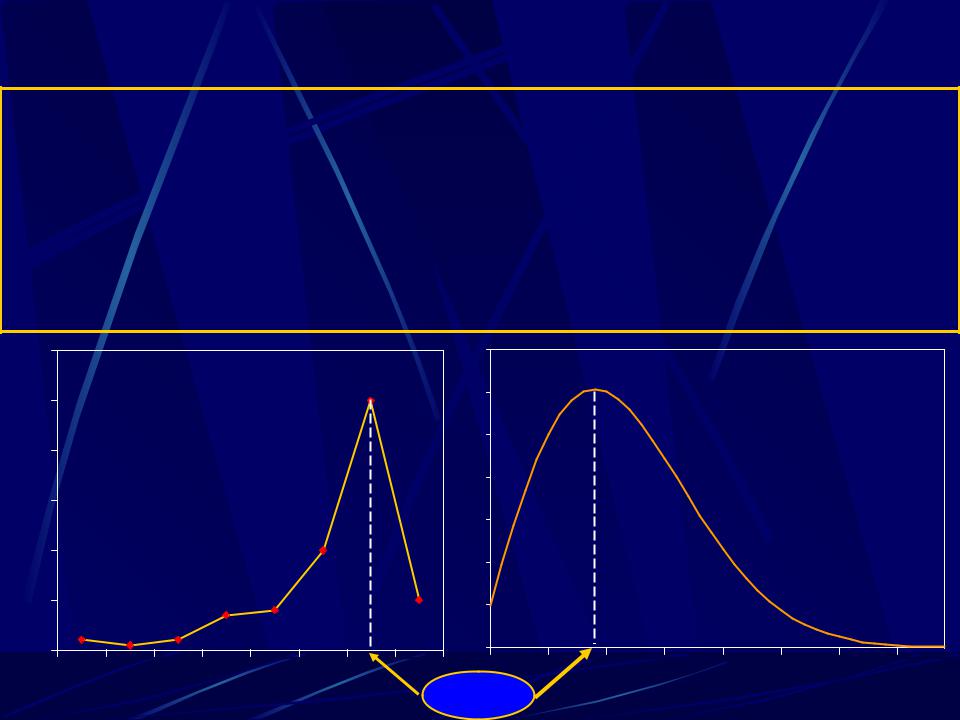
Числовые характеристики случайных |
|
|||||||||||||||
|
|
|
|
|
|
величин. Мода. |
|
|
|
|
|
||||||
|
|
Модой случайной величины ( Mо ) называется ее |
|||||||||||||||
наиболее вероятное значение. |
|
|
|
|
|
|
|
|
|||||||||
|
Термин «наиболее вероятное значение», строго говоря, |
||||||||||||||||
применим только к дискретным величинам. Для |
|||||||||||||||||
непрерывной величины модой является то значение, в |
|||||||||||||||||
котором плотность вероятности максимальна. |
|
|
|
||||||||||||||
0,6 |
Pi |
|
|
|
|
|
|
|
0,7 |
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,5 |
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
M |
|
|
0,10 |
|
M |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
6 |
11 |
16 |
21 |
26 |
31 |
36 |
|
|
|
|
|
|
о |
|
|
|
||||||||
|
|
|
|
|
|
|
|
Мода |
о |
|
|
|
|
|
|
||
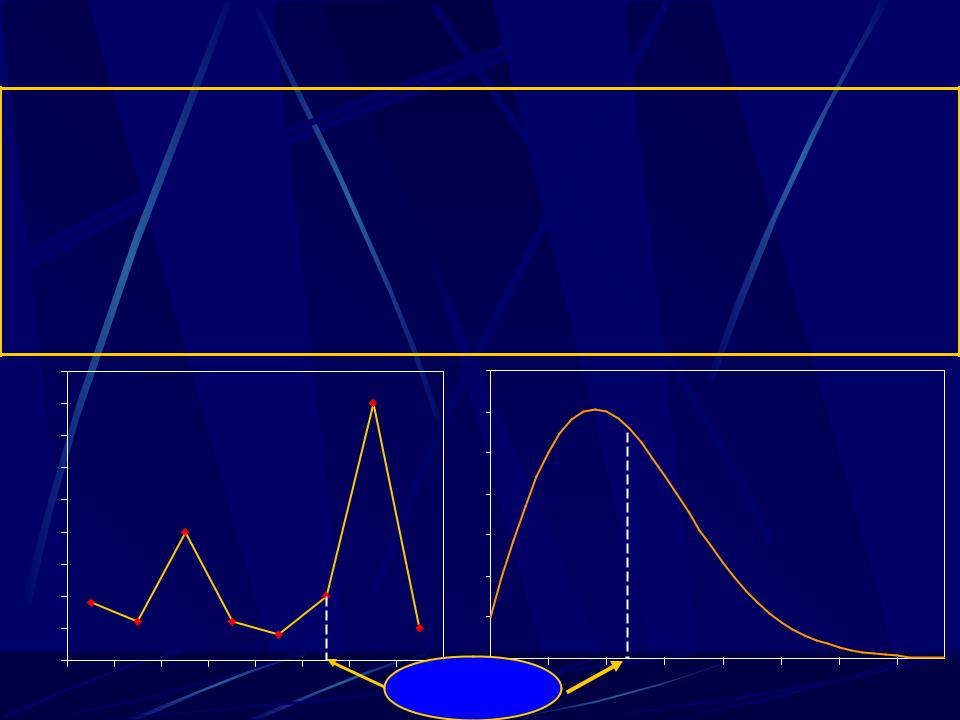
Числовые характеристики случайных |
|
||||||||||
|
|
|
|
величин. Медиана. |
|
|
|
|
|||
Медианой случайной величины называется такое ее |
|||||||||||
значение Me, для которого Р(Х<Me ) = |
Р(Х>Me ), т. е. |
||||||||||
одинаково |
|
вероятно, окажется ли случайная величина |
|||||||||
меньше или больше Me. |
|
|
|
|
|
||||||
Для непрерывной случайной величины медиана – это |
|||||||||||
абсцисса точки, в которой площадь, ограниченная кривой |
|||||||||||
распределения делится пополам. |
|
|
|
|
|
||||||
P |
|
|
|
|
|
0,7 f(x) |
|
|
|
|
|
0,45 i |
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
0,6 |
|
|
|
|
|
0,35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
0,25 |
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
0,3 |
|
|
|
|
|
0,15 |
|
|
|
|
|
0,2 |
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
0,1 |
M |
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
0 |
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6e 7 |
Медиана |
11 e16 |
21 |
26 |
31 |
36 |
Числовые характеристики случайных величин.
Дисперсия и среднее квадратическое отклонение.
Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Обозначим: mx= M(X).
Тогда дисперсия дискретной случайной величины |
||||
вычисляется по формуле: n |
|
– mx)2 |
p |
|
D[X] = x |
i |
|||
i=1 |
i |
|
|
|
Для непрерывной случайной величины формула |
||
вычисления дисперсии примет вид : |
||
|
|
|
|
D[X] = т(x- mx)2 f(x) dx |
|
|
- |
|
Величина, полученная |
извлечением из дисперсии |
|
квадратного корня, называется средним квадратическим |
||
отклонением. |
σ[X]= D[X] |
|
|
||