Элементы теории вероятностей

Лабораторная работа № 2

Цели задания:

1. Повторение основных приемов создания и форматирования таблиц средствами MS Excel .

2. Решение задач по теме «Элементы теории вероятностей. Вероятность суммы и произведения событий»

Подготовка к заданию:

1. Повторить тему «Элементы теории вероятностей» по электронному конспекту, расположенному на сервере по адресу «F:\Методические материалы \ Информационные технологии \ Математика и информатика для юристов».

Состав задания:

1. Решить задачи по теории вероятностей и оформить их решение средствами MS Excel в виде таблиц в соответствии с предложенными ниже образцами. Для вычисления числа вариантов по формулам комбинаторики использовать соответствующие математические функции MS Excel.

Задачи:

1. В лотерее участвует 1000 билетов; из них на один билет выпадает выигрыш 5000 руб., на 10 билетов - выигрыши по 1000 руб., на 50 билетов - выигрыши по 200 руб., на 100 билетов – по 50 руб., остальные билеты невыигрышные. Найти вероятность выиграть не менее 200 руб. при одном купленном билете.

2. Ведутся поиски четырех преступников. Каждый может быть обнаружен в течение суток с вероятностью 0,5. Какова вероятность того, что в течение суток будет обнаружен хотя бы один преступник?

3. Вероятность того, что студент Петров сдаст экзамен по «Истории Отечества», равна 0,7, а вероятность сдачи экзамена по «Математике и информатике» - 0,5. Какова вероятность того, что он успешно сдаст оба экзамена?

4. Имеется 30 одинаковых по форме ручек. 10 из них имееют чернила зеленого цвета, 8 – красного цвета и 12 – синего цвета. Найти вероятность того, что взятая наудачу ручка не будет иметь чернила синего цвета.

5. Два студента юрфака сдают зачет по курсу «Информатика и математика». Вероятность сдачи экзамена первым студентом равна Р(А)=0,6, а вторым Р(В)=0,4. Какова вероятность того, что зачет сдаст хотя бы один студент?

6. Определить вероятность того, что при двух бросках игральной кости хотя бы раз выпадет 6 очков?

7. В урне 6 белых и 4 черных шара. Определить вероятность последовательного извлечения из урны двух белых щаров.

1. Из колоды, содержащей 36 игральных карт, последовательно извлекаются три карты. Какова вероятность того, что:

• все три карты будут трефовой масти?

• все три карты будут тузами?

• это буду туз, король и дама одной масти?

Образцы решения и оформления задач:

Задача 1. Двое стрелков по разу стреляют в мишень. Вероятность попадания при выстреле для первого стрелка равна 0.3, а для второго 0.9. Найти вероятность двух попаданий

Решение. Пусть событие А состоит в том, что мишень поразил 1-й стрелок, а событие В – в том, что мишень поразил второй стрелок. По условию P(A)=0,3 и P(B)=0,9. Событию двух попаданий соответствует произведение событий А·В. По смыслу задачи события А и В являются независимыми, поэтому верна формула Р(АВ)=Р(А)·Р(В).

Оформление задачи в виде таблицы MS Excel приведено ниже.

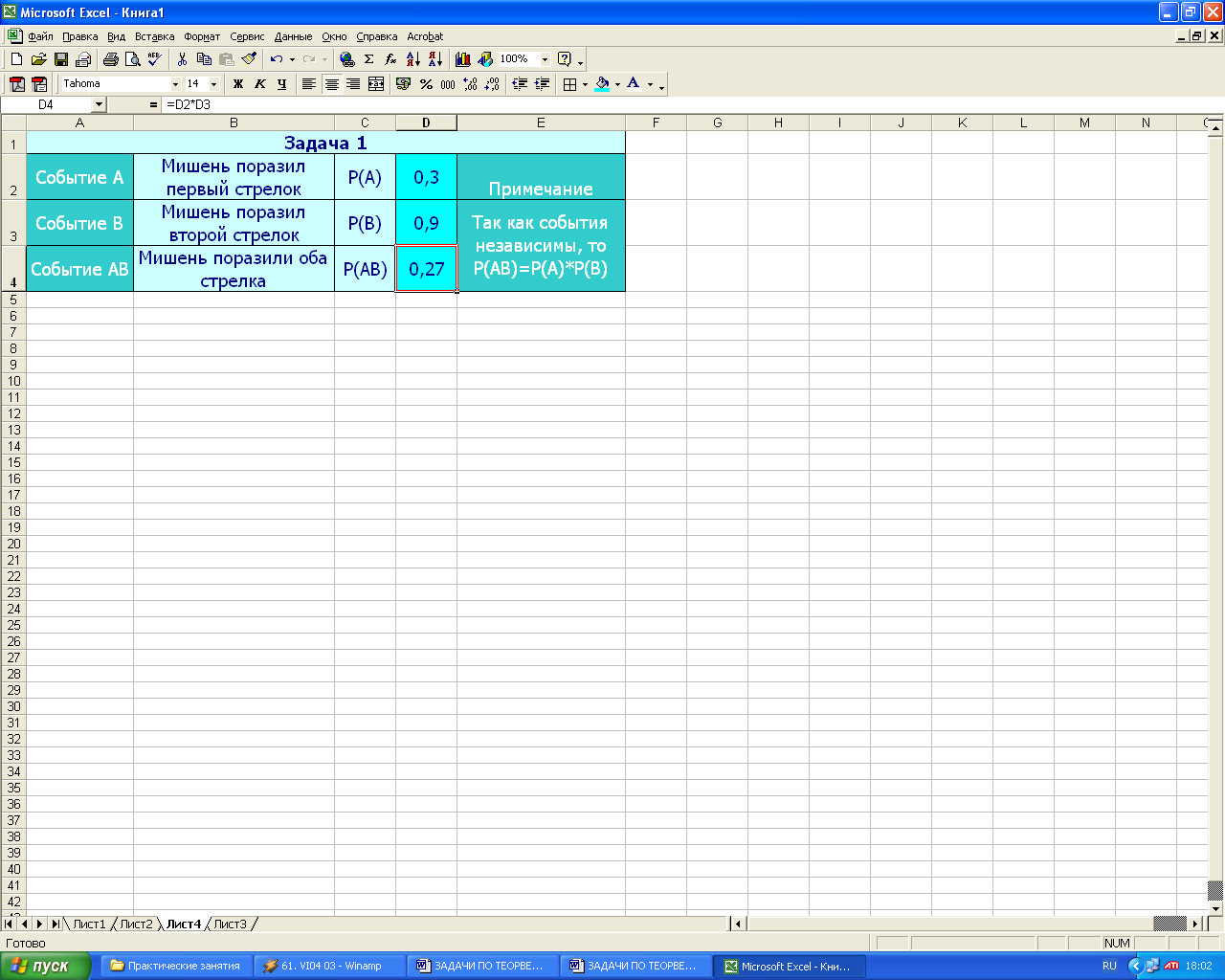
Задача 2. Бросают две игральные кости. Найти вероятность того, что произведение выпавших очков есть четное число.

Решение. Для того чтобы произведение очков было четным, достаточно четности выпавшего числа при любом из бросков. Обозначим через событие А – выпадение четного числа при первом броске, а через событие В выпадение четного числа при втором броске.

Р(А)= Р(В) = 0,5. Нас интересует вероятность события А+ В. Так как эти события являются совместными и независимыми, то

Р(А+В) = Р(А) + Р(В) – Р(АВ)= 0,5 + 0,5 – 0,5 * 0,5 = 1 – 0,25 = 0,75.

Оформление задачи в виде таблицы MS Excel приведено ниже.

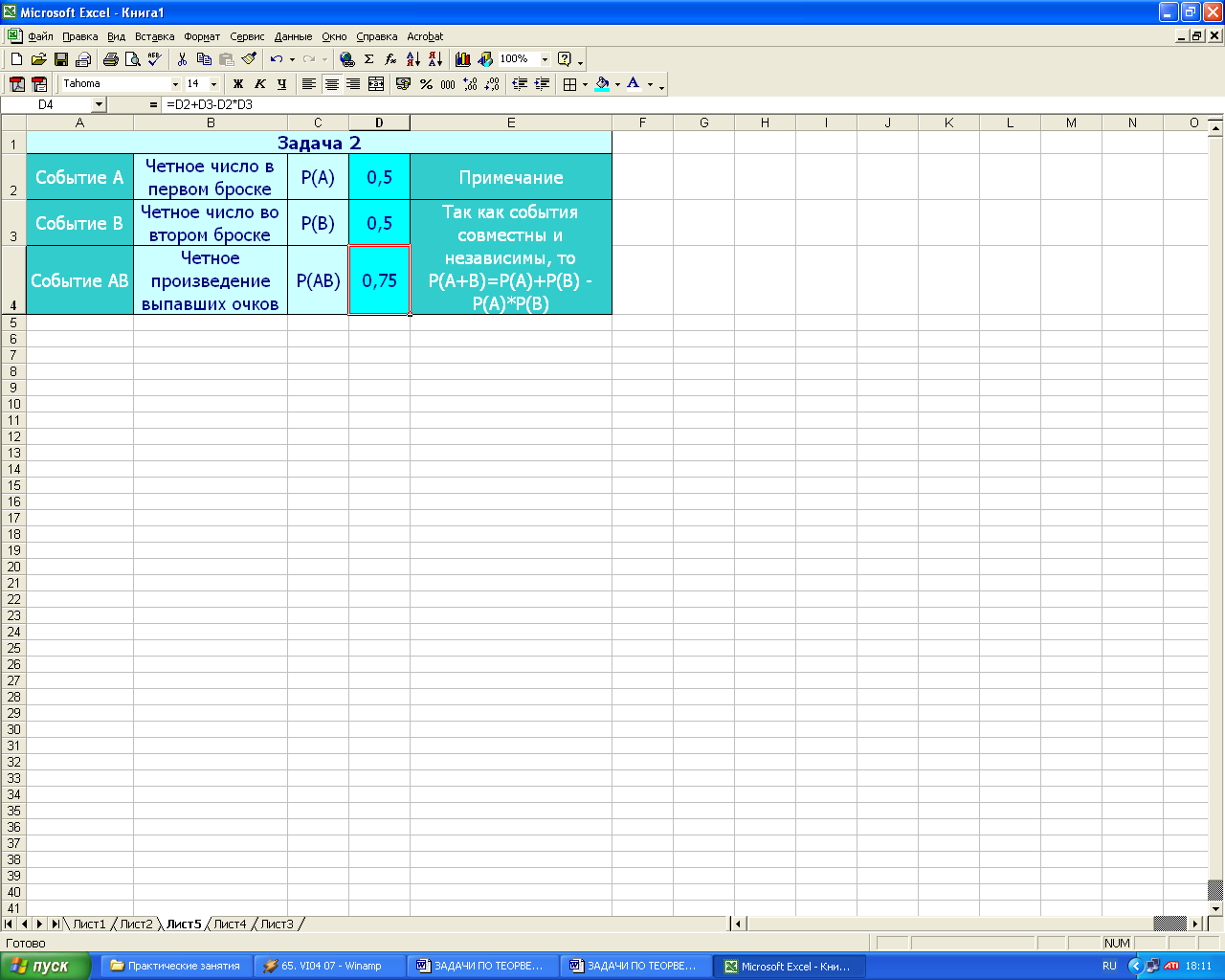
Задача 3. В лототроне 36 пронумерованных по порядку шаров. Определить вероятность того, что оба первых шара будут иметь нечетные номера.

Решение. Обозначим через событие А извлечение первым нечетного шара, а через событие В извлечение вторым нечетного шара. Нас интересует вероятность события АВ. Так как эти события являются зависимыми, то Р(АВ) = Р(А)·Р(В/А).

При этом Р(А) = 1/2, а Р(В/А) = 17/35. Отсюда Р(АВ) = 1/2 * 17/35 = 17/70= 0,24286.

Оформление задачи в виде таблицы MS Excel приведено ниже.