-
Для проверки нулевой гипотезы
при
заданном уровне значимости
выдвинута
конкурирующая гипотеза
.
Тогда область принятия гипотезы может
иметь вид …
-
Соотношением вида
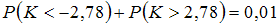можно
определить …
двустороннюю критическую область
-
Левосторонняя критическая область может определяться из соотношения …
-
Если все варианты
исходного
вариационного ряда увеличить в два
раза, то выборочная дисперсия
…
увеличится в четыре раза -
Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
-
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
-
Дан доверительный интервал
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
36,62
-
Дан доверительный интервал
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении объема
выборки этот доверительный интервал
может принять вид …
-
Дан доверительный интервал
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при увеличении надежности
(доверительной вероятности) оценки
доверительный интервал может принять
вид …
-
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
-
Статистическое распределение выборки имеет вид
Тогда
объем выборки равен …
67
-
Статистическое распределение выборки имеет вид
Тогда
значение относительной частоты
равно
…
0,25
-
Из генеральной совокупности извлечена выборка объема
:
Тогда
относительная частота варианты
равна
…0,25 -
Из генеральной совокупности извлечена выборка объема
:
Тогда
выборочная дисперсия равна …0,84 -
Из генеральной совокупности извлечена выборка объема
:
Тогда
несмещенная оценка математического
ожидания равна …13,14 -
Из генеральной совокупности извлечена выборка объема
,
полигон относительных частот которой
имеет вид:
Тогда
число вариант
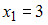в
выборке равно …37 -
Из генеральной совокупности извлечена выборка объема
,
полигон частот которой имеет вид:
Тогда
относительная частота варианты
в
выборке равна …0,05 -
Из генеральной совокупности извлечена выборка объема
,
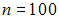гистограмма относительных частот
которой имеет вид
Тогда
значение a
равно …0,11
Абстрактная алгебра
Линейный
оператор
отображает
базис
в
векторы:
;
;
.
Тогда матрица оператора
в
этом базисе имеет вид …
|
|
|
|
|
Прообразом
вектора
при
линейном преобразовании, заданном
матрицей
,
является вектор …
|
|
|
|
|
Образом
вектора
при
линейном преобразовании, заданном
матрицей
,
является вектор …
|
|
|
|
|
Дано
линейное преобразование векторов на
плоскости
,
которое каждый вектор переводит в
сонаправленный вектор, в два раза длиннее
исходного. Тогда матрица
этого
преобразования имеет вид …
|
|
|
|
|
Дано
линейное преобразование векторов на
плоскости
,
которое каждый вектор переводит в вектор
той же длины, но противоположно
направленный исходному. Тогда матрица
этого
преобразования имеет вид …
|
|
|
|
|
Обратным
элементом для матрицы
относительно
операции сложения матриц является …
|
|
|
|
|
Из
заданных операторов пространства
–
пространства трехмерных векторов,
линейным является оператор …
|
|
|
|
|
Коммутативной группой является множество …
|
|
|
|
квадратных матриц с введенной операцией сложения |
На множестве целых чисел группу образует операция * определенная как …
|
|
|
|
|
Коммутативной группой является множество …
|
|
|
|
квадратных матриц с введенной операцией сложения |
Группу по сложению образует множество …
|
|
|
|
целых чисел |
Подгруппой группы невырожденных матриц по умножению является подмножество матриц с …
|
|
|
|
единичным определителем |
Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
|
|
|
четных целых чисел |
Мультипликативная группа рациональных чисел – это множество рациональных чисел …
|
|
|
|
без нуля с операцией умножения |
Множество рациональных чисел с заданной на нем операцией сложения определяет …
|
|
|
|
аддитивную группу |
Для
кольца 
множество
,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
|
|
|
|
абелеву группу |
Бинарной
операцией на множестве векторов в
является
…
|
|
|
|
векторное произведение векторов |
Бинарная
операция, определенная на множестве
,
– это отображение, действующее из
в
множество …
|
|
|
|
|
Бинарная
операция, определенная на множестве
,
– это отображение, действующее из …
|
|
|
|
|
Унарной операцией является …
|
|
|
|
дополнение |
Подалгеброй
алгебры
является
совокупность …
|
|
|
|
|
Подалгеброй
алгебры
является
совокупность …
|
|
|
|
|
Алгебраической операцией является …
|
|
|
|
умножение на множестве рациональных чисел |
Алгеброй является …
|
|
|
|
множество рациональных чисел и операция умножения |
В кольце целых четных чисел единичный элемент …
|
|
|
|
не существует |
Извлечение арифметического корня является алгебраической операцией на множестве …
|
|
|
|
|
={
:
–
вещественное число,
}