Виды алгоритмических конструкций
Для записи алгоритмов существуют разные способы (см. “Способы записи алгоритмов”): текстово-формульная запись, блок-схема, машина Тьюринга, машина Поста, программа на алгоритмическом языке и др. Каждый алгоритм записывается в системе команд исполнителя. Вне зависимости от выбранной формы записи элементарные шаги алгоритма объединяются в алгоритмические конструкции (структуры): последовательные, ветвящиеся, циклические, вспомогательные алгоритмы (см. “Подпрограммы”) и рекурсивные. В 1966 году Бом и Джакопини доказали, что для записи любого сколь угодно сложного алгоритма достаточно трех основных алгоритмических конструкций: последовательных, ветвящихся, циклических.
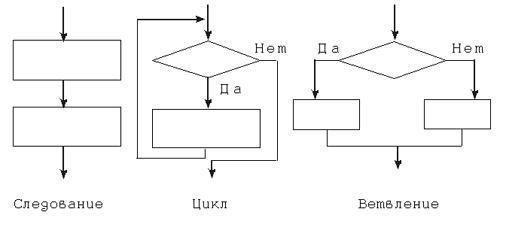
Алгоритм P (или его часть) реализован через последовательную алгоритмическую конструкцию (следование), если каждый шаг алгоритма выполняется один раз, причем после каждого i-го шага выполняется (i + 1)-й шаг, если i-й шаг — не конец алгоритма. Такой алгоритм или часть алгоритма еще называют линейным.
Пример 1. Линейным является алгоритм перевоза через реку Волка, Козы и Капусты, при условии, что в лодке можно перевозить только один из указанных объектов, а на берегу вместе не могут находиться Коза и Волк, а также Коза и Капуста:
1) перевези Козу;
2) вернись на исходный берег;
3) перевези Волка;
4) вернись на исходный берег с Козой;
5) перевези Капусту;
6) вернись на исходный берег;
7) перевези Козу.
Алгоритм P реализован с использованием ветвящейся алгоритмической конструкции (ветвления), если на каком-либо шаге последовательное выполнение алгоритма прерывается, и выбор следующего шага определяется входными данными алгоритма. Ветвление задает выполнение либо одной, либо другой группы операторов в зависимости от выполнения какого-либо условия (в зависимости от истинности или ложности соответствующего логического выражения, см. “Логические выражения”). Затем исполнение алгоритма выходит на общее продолжение. Для конкретных входных данных ветвящаяся алгоритмическая конструкция сводится к последовательной алгоритмической конструкции. Ветвление бывает полным и неполным. В случае неполного ветвления при невыполнении условия никакие действия не выполняются.
Пример 2. Запишем в словесной форме алгоритм решения уравнения ax2 + bx + c = 0, где a, b, c — произвольные действительные числа, а x — искомая величина. Если a 0, то для нахождения корней используются известные формулы, при этом существование корней зависит от знака дискриминанта квадратного уравнения. Если a = 0, то уравнение становится линейным. Однако при b = 0 оно вырождается в равенство c = 0. Поэтому, если c действительно равно 0, то все действительные числа являются корнями такого уравнения, в противном случае — корней нет. Ниже приведена блок-схема данного алгоритма.
Алгоритм P реализован с использованием циклической алгоритмической конструкции, если некая, подряд идущая группа шагов алгоритма, выполняется несколько раз. Количество повторений либо фиксировано, либо зависит от входных данных алгоритма. Любая циклическая алгоритмическая конструкция содержит в себе элементы ветвящейся алгоритмической конструкции: после очередного выполнения группы шагов, входящих в цикл (которое называется шагом цикла, или итерацией), проверяется некоторое условие, формируемое в процессе вычислений. В зависимости от значения этого условия цикл либо завершается, либо начинается выполнение следующего шага цикла.
В качестве примера алгоритма с циклической конструкцией можно рассмотреть алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел (см. “Алгоритм”).
Следование, ветвление и цикл называют базовыми конструкциями структурного программирования. Их особенностью является то, что любая из них имеет только один вход и один выход, поэтому они могут вкладываться друг в друга. Например, цикл может содержать следование из двух ветвлений, каждое из которых включает вложенные циклы.