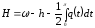2. Метод гельфанда-левитана

В этой главе приведем алгоритм решения обратной задачи методом Гельфанда-Левитана. Метод, в котором используются операторы преобразования, позволяет обратную задачу свести к линейному интегральному уравнению относительно ядра оператора преобразования.

Для описания метода нам потребуется следующая лемма.

Лемма 4.1. Пусть даны числ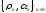а вида

(4.1)

Обозначим

,

(4.2)

где

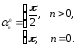
Тогда .

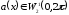Доказательство:

Обозначим 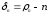. Так как

,

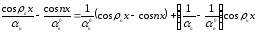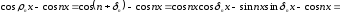
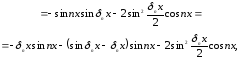
то преобразуем 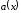к виду

,

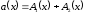где

,

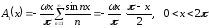(4.3)

Так как

,

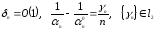то ряды в (4.3) сходятся абсолютно и равномерно на 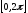, причем 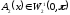. Следовательно, . □

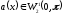Вспомним краевую задачу L=L(q(x), h, H), то есть

Пусть 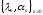- спектральные данные 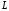, 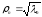. Будем решать обратную задачу восстановления 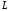по заданным спектральным данным 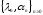. В части 1 было показано, что спектральные данные обладают свойствами:

, где	(4.4)
.	(4.5)

Более точно

,

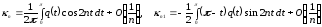то есть главные части зависят линейно от потенциала.

Рассмотрим функцию

,

(4.6)

где

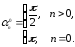
Так как 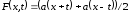, то в силу леммы 4.1 функция 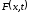является непрерывной, и .

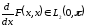Теорема 4.1. При каждом фиксированном 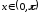ядро 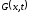из представления (3.11) удовлетворяет линейному интегральному уравнению

(4.7)

Это уравнение называется уравнением Гельфанда-Левитана.

Таким образом, теорема 4.1 позволяет свести нашу обратную задачу к решению уравнения (4.7). Отметим, что (4.7) является интегральным уравнением Фредгольма с параметром .

Доказательство:

Разрешая соотношение (3.11) относительно 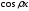, получаем

,

(4.8)

где 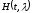- непрерывная функция. Используя (3.11) и (4.8), вычисляем

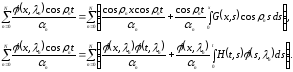
Это дает

,

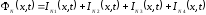где

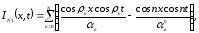
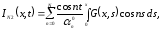
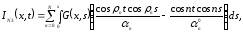
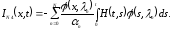
Пусть 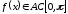, тогда согласно теореме 2.1

.

Кроме того, равномерно по :

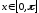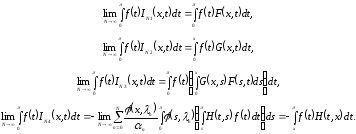
Доопределим 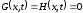при . В силу произвольности 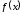приходим к соотношению

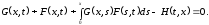
При 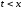это дает (4.7) □

Приведем алгоритм решения обратной задачи.

Алгоритм 4.1.

1. По заданным числам 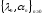строим функцию 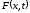по формуле (4.6)

2. Находим функцию 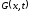из уравнения (4.7)

3. Вычисляем 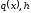и по формулам

,	(4.9)
	(4.10)

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Юрко В. А., Введение в теорию обратных спектральных задач. - Москва, ФМЛ, 2007.

2. Гельфанд И. М., Левитан Б. М., Об определении дифференциального уравнения по его спектральной функции. – Известия АН СССР, сер. матем. 15, 1951, 309-306.

3. Левитан Б. М., Обратные задачи Штурма-Лиувилля. – Москва, Наука, 1984.

4. Марченко В. А., Некоторые вопросы теории линейных дифференциальных операторов второго порядка. - Труды московского математического общества 1, 1952, 327-420.

5. Марченко В. А., Операторы Штурма-Лиувилля и их приложения. – Киев, Наукова Думка, 1977.

6. Levinson N., The inverse Sturm-Liouville problem. – Math. Tidsskr. 13, 1949, 25-30.

7. Привалов И. И., Введение в теорию функций комплексного переменного. – М.: Наука, 1967.

8. Титчмарш Е., Теория функций. – М.: Наука, 1980.

9. Левин Б. Я., Целые функции (курс лекций). – Москва, 1971.

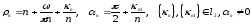
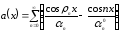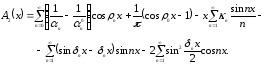
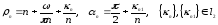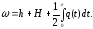
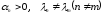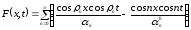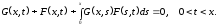
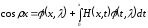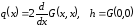48