
- •6. Магнитное поле
- •6.1. Магнитное поле в вакууме
- •6.2. Основные свойства магнитного поля
- •6.3. Силы, действующие на проводник стоком
- •6.4. Магнитное поле в веществе
- •6.4.1. Намагничение вещества, намагниченность
- •6.4.2. Токи намагничивания I′.
- •6.4.3. О расчете поля b в магнетике.
- •6.4.5. Вектор h.
- •2) Связь между векторами j и h.
- •4) Когда внутри магнетика токи намагничивания j′ равны нулю?
- •5) Граничные условия для b и h на границе раздела двух однородных магнетиков.
- •6) Преломление линий вектора b и h
- •7) Ферромагнетики, гистерезис.
6.4.5. Вектор h.
1) Теорема о циркуляции вектора H.
И так мы показали, что в веществе, находящемся в магнитном поле возникают токи намагничивания и, следовательно, циркуляция вектора B определяется не только токами проводимости, но и токами намагничивания и можно записать так (напоминаем – для постоянных токов и полей)
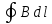 =μο
( I
+ I′),
(6.33)
=μο
( I
+ I′),
(6.33)
Г
где I и I′ – токи проводимости и токи намагничивания, охватываемые заданным контуром Г.
Используя свойство поля вектора J (6.31) выразим I′ через последний, взяв циркуляцию J по тому же контуру Г, тогда:
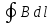 =μο(
I
+
=μο(
I
+
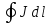 )
или
)
или
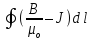 =
I.
(6.34)
=
I.
(6.34)
Величину в скобках, стоящую под знаком интеграла, обозначают как H
H
=
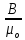 –
J
(6.35)
–
J
(6.35)
и
называют напряженностью
магнитного поля.
Она представляет собой сумму двух
физически разных величин
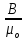 и
J.
Поэтому, как и вектор D
вектор H
– вспомогательный
вектор,
не имеющий какого-то глубокого физического
смысла. Однако его свойство, согласно
(6.34) –
и
J.
Поэтому, как и вектор D
вектор H
– вспомогательный
вектор,
не имеющий какого-то глубокого физического
смысла. Однако его свойство, согласно
(6.34) –
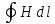 = I,
(6.36)
= I,
(6.36)
оправдывает его введение. Оно говорит, что циркуляция вектора H по произвольному замкнутому контуру Г равна алгебраической сумме токов проводимости I, охватываемых контуром Г – это теорема о циркуляции вектора H. Правило токов здесь, то же, что и в случае циркуляции векторов B и J. Но! Сразу заметим, что, согласно (6.35), вектор H определяется всеми токами, как токами проводимости, так и токами намагничивания.
Необходимо отметить, что соотношения (6.35) и (6.36) справедливы для любых магнетиков, в том числе и анизотропных (о них скажем чуть ниже), кроме того соотношение (6.35) выполняется и для переменных во времени полей.
Из выражения (6.36) видно, что размерность модуля вектора H является ампер на метр (А/м).
Дифференциальная
форма теоремы о циркуляции вектора
H
имеет
вид:
rot
H
= j
или
[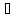 H]
= j
,
(6.37)
H]
= j
,
(6.37)
т.е. ротор вектора H равен плотности тока проводимости в той же точке пространства.
2) Связь между векторами j и h.
Намагниченность вещества принято связывать не с вектором B, с вектором H. Для большого числа магнетиков имеется линейная связь между J и H, а именно:
J = χH , (6.38)
где χ – магнитная восприимчивость вещества, безразмерная величина (т.к. согласно (6.36) размерности J и H одинаковые). Эта характеристика χ для каждого данного магнетика отражает способность вещества намагничиваться в магнитном поле. В отличие от диэлектрической восприимчивости æ, которая всегда положительная, магнитная восприимчивость χ может быть как положительной, так и отрицательной.
Магнетики,
подчиняющиеся зависимости (6.38),
подразделяются на парамагнетики
– у которых χ
невелико
и χ
> 0
и диамагнетики
– у которых χ
< 0.
Соответственно у парамагнетиков J
↑↑
H
, а у диамагнетиков J
↑↓
H.
У диамагнетиков собственные магнитные
моменты молекул очень малы или равны
нулю, так что при наложении магнитного
поля ориентационная намагниченность
магнетика (за счет преимущественной
ориентации собственных магнитных
моментов), по модулю, оказывается меньше
индуцированной (наведенной за счет
гиромагнитного эффекта) намагниченности,
пусть это вектор J′,
который
направлен против поля B
и H,
соответственно. Напомним, что индуцированный
наведенный магнитный момент молекул
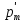 направлен
против
B
и,
соответственно, J′
↑↓
H.
направлен
против
B
и,
соответственно, J′
↑↓
H.
Кроме парамагнетиков и диамагнетиков существуют ферромагнетики, для которых зависимость J (H) имеет сложный характер: она нелинейная и наблюдается гистерезис, т.е. зависимость от предыстории магнетика. Об этих магнетиках мы подробнее поговорим ниже.
3) Связь между B и H.
Эта
связь уже отражена формулой (6.35)
(H
=
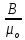 –
J),
которую можно переписать так: B
= μο
(H
+ J)
и
для магнетиков, которые подчиняются
линейной зависимости (6.38)
J
=
χH
в виде:
–
J),
которую можно переписать так: B
= μο
(H
+ J)
и
для магнетиков, которые подчиняются
линейной зависимости (6.38)
J
=
χH
в виде:
B = μο(1+ χ) H = μομH , (6.39)
где величина (1+ χ) = μ (обозначили) – магнитная проницаемость среды:
μ = 1+ χ . (6.40)
Она μ, как и χ характеризует способность вещества намагничиваться в магнитном поле. У парамагнетиков μ > 1, а у диамагнетиков μ < 1, причем как у тех, так и у других μ отличается от единицы весьма мало, т.е. магнитные свойства этих магнетиков выражены очень слабо.
