Теоретическая механика (Кинематика) Ковалев Л.А.

Лекция 3

Краткое содержание: Скорость и ускорение точки в полярных координатах.

Скорость и ускорение точки в полярных координатах

Рассмотрим движение точки в плоскости. В этом случае движение можно задать в полярных координатах. Для этого примем какую-либо точку О плоскости за полюс и проведем из нее полярную ось, например ось Ox. Положение движущейся точки М на плоскости известно, если заданы радиус r и полярный угол  как функции времени, т.е.

и . (3-1)

Эти уравнения называются уравнениями движения точки в полярных координатах. Если из уравнений (3-1) исключить параметр - время t, то получим уравнение траектории в полярных координатах: .

Введем единичный вектор , направленный по радиус-вектору от полюса О к точке М. Тогда .

Д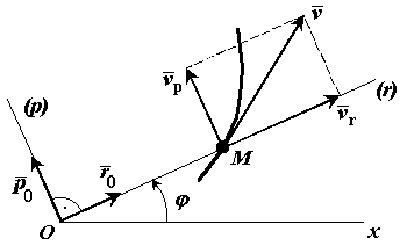ля скорости получаем выра-жение

Производная от единичного вектора по времени равна

(без доказательства)

- единичный вектор,направление которого получается поворотом вектора на 90⁰ в положительном направлении угла  .

После этого для скорости получаем выражение

Это разложение скорости точки на радиальную и трансверсальную (поперечную) составляющие, т.е.

- радиальная скорость; - трансверсальная скорость.

Модуль скорости равен .

Определим ускорение точки

После дифференцирования получаем

Получили разложение ускорения точки на радиальную и трансверсальную (поперечную) составляющие, т.е.

- радиальная скорость;

- трансверсальная скорость.

Модуль ускорения равен .

Частные случаи:

1. Если , то имеем прямолинейное движение по прямой Or .

В этом случае и

2. Если , то имеем движение по окружности .

В этом случае и

- угловая скорость вращения радиус-вектора, - его угловое ускорение.

Скорость и ускорение точки в цилиндрических координатах

При движении точки в пространстве иногда используются цилиндрические оси координат.

Положение точки определяется координатами

, и . (3-2)

2

Лекция 3

12.04.03