Работа и энергия, основные теоремы.

Из залитого подвала, площадь пола которого равна 50 м², требуется выкачать воду на мостовую. Глубина воды в подвале 1,5 м, а расстояние от уровня воды в подвале до мостовой 5 м. Найти работу, которую необходимо затратить для откачки воды. ([1] задача 166)
Оконная штора массой 1 кг и длиной 2 м свертывается на тонкий валик наверху окна. Какая при этом совершается работа? Трением пренебречь. ([1] задача 168)
Два куба с ребром 10 см спаяны гранями и образуют призму; масса куба 1 кг, масса другого 3 кг. Призма стоит на шероховатой горизонтальной плоскости (см. рис.). Подсчитать работу, которую нужно совершить, чтобы опрокинуть через ребро призму, если сила приложена к верхнему основанию призмы перпендикулярно её ребру. Чему будет равна работа если на верху находится тяжёлый куб? ([1] задача 161)

На поверхность Земли с очень большого расстояния падает метеорит. С какой скоростью метеорит упал бы на Землю, если бы атмосфера не тормозила его движения? Считать, что начальная скорость метеорита вдали от Земли равна нулю. ([1] задача 173)
Дают ли возможность результаты решения предыдущей задачи ответить на вопрос: какой должна быть минимальная скорость ракеты, запущенной с поверхности Земли, для того чтобы она преодолела силу земного тяготения и ушла в межпланетное пространство? ([1] задача 174)
Тележка массы скатывается без трения по изогнутым рельсам, имеющим форму, изображенную на рисунке. 1) С какой минимальной высотыдолжна скатиться тележка для того, чтобы она не покинула рельсов по всей их длине? 2) Какие силы действуют на тележку в наивысшей точкепетли? 3) Каково будет движение тележки, если она скатывается с высоты, меньшей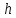? При решении задачи считать колёса тележки малого размера и малой массы и их вращательного движения не рассматривать. ([1] задача 262)

Действуя постоянной силой в 20 кгс, поднимают груз массой в 10 кг на высоту 10 м. Какая при этом совершается работа? Какой потенциальной энергией будет обладать подняты груз? ([1] задача 160)
Коэффициент трения между некоторым телом и плоскостью, наклоненной под 45^о к горизонту, равен 0,2. На какую высоту поднимается это тело, скользя по наклонной плоскости, если ему будет сообщена скорость 10 м/с, направленная вверх вдоль плоскости? Какова будет скорость тела, когда оно вернется в нижнюю исходную точку своего движения? ([1] задача 162)
Идеально упругий шарик движется вверх и вниз в однородном поле тяжести, отражаясь от пола по законам упругого удара. Найти связь между средними по времени значениями его кинетической и потенциальнойэнергий. ([1] задача 186)

Использование законов сохранения энергии и импульса.

Система состоит из двух шариков массами и, соединенных между собой невесомой пружиной с коэффициентом упругости𝓀. Третий шарик с массой , движущийся вдоль оси пружины со скоростью, претерпевает упругое столкновение с шариком, как показано на рисунке. Считая шарики абсолютно жесткими, найти после столкновения: 1) кинетическую энергиюдвижения системы как целого; 2) внутреннюю энергию системы; 3) амплитуду колебания одного шарика относительно другого. До удара система покоилась, а пружина не была деформирована. Какие шарики могут рассматриваться как абсолютно жесткие? ([1] задача 197)
Движущаяся частица претерпевает упругое столкновение с покоящейся частицей такой же массы. Доказать, что после столкновения, если оно не было лобовым, частицы разлетятся под прямым углом друг к другу. Как будут двигаться частицы после лобового столкновения? ([1] задача 206)
Найти изменение кинетической энергии Δи импульса Δтела, движущегося со скоростью, при упругом ударе его о стенку, движущуюся в том же направлении равномерно со скоростью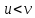. При каком соотношении между скоростью телаи скоростью стенкиударившееся о неё тело остановится? ([1] задача 207)
Космический корабль, движущийся в пространстве, свободном от поля тяготения, должен изменить направление своего движения на противоположное, сохранив скорость по величине. Для этого предлагаются два способа: 1) сначала затормозить корабль, а затем разогнать его до прежней скорости; 2) повернуть, заставив корабль двигаться по дуге окружности, сообщая ему ускорение в поперечном направлении. В каком из этих двух способов потребуется меньшая затрата топлива? Скорость истечения газов относительно корабля считать постоянной и одинаковой в обоих случаях. ([1] задача 247)
Определить коэффициент полезного действия ракеты, т.е. отношение кинетической энергии , приобретённой ракетой, к энергии сгоревшего топлива. Скорость, достигнутая ракетой,= 9 км/с. Теплота сгорания= 4000 ккал/кг, скорость выбрасываемых продуктов сгорания относительно ракеты= 3 км/с. ([1] задача [1] задача 248)
Сферическая капля воды свободно падает в атмосфере перенасыщенного водяного пара. Считая, что скорость возрастания массы капли пропорциональна её поверхности и пренебрегая силами сопротивления среды, определить движение капли. Предполагается, что в момент зарождения капли (= 0) скорость её падения равна нулю. ([1] задача 256)