
Лекция 3
.docxЛекция № 4
Функции нескольких переменных.
Определение 1.
Пусть дано
множество
 .
Обозначим элементы этого множества
через
.
Обозначим элементы этого множества
через
 .
Если каждой точке
.
Если каждой точке
 поставлено в соответствие число
поставлено в соответствие число
 ,
то говорят, что на множестве
,
то говорят, что на множестве
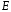 определена функция
определена функция
 переменных. Обозначение
переменных. Обозначение

 .
.
 – область определения
функции;
– область определения
функции;
 – независимые переменные.
– независимые переменные.
Примеры:
 ;
;  .
.
Задача 1. Найти область определения функций;
а)
 ; б)
; б)
 .
.
В дальнейшем мы
будем рассматривать функции двух
переменных
 ,
при этом практически все понятия и
теоремы легко переносятся на случай
функций трех и более переменных.
,
при этом практически все понятия и
теоремы легко переносятся на случай
функций трех и более переменных.
Определение 2.
 – окрестностью точки
– окрестностью точки
 называют круг с центром в точке
называют круг с центром в точке
 и радиусом
и радиусом
 .
.
Обозначение

Определение 3.
Расстоянием
между двумя точками
 и
и
 называется величина
называется величина
 .
.
Определение 4.
Графиком
функции
 переменных называется множество точек
переменных называется множество точек
 пространства
пространства
 .
Для функции двух переменных графиком
является поверхность
.
Для функции двух переменных графиком
является поверхность
 .
.
Для построения
графика функции
 полезно рассматривать функции одной
переменной
полезно рассматривать функции одной
переменной
 и
и
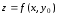 .
Например:
.
Например:
 – эллиптический параболоид.
– эллиптический параболоид.
Определение 5.
Линией уровня
функции
 называется множество точек плоскости,
удовлетворяющих уравнению
называется множество точек плоскости,
удовлетворяющих уравнению
 .
.
Пример 2. Построить линии уровня функции
а)
 ; б)
; б)
 .
.
Определение 6.
Поверхностью
уровня функции
 называется множество точек
называется множество точек
 ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению
 .
.
Пример 3. Построить
поверхности уровня функции
 .
.
Предел функции
 переменных.
переменных.
Определение
(Гейне) Число
 называется пределом функции
называется пределом функции
 в точке
в точке
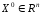 ,
если для любой
последовательности точек
,
если для любой
последовательности точек
 ,
сходящейся к
,
сходящейся к
 ,
числовая последовательность
,
числовая последовательность
 сходится к
сходится к
 .
.
Чтобы доказать,
что функция
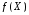 не имеет предела в точке
не имеет предела в точке
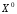 достаточно указать две последовательности
точек
достаточно указать две последовательности
точек
 и
и
 ,
сходящихся к
,
сходящихся к
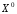 и такие, что
и такие, что
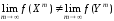 .
.
Пример 4.
 .
Рассмотрим две последовательности
.
Рассмотрим две последовательности
 .
.
Определение
(Коши) Число
 называется пределом функции
называется пределом функции
 в точке
в точке
 ,
если
,
если

 ,
такое, что
,
такое, что

 выполняется неравенство
выполняется неравенство
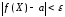 .
.
Обозначение
 ,
, 
Определения Гейне и Коши эквивалентны.
Непрерывность
функции
 переменных.
переменных.
Определение 7.
Функцию
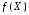 ,
определенную в окрестности точки
,
определенную в окрестности точки
 (и в самой точке), называют непрерывной
в точке
(и в самой точке), называют непрерывной
в точке
 ,
если
,
если
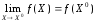 .
.
Точки пространства
 ,
в которых функция
,
в которых функция
 не обладает свойством непрерывности
называются точками разрыва функции.
не обладает свойством непрерывности
называются точками разрыва функции.
Точку
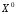 называют точкой разрыва в случае:
называют точкой разрыва в случае:
1)
 определена во всех точках некоторой
окрестности точки
определена во всех точках некоторой
окрестности точки
 ,
кроме самой точки
,
кроме самой точки
 ;
;
2) функция
 определена во всех точках окрестности
определена во всех точках окрестности
 и в самой точке
и в самой точке
 ,
но не существует предела
,
но не существует предела

3) функция
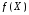 определена во всех точках окрестности
определена во всех точках окрестности
 и в самой точке
и в самой точке
 ,
и существует предел
,
и существует предел
 ,
но
,
но
 .
.
Определение 8.
Функция,
непрерывная в каждой точке множества
 называется непрерывной на множестве
называется непрерывной на множестве
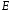 .
.
Свойства непрерывных функций нескольких переменных.
Свойство 1. Если
 и
и
 заданы на одном и том же множестве
заданы на одном и том же множестве
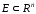 ,
и непрерывны в некоторой точке
,
и непрерывны в некоторой точке
 ,
то функции
,
то функции
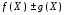 ,
,
 ,
,
 ,
а при условии, что
,
а при условии, что
 и
и
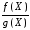 – непрерывны в точке
– непрерывны в точке
 .
.
Свойство 2. Если
функция
 непрерывна на замкнутом ограниченном
множестве
непрерывна на замкнутом ограниченном
множестве
 ,
то:
,
то:
-
она ограничена на этом множестве;
-
она достигает на этом множестве своих наибольшего
 и наименьшего
и наименьшего
 значений;
значений; -
для любого числа
 найдется такая точка
найдется такая точка
 ,
что
,
что
 .
.
Частное и полное приращение функции.
Определение 9.
Полное
приращение функции
 в точке
в точке
 – это функция
– это функция
 .
.
Пусть
 ,
,
 .
.
Обозначим
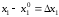 ,
,
 ,…,
,…, .
.
Тогда

Определение 10.
Пусть задана
функция
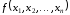 .
Зафиксируем значения
.
Зафиксируем значения
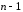 переменной, а одной переменной дадим
приращение
переменной, а одной переменной дадим
приращение
 .
Тогда функция получит частное приращение:
.
Тогда функция получит частное приращение:
 .
.
Замечание Полное
приращение не равно сумме частных
приращений:
 .
.
Дифференциальное исчисление функции нескольких переменных.
Определение 1.
Пусть у
функции
 переменная
переменная
 зафиксирована, а переменная
зафиксирована, а переменная
 получает приращение
получает приращение
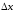 .
Тогда приращение функции будет
.
Тогда приращение функции будет
 .
.
Если существует
предел
 ,
то его называют частной производной от
функции
,
то его называют частной производной от
функции
 в точке
в точке
 по переменной
по переменной
 и обозначают:
и обозначают:
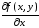 или
или
 ,
или
,
или
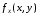 .
.
Аналогично
определяется частная производная по
переменной

При нахождении
частной производной применимы все
формулы и правила дифференцирования
функции одной переменной, так как по
определению мы фиксируем все переменные,
кроме одной, и фактически имеем дело с
функцией одной переменой. Если, например,
находим производную по
 ,
то все остальные аргументы рассматриваем
как константы.
,
то все остальные аргументы рассматриваем
как константы.
Пример 5.
Найти частные
производные функции
 .
.
Решение.
При нахождении
 считаем,
что
считаем,
что
 – константа, а
– константа, а
 – переменная
величина, поэтому
– переменная
величина, поэтому
 .
Аналогично,
.
Аналогично,
 .
.
Пример 6. Найти частные производные функции
 .
.
Решение.
Находим
 ,
считая, что
,
считая, что
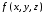 – функция одного аргумента –
– функция одного аргумента –
 ,
а
,
а
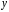 и
и
 – константы:
– константы:
 .
.
Замечание.
Для функции многих переменных из
существования конечных частных
производных в точке
 не следует непрерывность функции в этой
точке.
не следует непрерывность функции в этой
точке.
Дифференциал функции нескольких переменных.
Определение.
Если приращение функции
 в точке
в точке
 можно записать в виде
можно записать в виде
 ,
где
,
где
 и
и
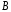 зависят только от
зависят только от
 и
и
 ,
и не зависят от
,
и не зависят от
 ,
,
 ,
то функция называется дифференцируемой
в точке
,
то функция называется дифференцируемой
в точке
 .
.
Выражение
 называется дифференциалом функции
называется дифференциалом функции
 в точке
в точке
 и обозначается символом
и обозначается символом
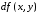 .
.
Теорема.
Если функция
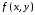 дифференцируема в точке
дифференцируема в точке
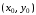 ,
то она имеет в этой точке частные
производные, причем
,
то она имеет в этой точке частные
производные, причем
 .
.
Дифференциал
функции
 переменных записывается аналогично:
переменных записывается аналогично:
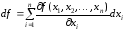 .
.
Теорема (достаточное
условие дифференцируемости)
Если функция
 имеет в точке
имеет в точке
 непрерывные частные производные, то
она дифференцируема в этой точке.
непрерывные частные производные, то
она дифференцируема в этой точке.
Утверждение.
Функция
 ,
дифференцируемая в точке
,
дифференцируемая в точке
 ,
является непрерывной в этой точке.
,
является непрерывной в этой точке.
Дифференцирование сложной функции.
1. Случай
одной независимой переменной.
Если
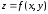 дифференцируемая функция аргументов
дифференцируемая функция аргументов
 и
и
 ,
которые в свою очередь являются
дифференцируемыми функциями независимой
переменной
,
которые в свою очередь являются
дифференцируемыми функциями независимой
переменной
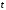 :
:
 ;
;
 ,
то производная сложной функции
,
то производная сложной функции
 может быть вычислена по формуле
может быть вычислена по формуле
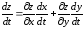 , (*)
, (*)
которая называется формулой полной производной.
В частности, если
 совпадает с одним из аргументов, например
совпадает с одним из аргументов, например
 ,
то «полная» производная
,
то «полная» производная
 по
по
 будет
будет

Пример 7. Найти
 ,
если
,
если
 ,
где
,
где
 ,
,
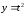 .
.
Решение.

 .
.
Пример 8. Найти
частную производную
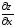 и полную производную
и полную производную
 ,
если
,
если
 ,
где
,
где
 .
.
-
Случай нескольких независимых переменных. Если
 сложная функция нескольких независимых
переменных, например
сложная функция нескольких независимых
переменных, например
 ,
где
,
где
 ;
;
 (
( и
и
 – независимые переменные;
– независимые переменные;
 ,
,
 и
и
 – дифференцируемые функции), то частные
производные
– дифференцируемые функции), то частные
производные
 по
по
 и
и
 выражаются так:
выражаются так:
 ;
;  .
.
Во всех рассмотренных случаях справедлива формула
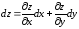
(свойство инвариантности первого дифференциала).
Пример 9.
Найти
 ,
если
,
если
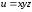 ,
где
,
где
 ,
,
 ,
,
 .
.
Пример 10. Показать,
что функция
 удовлетворяет уравнению
удовлетворяет уравнению
 .
.
Решение. Обозначим
 .
Тогда
.
Тогда
 ,
,  .
.
Подставив частные производные в левую часть уравнения, будем иметь
 Пример
11. Найти
Пример
11. Найти
 и
и
 ,
если
,
если
 ,
где
,
где
 ,
,
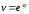 .
.
