
Лекция 5
.docxЛекция № 6-7
Производная по направлению. Градиент.
Пусть функция
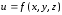 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
 и дифференцируема в
и дифференцируема в
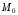 .
.
Рассмотрим
всевозможные лучи, выходящие из
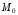 .
Каждый луч задается единичным вектором
.
Каждый луч задается единичным вектором
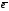 с координатами
с координатами
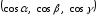 и определяет некоторое направление.
и определяет некоторое направление.
Фиксируем луч,
выходящий из точки
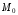 .
На прямой, содержащей этот луч, возьмем
точку
.
На прямой, содержащей этот луч, возьмем
точку
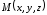 и рассмотрим вектор
и рассмотрим вектор
 .
Так как
.
Так как
 ,
то
,
то
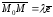 ,
или
,
или
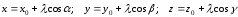 . (1)
. (1)
Равенство (1)
показывает, что на прямой, проходящей
через точку
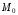 и определяемой вектором
и определяемой вектором
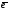 ,
функция
,
функция
 представляет собой сложную функцию
одной переменной
представляет собой сложную функцию
одной переменной
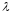 .
.
Определение.
Производную указанной сложной функции
по переменной
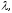 взятую в точке
взятую в точке
 ,
называют производной функции
,
называют производной функции
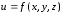 в точке
в точке
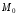 по направлению, определяемому единичным
вектором
по направлению, определяемому единичным
вектором
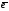 .
.
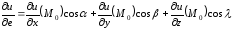 .
(2)
.
(2)
Определение.
Градиентом функции
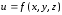 в данной точке
в данной точке
 называется вектор, координаты которого
имеют вид
называется вектор, координаты которого
имеют вид
 ,
,
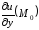 ,
,
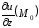 .
.
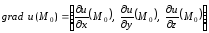 . (3)
. (3)
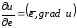 . (4)
. (4)
Производная функции
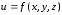 в точке
в точке
 по направлению, определяемому градиентом
этой функции, имеет максимальное значение
по сравнению с производной в этой точке
по любому другому направлению. Значение
производной функции
по направлению, определяемому градиентом
этой функции, имеет максимальное значение
по сравнению с производной в этой точке
по любому другому направлению. Значение
производной функции
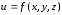 по направлению, определенному градиентом
этой функции в данной точке равно
по направлению, определенному градиентом
этой функции в данной точке равно
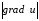 .
.
 .
.
Таким образом, направление градиента – направление быстрейшего роста функции; противоположное направление – направление быстрейшего уменьшения функции. Направления, перпендикулярные к направлению градиента – направления постоянства функции.
Для функции
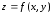 направление градиента перпендикулярно
линиям уровня.
направление градиента перпендикулярно
линиям уровня.
Для функции
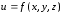 направление градиента перпендикулярно
поверхностям уровня.
направление градиента перпендикулярно
поверхностям уровня.
Если градиент
функции находится не в фиксированной
точке
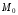 ,
то этот вектор называется полем градиента
функции
,
то этот вектор называется полем градиента
функции
 .
.
Пример 1.
Дана функция
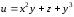 .
Найти
.
Найти
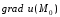 и
и
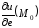 ,
где
,
где
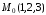 ;
;
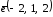 .
.
Касательная плоскость и нормаль к поверхности.
1. Уравнение касательной плоскости и нормали для случая явного задания поверхности.
Определение.
Касательной плоскостью к поверхности
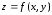 в точке
в точке
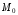 (точка
касания) называется плоскость, в которой
лежат все касательные в точке
(точка
касания) называется плоскость, в которой
лежат все касательные в точке
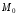 к различным кривым, проведенным на
поверхности через эту точку.
к различным кривым, проведенным на
поверхности через эту точку.
Определение. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания.
Если
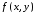 – дифференцируемая функция, то уравнение
касательной плоскости
в точке
– дифференцируемая функция, то уравнение
касательной плоскости
в точке
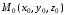 поверхности имеет вид
поверхности имеет вид
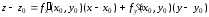 (5)
(5)
Уравнения нормали имеют вид
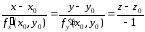 . (6)
. (6)
Пример 2.
Найти уравнения касательной плоскости
и нормали к поверхности
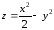 в точке
в точке
 .
.
2. Уравнение касательной плоскости и нормали для случая неявного задания поверхности.
Пусть уравнение
гладкой поверхности задано в неявной
форме
 и
и
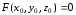 .
Тогда соответствующие уравнения будут
иметь такой вид:
.
Тогда соответствующие уравнения будут
иметь такой вид:
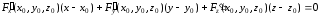
– уравнение касательной плоскости и
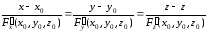 .
.
– уравнение нормали к поверхности.
Пример 3.
Написать уравнение касательной плоскости
и нормали к поверхности
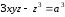 в точке, для которой
в точке, для которой
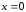 ,
,
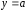 .
.
Решение.
Найдем аппликату точки касания, подставив
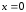 и
и
 в уравнение поверхности:
в уравнение поверхности:
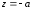 .
Таким образом, точка касания
.
Таким образом, точка касания
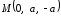 .
.
Замена переменных
При рассмотрении выражений, содержащих функции и их производные, часто оказывается целесообразным перейти к другим независимым переменным. Иногда необходимо перейти не только к новым переменным, но и к новым функциям, которые связаны с исходными переменными и функциями определёнными соотношениями. При замене переменной используются правила дифференцирования сложных и неявно заданных функций.
-
Замена переменных в выражении, содержащем обыкновенные производные.
Пусть в дифференциальном
выражении
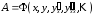 требуется перейти к новым переменным:
требуется перейти к новым переменным:
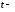 независимой
переменной и
независимой
переменной и
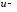 функции,
связанным с прежними переменными
функции,
связанным с прежними переменными
 и
и
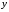 уравнениями
уравнениями
 . (7)
. (7)
Дифференцируя уравнение (7), будем иметь:
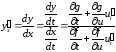 .
.
Аналогично выражаются высшие производные. В результате мы получаем
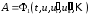 .
.
Пример 3.
Преобразовать уравнение
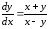 перейдя к полярным координатам
перейдя к полярным координатам
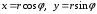 .
.
Решение.
Рассматривая
 как функцию
как функцию
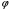 ,
получим
,
получим
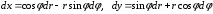 ,
,
отсюда
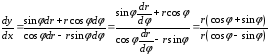 ,
,
или после упрощений
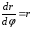 .
.
Пример 4.
Преобразовать уравнение
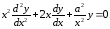 ,
полагая
,
полагая
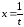
Решение.
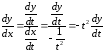 ,
,
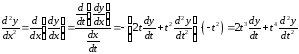 .
.
Подставляем в уравнение
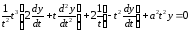 или
или
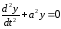 .
.
Пример 5.
Преобразовать
уравнение
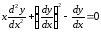 ,
приняв
,
приняв
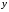 за аргумент, а
за аргумент, а
 за функцию.
за функцию.
Решение.
 ,
, 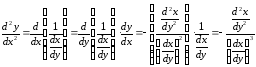 .
.
Подставим эти выражения производных в данное уравнение, будем иметь
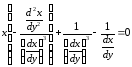 ,
или окончательно
,
или окончательно
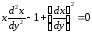 .
.
-
Замена независимых переменных в выражении, содержащем частные производные.
Если в дифференциальном выражении
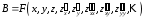
положить  , (8)
, (8)
где
 и
и
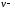 новые
независимые переменные, то частные
производные
новые
независимые переменные, то частные
производные
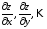 определяются из следующих уравнений:
определяются из следующих уравнений:
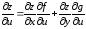 ,
,  .
.
Пример 6.
Уравнение колебаний струны
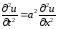 преобразовать к новым независимым
переменным
преобразовать к новым независимым
переменным
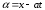 и
и
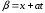 .
.
Решение.
Выразим частные производные от
 по
по
 и
и
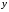 через частные производные от
через частные производные от
 по
по
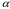 и
и
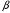 .
.
Очевидно,
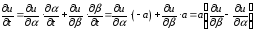 ,
,
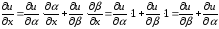 .
.
Дифференцируем вторично, применяя ту же формулу
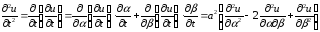 ,
,
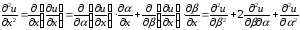 .
.
Подставив в
уравнение, получим
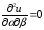
Пример 7.
Преобразовать
уравнение
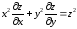 ,
приняв за новые независимые переменные
,
приняв за новые независимые переменные
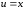 ,
,
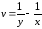 и за новую функцию
и за новую функцию
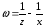 .
.
Решение.
Выразим частные производные
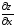 и
и
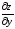 через частные производные
через частные производные
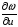 и
и
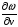 .
Для этого продифференцируем данные
соотношения между старыми и новыми
переменными:
.
Для этого продифференцируем данные
соотношения между старыми и новыми
переменными:
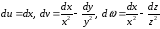 .
.
С другой стороны,
 .
.
Поэтому
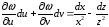
или
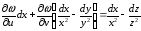 .
.
Отсюда
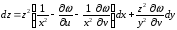
и, следовательно,
 и
и
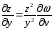 .
.
Подставляя эти выражения в данное уравнение, получим
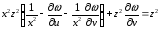 или
или 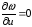 .
.
Формула Тейлора
Сначала рассмотрим
функцию двух переменных
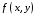 .
Предполагаем, что в некоторой окрестности
точки
.
Предполагаем, что в некоторой окрестности
точки
 существуют все частные производные
функции
существуют все частные производные
функции
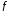 до
до
 -го
порядка включительно. Фиксируем
-го
порядка включительно. Фиксируем
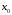 ,
,
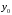 .
Запишем
.
Запишем
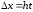 ,
,
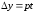 ,
тогда значение функции в точке
,
тогда значение функции в точке
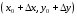 запишется как
запишется как
 .
Фиксируем
.
Фиксируем
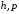 и будем считать, что меняется только
и будем считать, что меняется только
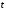 ,
тогда
,
тогда
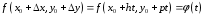 .
.
Применим
к функции
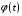 формулу Маклорена с остаточным членом
в форму Пеано:
формулу Маклорена с остаточным членом
в форму Пеано:
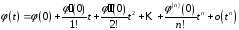
В
соответствии с нашими обозначениями
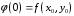 .
Вычислим производные функции
.
Вычислим производные функции
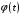 через производные функции
через производные функции
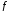 :
:
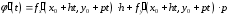 ,
,
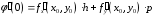 ,
,
аналогично
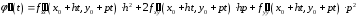 ,
,
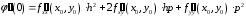 ,
,
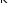
Легко проверить,
что
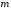 -я
производная имеет вид
-я
производная имеет вид
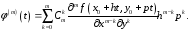
Подставив все это
в формулу Маклорена для
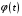 и вернувшись к обозначениям
и вернувшись к обозначениям
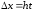 ,
,
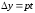 ,
мы получим
,
мы получим
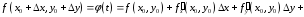
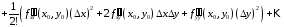
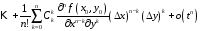 .
.
Обозначим теперь
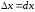 ,
,
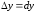 ,
,
 .
.
Так как
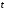 и
и
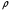 отличаются постоянным множителем, то
отличаются постоянным множителем, то
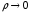 при
при
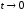 и наоборот, а также
и наоборот, а также
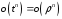 (при
(при
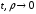 ).
Тогда полученная нами формула Тейлора
для функции двух переменных может быть
записана в следующем виде:
).
Тогда полученная нами формула Тейлора
для функции двух переменных может быть
записана в следующем виде:
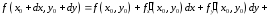
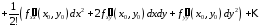
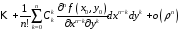
или
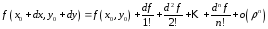 ,
,
где
все дифференциалы берутся в точке
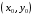 .
.
